Cauchy's functional equation
|
Read other articles:

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

1984 song by Twisted Sister The PriceSingle by Twisted Sisterfrom the album Stay Hungry B-sideS.M.F.ReleasedDecember 1984Length3:48LabelAtlanticSongwriter(s)Dee SniderProducer(s)Tom WermanTwisted Sister singles chronology I Wanna Rock (1984) The Price (1984) Shoot 'Em Down (1985) Music videoThe Price on YouTube The Price is a song by American heavy metal band Twisted Sister, released in 1984 as the third and final single from their third studio album, Stay Hungry. The song was written by Dee ...
Ini adalah nama Korea; marganya adalah Moon. Joo WonLahirMoon Jun-won30 September 1987 (umur 36)SeoulPendidikanSekolah Seni (Teater) Universitas Sungkyunkwan (Film dan Televisi) Sekolah Pascasarjana Komunikasi Massa di Universitas KonkukPekerjaanAktorTahun aktif2007-sekarangAgenSim EntertainmentTinggi185 cm (6 ft 1 in)Nama KoreaHangul주원 Hanja周元 Alih AksaraJu-wonMcCune–ReischauerChu-wŏnNama lahirHangul문준원 Hanja文晙原 Alih AksaraMun Jun-wonMcCune–R...

Untuk kegunaan lain, lihat Gereja Katolik Lama (disambiguasi). Katedral St. Gertrude di Utrecht. Tahta Uskup Agung Utrecht dan gereja induk dari Gereja Katolik Lama Bagian dari seri tentangKekristenan YesusKristus Yesus menurut Kristen Lahir Kiprah Wafat Kebangkitan Kenaikan AlkitabDasar Perjanjian Lama Perjanjian Baru Injil Kanon Gereja Syahadat Perjanjian Baru dalam Kitab Yeremia Teologi Allah Tritunggal Bapa Anak/Putra Roh Kudus Apologetika Baptisan Kristologi Sejarah teologi Misi Keselama...

У этого термина существуют и другие значения, см. Америго Веспуччи (значения). Америго Веспуччиитал. Amerigo Vespucci Дата рождения 9 марта 1454(1454-03-09) Место рождения Флоренция, Флорентийская республика Дата смерти 22 февраля 1512(1512-02-22) (57 лет) Место смерти Севилья, Испания Гра...

Melayu CocosPengantin Melayu dalam acara pernikahan di Kepulauan Cocos (Keeling), 1912.Daerah dengan populasi signifikan Malaysia 4.000[1] Kepulauan Cocos (Keeling) 400BahasaMelayu Cocos, Inggris, MalaysiaAgamaIslamKelompok etnik terkaitJawa, Betawi, Sunda Melayu Cocos adalah sekelompok masyarakat asli/lokal yang berbudaya Melayu yang membentuk mayoritas penduduk Kepulauan Cocos (Keeling), yang sekarang merupakan bagian wilayah/teritori dari negara Australia. Meskipun merek...

American baseball player (1938–2022) Baseball player Bob LockerLocker in 1973PitcherBorn: (1938-03-15)March 15, 1938George, Iowa, U.S.Died: August 15, 2022(2022-08-15) (aged 84)Bozeman, Montana, U.S.Batted: SwitchThrew: RightMLB debutApril 14, 1965, for the Chicago White SoxLast MLB appearanceJune 20, 1975, for the Chicago CubsMLB statisticsWin–loss record57–39Earned run average2.75Strikeouts577Saves95 Teams Chicago White Sox (1965–1969) Seattle Pilo...

Keuskupan RagusaDioecesis RagusiensisKatolik Katedral RagusaLokasiNegaraItaliaProvinsi gerejawiSiracusaStatistikLuas1.029 km2 (397 sq mi)Populasi- Total- Katolik(per 2014)222.756214,913 (96.5%)Paroki71Imam102 (diosesan)27 (Ordo Relijius)8 Deakon PermanenInformasiDenominasiGereja KatolikRitusRitus RomaPendirian1 Oktober 1955KatedralCattedrale di San GiovanniKepemimpinan kiniPausFransiskusUskup AgungCarmelo CuttittoPetaSitus webwww.diocesidiragusa.it Keuskupan...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

Fairbanks-MorseStato Stati Uniti Fondazione1871 a Chicago Fondata daThaddeus FairbanksCharles Hosmer Morse Chiusura1958 ( fusa con Penn-Western in Fairbanks Whitney Corporation) Sede principaleChicago SettoreMeccanica Prodottidispositivi di pesatura, pompe, motori, mulini a vento, locomotive ferroviarie, forniture industriali Modifica dati su Wikidata · Manuale Fairbanks-Morse (and Company) era una impresa industriale americana produttrice di una vasta gamma di apparecchiature ...

Faroese politician and footballer Páll á ReynatúgvuPáll á Reynatúgvu in 2012.Member of the LøgtingIncumbentAssumed office 1998Minister of Health and Social AffairsIn office2002–2004Speaker of the LøgtingIn office2015–2019 Personal detailsBorn (1967-07-26) 26 July 1967 (age 56)TórshavnPolitical partyRepublicAssociation football careerPosition(s) MidfielderSenior career*Years Team Apps (Gls)1987–2003 B71 Sandur 224 (55)International career1993 Faroe Islands 5 (0) *Club d...
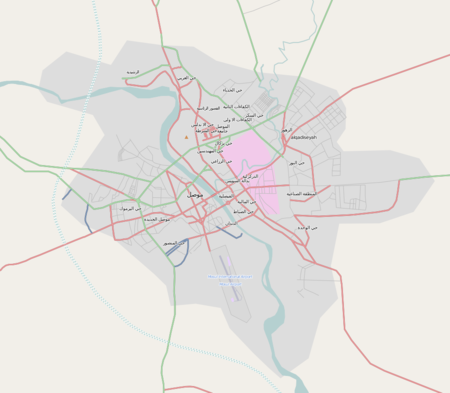
لمعانٍ أخرى، طالع الموصل (توضيح). الموصل مووسڵ، Mûsil ܡܘܨܠ ضفة نهر دجلة في مدينة الموصل الموصلشعار المدينة الموقع الجغرافي اللقب مدينة الحدباء، أم الربيعين، مدينة الرماح تقسيم إداري البلد العراق[1][2] عاصمة لـ محافظة نينوىالدولة الزنكيةولاية الموصل المح...

Malaysian politician This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article is written like a personal reflection, personal essay, or argumentative essay that states a Wikipedia editor's personal feelings or presents an original argument about a topic. Please help improve it by rewriting it in an encyclopedic style. (July 2018) (Learn how and when to remove this message) This articl...

This article is about a shopping centre in Melbourne, Australia. For the railway station, see Melbourne Central railway station. Shopping mall in Victoria, AustraliaMelbourne CentralLocationMelbourne, Victoria, AustraliaCoordinates37°48′37.42″S 144°57′47.32″E / 37.8103944°S 144.9631444°E / -37.8103944; 144.9631444Opening date1991; 33 years ago (1991)[1]DeveloperKumagai GumiManagementGPT GroupOwnerGPT Group[2]ArchitectKisho...

Chemical compound CyclotriolClinical dataOther namesZK-136295; Cycloestriol; 14α,17α-Ethanoestriol; 14α,17α-Ethanoestra-1,3,5(10)-triene-3,16α,17β-triol; 14,21-Cyclo-19-norpregna-1,3,5(10)-triene-3,16α,17α-triolRoutes ofadministrationBy mouth[1]Drug classEstrogenPharmacokinetic dataBioavailability40%[1]Elimination half-life12.3 hours[1]Identifiers IUPAC name (8R,9S,13S,14S,16R,17R)-13-Methyl-7,8,9,11,12,13,15,16-octahydro-14,17-ethanocyclopenta[a]phenanthrene-3...

Location of New York in the United States Gun laws in New York regulate the sale, possession, and use of firearms and ammunition in the U.S. state of New York, outside of New York City which has separate licensing regulations. These regulations are very strict in comparison to the rest of the United States.[1] New York Civil Rights Law art. II, § 4 provides that A well regulated militia being necessary to the security of a free state, the right of the people to keep and bear arms ca...

2010 Spanish Grand Prix Race 5 of 19 in the 2010 Formula One World Championship← Previous raceNext race → Circuit de CatalunyaRace detailsDate 9 May 2010Official name Formula 1 Gran Premio de España Telefónica 2010Location Circuit de Catalunya, Montmeló, Catalonia, Spain[1]Course Permanent racing facilityCourse length 4.655 km (2.892 miles)Distance 66 laps, 307.104 km (190.826 miles)Weather Mainly cloudy, dryAttendance 98,200Pole positionDriver Mark Webber R...

Disambiguazione – Se stai cercando altri significati, vedi Fiat 600 (disambigua). Fiat 600Descrizione generaleCostruttore FIAT Tipo principaleBerlina Produzionedal 1955 al 1969 Sostituita daFiat 850 Esemplari prodotti2 695 197[1] +2 226 000 circa su licenza Altre caratteristicheDimensioni e massaLunghezza3215 mm Larghezza1380 mm Altezza1405 mm Passo2000 mm Massa585 kg AltroAssemblaggioTorino (Fiat Mirafiori)Kragujevac (Jugoslav...

Keyboard layout The BÉPO layout is an optimized French keyboard layout developed by the BÉPO community,[1] supporting all Latin-based alphabets of the European Union, Greek, and Esperanto.[2] It is also designed to ease programming. It is based on ideas from the Dvorak and other ergonomic layouts. Typing with it is usually easier due to the high frequency keys being in the home row. Typing tutors exist to ease the transition.[3] In 2017, the BÉPO layout was the obje...

Gereja di Neftekamsk Eparki Neftekamsk adalah sebuah eparki Gereja Ortodoks Rusia yang terletak di Neftekamsk, Federasi Rusia. Eparki tersebut didirikan pada tahun 2011.[1] Referensi ^ http://www.patriarchia.ru/db/text/1912999.html lbsKeuskupan Gereja Ortodoks RusiaPatriark MoskwaEparki di Rusia Abakan dan Khakassia Akhtubinsk Alapayevsk Alatyr Alexdanrov Almetyevsk Amur Anadyr Ardatov Arkhangelsk Armavir Arsenyev Astrakhan Balashov Barnaul Barysh Belgorod Belyov Bezhetsk Birobidzhan ...












































![{\displaystyle [0,t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37d2d2fa44908c699e2b7b7b9e92befc8283f264)
![{\displaystyle [0,t]\times \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b69365f1419525ab7835544755e6edc98add09c0)
![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)


![{\displaystyle [0,1]\times \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/471cfe49564c93148c0785222437bc7b8efbcdc1)














































![{\displaystyle \xi \mapsto [f(x_{i})/x_{i}]\xi .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a12cab831a883a233a54304b0aabe7c8eb0d3fd7)







