Arakelov theory
|
Read other articles:

Peta lokasi Kabupaten Magetan di Jawa Timur Berikut adalah daftar kecamatan dan kelurahan/desa di Kabupaten Magetan, Provinsi Jawa Timur, Indonesia. Kabupaten Magetan terdiri dari 18 kecamatan, 28 kelurahan, dan 207 desa. Pada tahun 2017, jumlah penduduknya mencapai 687.057 jiwa dengan luas wilayah 688,84 km² dan sebaran penduduk 997 jiwa/km².[1][2] Daftar kecamatan dan kelurahan di Kabupaten Magetan, adalah sebagai berikut: Kode Kemendagri Kecamatan Jumlah Kelurahan Jumlah ...

Radio station in Fuquay-Varina, North CarolinaWNNLFuquay-Varina, North CarolinaBroadcast areaRaleigh/DurhamResearch TriangleFrequency103.9 MHz (HD Radio)BrandingThe Light 103.9ProgrammingFormatUrban GospelSubchannelsHD2: WDRU simulcastOwnershipOwnerUrban One(Radio One Licenses, LLC)Sister stationsWFXC, WFXK, WQOKHistoryFirst air date1981; 43 years ago (1981)Former call signsWAKS-FM (1978–1987)WAZZ (1987–1989)WNND (1989–1996)WTCD (1996)WZZU-FM (1996–1998)[1]Ca...
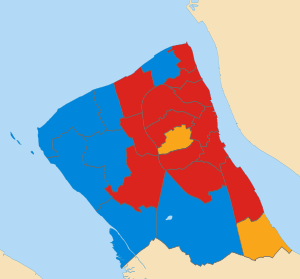
2016 local election in England Main article: 2016 United Kingdom local elections 2016 Wirral Metropolitan Borough Council election ← 2015 5 May 2016 (2016-05-05) 2018 → 23 of 66 seats (One Third and one by-election)to Wirral Metropolitan Borough Council34 seats needed for a majorityTurnout35.6% (33.5%)[1] First party Second party Leader Phil Davies Jeff Green Party Labour Conservative Leader's seat BirkenheadandTranmere West Kirb...

American physician and physiologist This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Dickinson W. Richards – news · newspapers · books · scholar · JSTOR (Au...

ロバート・デ・ニーロRobert De Niro 2011年のデ・ニーロ生年月日 (1943-08-17) 1943年8月17日(80歳)出生地 アメリカ合衆国・ニューヨーク州ニューヨーク市身長 177 cm職業 俳優、映画監督、映画プロデューサージャンル 映画、テレビドラマ活動期間 1963年 -配偶者 ダイアン・アボット(1976年 - 1988年)グレイス・ハイタワー(1997年 - )主な作品 『ミーン・ストリート』(1973年)...

Variety of potato Adirondack RedAdirondack Red potato tuberSpeciesSolanum tuberosumCultivar'Adirondack Red'OriginUnited States, 2003 Adirondack Red is a potato variety with red flesh and skin, bred by Cornell University potato breeders Robert Plaisted, Ken Paddock and Walter De Jong, and released in 2004. The Adirondack varieties are unusual because both the skin and the flesh are colored and have high levels of anti-oxidants.[1] They are described as Early- to mid-season, medium- to ...

CBS affiliate in Toledo, Ohio WTOLToledo, OhioUnited StatesChannelsDigital: 11 (VHF)Virtual: 11BrandingWTOL 11[1]WTOL 11 NewsProgrammingAffiliations11.1: CBSfor others, see § SubchannelsOwnershipOwnerTegna Inc.(WTOL Television, LLC)Sister stationsWUPWHistoryFoundedDecember 5, 1958 (65 years ago) (1958-12-05)Former channel number(s)Analog: 11 (VHF, 1958–2009)Digital: 17 (UHF, 2002–2009)[1]Former affiliationsNBC (secondary, 1958–1969)Call sign meaningTo...

A household hazardous waste collection center in Seattle, Washington, U.S. Under United States environmental policy, hazardous waste is a waste (usually a solid waste) that has the potential to: cause, or significantly contribute to an increase in mortality or an increase in serious irreversible, or incapacitating reversible illness; or pose a substantial present or potential hazard to human health or the environment when improperly treated, stored, transported, or disposed of, or otherwise ...

Louvie-JuzoncomuneLouvie-Juzon – Veduta LocalizzazioneStato Francia Regione Nuova Aquitania Dipartimento Pirenei Atlantici ArrondissementOloron-Sainte-Marie CantoneOloron-Sainte-Marie-2 TerritorioCoordinate43°06′N 0°25′W / 43.1°N 0.416667°W43.1; -0.416667 (Louvie-Juzon)Coordinate: 43°06′N 0°25′W / 43.1°N 0.416667°W43.1; -0.416667 (Louvie-Juzon) Altitudineda 318 a 2 038 m s.l.m. Superficie56,33 km² Abitanti1&#...
كاترين الإسكندرانية معلومات شخصية الميلاد 287الإسكندرية الوفاة 305الإسكندرية سبب الوفاة قطع الرأس مواطنة روما القديمة الحياة العملية المهنة مبشرة تعديل مصدري - تعديل كاترينا الإسكندرانية، لوحة لكارلو كريفيلي كاترينا الإسكندرانية (باليونانية: ἡ Ἁγία Αἰκατε...

King NothingSingel oleh Metallicadari album LoadSisi-BAin't My Bitch (live)Dirilis7 January 1997[1]FormatCD singlecassetteDirekamMei 1995 – Februari 1996 di The Plant Studios, in Sausalito, CaliforniaGenreHeavy metalDurasi5:28LabelElektraPenciptaJames HetfieldLars UlrichKirk HammettProduserBob RockJames HetfieldLars UlrichKronologi singel Metallica Mama Said (1996) King Nothing (1997) The Memory Remains (1997) Video musikKing Nothing di YouTube King Nothing merupakan salah satu sing...

Royal Navy Admiral (1856–1917) Sir Frederick Hamilton1917 portrait by Francis DoddBorn(1856-03-08)8 March 1856London, EnglandDied4 October 1917(1917-10-04) (aged 61)Rosyth, ScotlandAllegiance United KingdomService/branch Royal NavyYears of service1869–1917RankAdmiralCommands heldHMS Rattlesnake[1]HMS Bulwark[2]Commander-in-Chief, RosythBattles/warsZulu WarFirst World WarAwardsKnight Grand Cross of the Royal Victorian OrderKnight Commander of t...

Since 2023 These are tables of congressional delegations from South Carolina to the United States House of Representatives and the United States Senate. The current dean of the South Carolina delegation is Representative Jim Clyburn (SC-6), having served in the House since 1993. U.S. House of Representatives Main article: List of United States representatives from South Carolina Current members The current U.S. House delegation from South Carolina has 7 members, including 6 Republicans and 1...

Complex exponential in terms of sine and cosine This article is about Euler's formula in complex analysis. For other uses, see List of things named after Leonhard Euler § Formulae. Part of a series of articles on themathematical constant e Properties Natural logarithm Exponential function Applications compound interest Euler's identity Euler's formula half-lives exponential growth and decay Defining e proof that e is irrational representations of e Lindemann–Weierstrass theorem People...

Scientology term Part of a series onScientology General Scientology Dianetics Timeline History L. Ron Hubbard Publications Glossary Beliefs and practices Thetan Auditing Bridge to Total Freedom OT Xenu Ethics and justice Church of Scientology Officials and staff Sea Org David Miscavige Controversies Litigation Status by country Suppressive person Disconnection Fair game RPF The Hole Office of Special Affairs Guardian's Office War on psychiatry More MEST is an acronym for matter, energy, space...

Football team 1944 Pittsburgh Panthers footballConferenceIndependentRecord4–5Head coachClark Shaughnessy (2nd season)Home stadiumPitt StadiumSeasons← 19431945 → 1944 Eastern college football independents records vte Conf Overall Team W L T W L T No. 1 Army – 9 – 0 – 0 Yale – 7 – 0 – 1 Harvard – 5 – 1 – 0 Bucknell – 7 ...

Questa voce sull'argomento chimici britannici è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. J. Mercer John Mercer (Great Harwood, Lancashire, 21 febbraio 1791 – 30 novembre 1866) è stato un chimico e industriale tessile britannico, fu uno studioso delle fibre tessili e delle sostanze coloranti. Viene ricordato soprattutto per la messa a punto nel 1844 del trattamento della cellulosa con soda caustica (detto mercerizzazione) che brevettò nel 1851...

Village in Guam, United StatesYigo, GuamVillageRitidian Point, the northernmost point on Guam, in the Guam National Wildlife RefugeLocation of Yigo within the Territory of Guam.CountryUnited StatesTerritoryGuamGovernment • MayorAnthony Tony P. Sanchez (R) • Vice MayorLoreto V. Leones (R)Area • Total35 sq mi (90 km2)Elevation587 ft (179 m)Population (2020)[1] • Total19,339Time zoneUTC+10 (ChST) Yigo, Guam (Ch...

Someone with an affinity for Swedish culture and language A Dalecarlian horse, a traditional symbol for Swedish folk culture, in Cloquet, Minnesota A Suecophile (or Swedophile)[1][2] is someone, typically a non-Swede, with a great interest in the culture and language of Sweden.[3][4] In the language debate in Finland in the 19th and 20th centuries, the Svecoman movement was formed by those who preferred the Swedish language to the Finnish language. The word Sue...

Voce principale: Delfino Pescara 1936. Delfino Pescara 1936Stagione 2014-2015Sport calcio Squadra Pescara Allenatore Marco Baroni[1], poi Massimo Oddo All. in seconda Primo Maragliulo,[1] poi, Marcello Donatelli Presidente Daniele Sebastiani Serie B7° (qualificato ai play-off) Coppa ItaliaQuarto Turno Miglior marcatoreCampionato: Melchiorri (14)Totale: Melchiorri (14) StadioAdriatico (20,515) Abbonati3 545[2] Maggior numero di spettatori10 689 vs Bari (20 marzo ...


























![{\displaystyle {\hat {\mathrm {ch} }}(f_{*}([E]))=f_{*}({\hat {\mathrm {ch} }}(E){\widehat {\mathrm {Td} }}^{R}(T_{X/Y}))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4983345b315a5a94624d3f4ebb931e5501d47b7)




![{\displaystyle \sum _{m>0 \atop m{\text{ odd}}}{\frac {X^{m}}{m!}}\left[2\zeta '(-m)+\zeta (-m)\left({1 \over 1}+{1 \over 2}+\cdots +{1 \over m}\right)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39aa3cc34a6059301aa48b002f77778a487f9ef5)