Albanese variety
|
Read other articles:

FC Viktoria KölnNama lengkapFußballclub Viktoria Köln 1904 e. V.Berdiri22 Juni 2010StadionSportpark Höhenberg(Kapasitas: 8,317)ManajerStephan KüstersPelatihOlaf JanßenLiga3. Fußball-Liga (III)2022–239th Kostum kandang Kostum tandang FC Viktoria Köln adalah tim sepak bola amatir asal Jerman yang berdomisili di Cologne, North Rhine-Westphalia. Skuat terkini Hingga 7 Juli 2013[update] Catatan: Bendera menunjukkan tim nasional sesuai dengan peraturan FIFA. Pemain dapat...

العلاقات المالديفية الموريشيوسية جزر المالديف موريشيوس المالديف موريشيوس تعديل مصدري - تعديل العلاقات المالديفية الموريشيوسية هي العلاقات الثنائية التي تجمع بين المالديف وموريشيوس.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرج�...

العلاقات الإكوادورية الميانمارية الإكوادور ميانمار الإكوادور ميانمار تعديل مصدري - تعديل العلاقات الإكوادورية الميانمارية هي العلاقات الثنائية التي تجمع بين الإكوادور وميانمار.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية �...

A soil scientist is a contributor to soil science. Soil scientists include agrologists, pedologists and soil classifiers. The following is a list of notable soil scientists. Name Birth/death Country Remark William Albrecht 1888–1974 USA Joselito (Lito) M. Arocena 1959–2015 Canada Founding member of University of Northern British Columbia and became its first Canada Research Chair in 2001 Mary C. Baltz 1923–2011 USA First woman soil scientist officially assigned in the field for NRCS Ve...

Cet article est une ébauche concernant un coureur cycliste lituanien et un coureur cycliste soviétique. Vous pouvez partager vos connaissances en l’améliorant (comment ?). Pour plus d’informations, voyez le projet cyclisme. Gintautas UmarasInformationsNom court Гинтаутас УмарасNaissance 20 mai 1963 (60 ans)KaunasNationalité lituanienneDistinction Maître émérite du sport de l'URSSÉquipes professionnelles 1989Alfa Lum1990-1991Coors LightPrincipales victoire...

Dawei ထားဝယ်TavoyKotaKoordinat: 14°05′0″N 98°12′0″E / 14.08333°N 98.20000°E / 14.08333; 98.20000Negara MyanmarRegionRegion TanintharyiDistrikDistrik DaweiIbukotaDaweiPopulasi (2014)146.964 • AgamaBuddha TheravadaZona waktuUTC+6.30 (MMT)Kode area telepon+95 59[1] Dawei (Burma: ထားဝယ်code: my is deprecated ) adalah sebuah kota di Myanmar tenggara dan merupakan ibukota Region Tanintharyi, yang sebelumnya di...

American politician Thomas WalshMember of theMassachusetts House of Representativesfrom the 12th Essex districtIncumbentAssumed office 2016Preceded byLeah Cole AllenIn office1987–1995Preceded byTheodore C. SpeliotisSucceeded byJohn P. Slattery Personal detailsBorn (1960-07-15) July 15, 1960 (age 63)Salem, MassachusettsPolitical partyDemocraticResidencePeabody, MassachusettsAlma materSalem State University (formerly Salem State College)OccupationAccount ManagerPolitician Thomas P. W...

American cornetist and jazz pioneer (1877–1931) Charles Buddy BoldenBolden c. 1905Background informationBirth nameCharles Joseph BoldenBorn(1877-09-06)September 6, 1877New Orleans, Louisiana, U.S.DiedNovember 4, 1931(1931-11-04) (aged 54)Jackson, Louisiana, U.S.GenresJazzbluesOccupation(s)MusicianInstrument(s)CornetYears active1890s–1907Musical artist Charles Joseph Buddy Bolden (September 6, 1877 – November 4, 1931) was an American cornetist who was regarded by contempor...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要編修,以確保文法、用詞、语气、格式、標點等使用恰当。 (2013年8月6日)請按照校對指引,幫助编辑這個條目。(幫助、討論) 此條目剧情、虛構用語或人物介紹过长过细,需清理无关故事主轴的细节、用語和角色介紹。 (2020年10月6日)劇情、用語和人物介紹都只是用於了解故事主軸,輔助�...

Extinct family of mammals GroeberiidaeTemporal range: Eocene - Oligocene 45–28 Ma PreꞒ Ꞓ O S D C P T J K Pg N Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Mammalia Clade: Theriiformes Family: †GroeberiidaePatterson, 1952 Genera †Epiklohnia? †Groeberia †Klohnia? †Praedens? Synonyms Groeberidae Groeberiidae is a family of strange non-placental mammals from the Eocene and Oligocene epochs of Patagonia, Argentina and Chile, South Ameri...

الأشعث بن قيس تخطيط الاسم الأشعث بن قيس. معلومات شخصية اسم الولادة معديكرب بن قيس الميلاد 23 ق هـ/ 599 مشبوة الوفاة 40 هـ/ 661 مالكوفة مواطنة الخلافة الراشدة الكنية أبو محمد اللقب الأشعث الديانة الإسلام الأولاد جعدة بنت الأشعثمحمد بن الأشعث إخوة وأخوات سيف بن قيس[1]إبر...
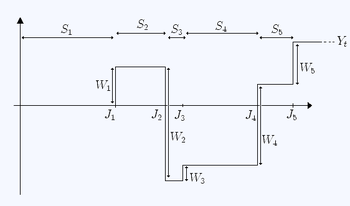
Branch of probability theory Renewal theory is the branch of probability theory that generalizes the Poisson process for arbitrary holding times. Instead of exponentially distributed holding times, a renewal process may have any independent and identically distributed (IID) holding times that have finite mean. A renewal-reward process additionally has a random sequence of rewards incurred at each holding time, which are IID but need not be independent of the holding times. A renewal process h...

International non-governmental organization Not to be confused with International Code of Zoological Nomenclature. International Commission on Zoological NomenclatureAbbreviationICZNFormation18 September 1895; 128 years ago (1895-09-18)TypeInternational non-governmental organizationLocationNational University of Singapore, SingaporeRegion served WorldwideOfficial language English, FrenchMain organBulletin of Zoological NomenclatureAffiliationsInternational Union of Biologica...
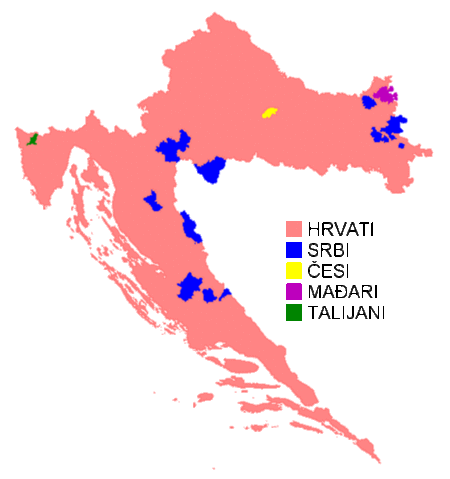
This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Czechs of Croatia – news · newspapers · books · scholar · JSTOR (August 2010) (Learn how and when to remove this message) Ethnic group Czechs of CroatiaČesi u HrvatskojČeši v ChorvatskuCoat of arms of the Czechs in CroatiaTotal population9,641 (2011)[1&#...

Czech tennis player career statistics Career finals Discipline Type Won Lost Total WR Singles Grand Slam – – – – Summer Olympics – – – – WTA Finals – – – – WTA 1000[a] – – – – WTA 500[b] & 250[c] 5 5 10 0.50 Total 5 5 10 0.50 Doubles Grand Slam 8 2 10 0.80 Summer Olympics 1 0 1 1.00 WTA Finals 1 2 3 0.33 WTA 1000[a] 4 4 8 0.50 WTA 500[b] & 250[c] 11 9 20 0.55 Total 25 17 42 0.59 Total 30 22 52 0.58 Siniako...

American actor and comedian (1944–2023) Richard BelzerBelzer at the White House Correspondents Dinner in 2009BornRichard Jay Belzer(1944-08-04)August 4, 1944Bridgeport, Connecticut, U.S.DiedFebruary 19, 2023(2023-02-19) (aged 78)Bozouls, France[1]EducationFairfield Warde High SchoolDean CollegeOccupationsActorcomedianauthorSpouses Gail Susan Ross (m. 1966; div. 1972) Dalia Danoch (m. 1976; d...

Human hormone This article is about dihydrotestosterone as a hormone. For its use as a medication, see Androstanolone. This article is about 5α-dihydrotestosterone, an androgen. For the inactive 5β isomer, see 5β-Dihydrotestosterone. Dihydrotestosterone Names IUPAC name 17β-Hydroxy-5α-androstan-3-one Systematic IUPAC name (1S,3aS,3bR,5aS,9aS,9bS,11aS)-1-Hydroxy-9a,11a-dimethylhexadecahydro-7H-cyclopenta[a]phenanthren-7-one Other names DHT; 5α-Dihydrotestosterone; 5α-DHT; Androstanolone...

尼泊尔联邦民主共和国副总统 (尼泊爾語:नेपालका उपराष्ट्रपतिहरू, Nēpālakā uparāṣṭrapatiharū)是尼泊尔的国家副元首,於2008年5月废除尼泊尔君主制时设立。副总统的正式稱謂为“阁下”。[1]现任尼泊尔副总统是拉姆·萨哈亚·亚达夫(英语:Ram Sahaya Yadav)。 尼泊尔联邦民主共和国副总统尼泊尔国徽現任拉姆·萨哈亚·亚达夫(英语:Ram Sa...

Shipyard in San Diego, CA, USA National Steel and Shipbuilding CompanyCompany typeSubsidiaryIndustryShipbuildingFounded1905; 119 years ago (1905)HeadquartersSan Diego, California, USNumber of locationsSan Diego, California; Norfolk, Virginia; Mayport, Florida; Bremerton, WashingtonKey peopleDavid Carver[1] (President)ParentGeneral DynamicsSubsidiariesTIMSAWebsitewww.nassco.com The amphibious assault ship USS Bonhomme Richard (LHD-6) in dry dock at NASSCO shipyard in ...

Armenian Catholic cathedral in Gyumri, Armenian Cathedral of the Holy MartyrsCathedral of the Holy MartyrsReligionAffiliationArmenian Catholic ChurchYear consecrated24 September 2015LocationLocationVictory (Haghtanak) Avenue, Gyumri, Shirak Province, ArmeniaArchitectureArchitect(s)Hakob JivanyanTypeArmenianStyleCircular styleGroundbreaking8 December 2010Completed2015Dome(s)1 Cathedral of the Holy Martyrs (Armenian: Սրբոց Նահատակաց եկեղեցի), in Gyumri, Armenia, is the cath...












