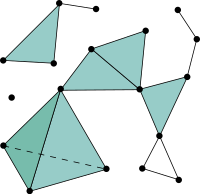
Abstract simplicial complex
|
Read other articles:

Group of stereoisomers AminoglutethimideClinical dataTrade namesElipten, Cytadren, Orimeten, numerous othersOther namesAG; AGI; Ba 16038; Ciba 16038; ND-1966; 2-(p-Aminophenyl)-2-ethylglutarimideAHFS/Drugs.comConsumer Drug InformationMedlinePlusa604039Pregnancycategory AU: D Routes ofadministrationBy mouthDrug classAromatase inhibitor; Antiestrogen; Steroidogenesis inhibitor; AntiglucocorticoidATC codeL02BG01 (WHO) Pharmacokinetic dataBioavailabilityRapid, complete[1]Me...

Kesalahan pengutipan: Tag <ref> tidak sah; referensi tanpa nama harus memiliki isiArtikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Gua Maria Sendang Klayu – berita · surat kabar · buku · cendekiawan · JSTOR artikel ini perlu dirapikan agar memenu...

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

Перуанский анчоус Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеГруппа:Костные рыбыКласс:Лучепёрые рыбыПодкласс:Новопёрые �...

Pour les articles homonymes, voir GCD. Cet article est une ébauche concernant les comics. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Logo du Grand Comics Database. La Grand Comics Database (GCD ; en français : « Grande base de données de la bande dessinée ») est une base de données en ligne visant à répertorier l'ensemble des bandes dessinées publiées dans le monde sous divers...

Questa voce sull'argomento film drammatici è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Al di là della vitaTom Sizemore e Nicolas Cage in una scena del filmTitolo originaleBringing Out the Dead Lingua originaleinglese, spagnolo Paese di produzioneStati Uniti d'America Anno1999 Durata121 min Rapporto2,35:1 Generedrammatico RegiaMartin Scorsese SoggettoJoe Connelly (dal romanzo Bringing Out the Dead) SceneggiaturaPaul Schrader ProduttoreBarbara De F...

Chinese politician, activist, and linguist In this Chinese name, the family name is Ma. Ma Xulun as a professor at Peking University. Ma Xulun (simplified Chinese: 马叙伦; traditional Chinese: 馬敘倫; Wade–Giles: Ma Hsü-lun, 27 April 1885 – 4 May 1970), courtesy name Yichu (Chinese: 彝初), was a Chinese politician, activist, and linguist. He was one of the co-founders of the China Association for Promoting Democracy. Early life Ma Xulun was an early m...

尊敬的拿督斯里莫哈末·沙布Mohamad bin Sabu国会议员2018年9月24日末沙布在五角大楼与美国国防部长詹姆斯·马蒂斯会面农业及食品工业部部长现任就任日期2022年12月3日君主最高元首苏丹阿都拉最高元首苏丹依布拉欣·依斯迈首相安华·依布拉欣副职陈泓缣(2022年至2023年)亚瑟古律(2023年至今)前任羅納建迪国防部长任期2018年5月21日—2020年2月24日君主最高元首端姑莫哈末五世...

2015 filmRememberTheatrical release posterDirected byAtom EgoyanWritten byBenjamin AugustProduced by Robert Lantos Ari Lantos Starring Christopher Plummer Bruno Ganz Jürgen Prochnow Heinz Lieven Henry Czerny Dean Norris Martin Landau CinematographyPaul SarossyEdited byChristopher DonaldsonMusic byMychael DannaProductioncompanies Egoli Tossell Film Serendipity Point Films Distributed by Entertainment One (Canada) Tiberius Film (Germany) IM Global (International)[1] Release dates Sept...

English rock singer; frontman of the Rolling Stones (born 1943) SirMick JaggerJagger in 2022BornMichael Philip Jagger (1943-07-26) 26 July 1943 (age 80)Dartford, Kent, EnglandOccupations Singer songwriter musician actor film producer dancer Years active1960–presentSpouse Bianca Pérez-Mora Macias (m. 1971; div. 1978)PartnersJerry Hall (1977–1999)L'Wren Scott (2001–2014; her death)Melanie Hamrick (2014–present)Children8...

Marvel Studios film Black WidowTheatrical release posterDirected byCate ShortlandScreenplay byEric PearsonStory by Jac Schaeffer Ned Benson Based onMarvel ComicsProduced byKevin FeigeStarring Scarlett Johansson Florence Pugh David Harbour O-T Fagbenle Olga Kurylenko William Hurt Ray Winstone Rachel Weisz CinematographyGabriel BeristainEdited by Leigh Folsom Boyd Matthew Schmidt Music byLorne BalfeProductioncompanyMarvel StudiosDistributed byWalt Disney StudiosMotion PicturesRelease dates June...

Earth blocks for construction New, unlaid mudbricks in the Jordan Valley, West Bank Palestine, (2011) Mudbrick was used for the construction of Elamite ziggurats—some of the world's largest and oldest constructions. Choqa Zanbil, a 13th-century BCE ziggurat in Iran, is similarly constructed from clay bricks combined with burnt bricks.[1] Mudbrick or mud-brick, also known as unfired brick, is an air-dried brick, made of a mixture of mud (containing loam, clay, sand and water) mixed w...

French attack/interceptor aircraft Mirage 5 Chilean Air Force Mirage 5MA Role Attack aircraft Fighter-bomberType of aircraft National origin France Manufacturer Dassault Aviation First flight 19 May 1967 Status Active Primary users French Air Force (historical)Belgian Air Force (historical) Egyptian Air Force Pakistan Air Force Number built 582 Developed from Dassault Mirage III Variants IAI Nesher Developed into IAI Kfir The Dassault Mirage 5 is a French supersonic attack aircraft/fight...

Percussion instrument This article is about the instrument. For other uses, see Bell (disambiguation). For technical reasons, Bell #9801 redirects here. For the memorial with that title, see Bell 9801. BellParts of a typical tower bell hung for swinging: 1. Bell yoke or headstock, 2. canons, 3. crown, 4. shoulder, 5. waist, 6. sound bow, 7. lip, 8. mouth, 9. clapper, 10. bead linePercussion instrumentClassification Struck idiophoneHornbostel–Sachs classification111.242(Bells: Percussion ves...

För andra betydelser, se 1830 (olika betydelser). 1830 – MDCCCXXX194 år sedan År1827 | 1828 | 182918301831 | 1832 | 1833 Årtionde1810-talet | 1820-talet 1830-talet1840-talet | 1850-talet Århundrade1700-talet 1800-talet1900-talet Årtusende1000-talet Året Födda | AvlidnaBildanden | Upplösningar Humaniora och kulturKonst, litteratur, musik och teater Samhällsvetenskapoch samhälleKrig | Sport Teknik ...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (يوليو 2019) منتخب التشيك لدوري الرغبي تعديل مصدري - تعديل منتخب التشيك الوطني لدوري الر...

Regional language of France This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Champenois language – news · newspapers · books · scholar · JSTOR (January 2021) (Learn how and when to remove this message) ChampenoischampaignatNative toFrance, BelgiumRegionChampagne-Ardenne, Île-de-France (Seine-et-Marne), ...

Michael LerjéusInformazioni personaliArbitro di Calcio Federazione Svezia ProfessioneUfficiale militare Attività nazionale AnniCampionatoRuolo 2002-2014 2006-2015Superettan AllsvenskanArbitro Arbitro Attività internazionale AnniConfederazioneRuolo 2009-2015UEFA e FIFAArbitro Jan Michael Lerjéus (Skövde, 18 giugno 1973) è un ex arbitro di calcio svedese. Indice 1 Carriera 2 Note 3 Altri progetti 4 Collegamenti esterni Carriera Lerjéus è un arbitro affiliato alla Federcalcio svedes...

Elected administrative body governing an area known as a county A county council is the elected administrative body governing an area known as a county. This term has slightly different meanings in different countries. Norway In Norway, a county council (Norwegian: Fylkesting) is the highest governing body of a county municipality (fylkeskommune). The county council sets the scope of the county municipal activity. The council is led by the Chairman of the County Council, more commonly called ...

Cet article est une ébauche concernant une localité italienne et la Lombardie. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Marcaria Administration Pays Italie Région Lombardie Province Mantoue Code postal 46010 Code ISTAT 020031 Code cadastral E922 Préfixe tel. 0376 Démographie Population 6 358 hab. (31-05-2022[1]) Densité 71 hab./km2 Géographie Coordonnées 45° 07′&...









![{\displaystyle [0,1]^{S}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f034b8ba7ce60e422fe66ec6ec411277793d55e4)
![{\displaystyle t\colon S\to [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8c72ad64f610a407bac29048577141ae0171bd5)


![{\displaystyle [0,1]^{A}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f56f4c21500c8a6384207a1e492aebc34d9ec6d1)



![{\displaystyle S=K[x_{1},\dots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cafcb2abee81375c819a9b39da5621729975778f)

![{\displaystyle \mathbf {a} \in \{0,1\}^{n}\mapsto \{i\in [n]:a_{i}=1\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26112483a09c7764f992cfd056afa64b1d771e82)



