1948 in American television

List of years in American television:
1947–48 United States network television schedule
1948–49 United States network television schedule
List of American television programs currently in production

This is a list of American television-related events in 1948.

Events

Date Event Ref.
March 4 The C. E. Hooper Company releases the first-ever American television ratings. [1][page needed]
April 3 The NBC Symphony Orchestra, conducted by Robert Shaw, is first telecast. In this broadcast, Beethoven's Symphony No. 9 is played in its entirety for the first time on television, and in concert.
April 18 The American Broadcasting Company begins operations as a television network, with its New York City-based station WJZ-TV serving as network flagship. [2][page needed]
May 3 CBS Television News premieres as the first network nightly newscast, hosted by journalist Douglas Edwards.
June 21 The 1948 Republican National Convention in Philadelphia, Pennsylvania becomes the first political convention to be telecast by the networks.
July 30 The DuMont Television Network becomes the first network to televise professional wrestling in prime time.
November Screen Gems was founded as the television subsidiary of Columbia Pictures Corporation.
November 25 CBS broadcasts its earliest known national telecast of the Macy's Thanksgiving Day Parade.
November 29 CBS telecasts the first broadcast of a roller derby match.
Unknown date Ziv Television Programs was created by Frederick Ziv as a subsidiary of the Ziv Company, in order to specialize in the production of original television programs for syndication [3]

Other television events in 1948

  • CBS begins television network programming.
  • The number of homes in the United States with a television set reaches one million.

Television programs

Debuts

Date Debut Network
January Camera Headlines DuMont
January I.N.S. Telenews
January 9 Playroom
January 18 The Original Amateur Hour
February 9 Court of Current Issues
March 4 Stop Me If You've Heard This One NBC
March 9 The Johns Hopkins Science Review CBS
April 4 Author Meets the Critics NBC
April 14 Scoreboard DuMont
April 15 For Your Pleasure[4] NBC
Hollywood Screen Test ABC
May 21 What's It Worth CBS
June 1 We the People CBS
June 8[5] Texaco Star Theater NBC
June 20[6] The Ed Sullivan Show CBS
July 4 Key to the Missing DuMont
August 10 Candid Camera ABC
August 11 Quizzing the News ABC
August 11 The Laytons DuMont
August 12 Club Seven ABC
August 15 CBS Television News CBS
August 16 Places Please CBS
August 23 Foodini the Great CBS
August 27 Teenage Book Club ABC
September 6 Champagne and Orchids DuMont
September 21 Operation Success DuMont
September 26[7] Actors Studio ABC
Stained Glass Windows unknown
September 27[8] The Chevrolet Tele-Theatre NBC
October 3[9] The Philco Television Playhouse NBC
October 17 The Ford Television Theatre CBS
October 19 Off the Record DuMont
October 20 The Growing Paynes DuMont
October 22 Break the Bank ABC
October 29 Tales of the Red Caboose DuMont
November 1[10] Okay, Mother WABD
Your Television Babysitter Dumont
TV Shopper
Amanda
November 4 The Adventures of Oky Doky
Fashions on Parade
November 7 Newsweek Views the News DuMont
Studio One CBS
November 20 Celebrity Time CBS
November 21 Lamp Unto My Feet CBS
December 6 Arthur Godfrey's Talent Scouts CBS
December 17 The Morey Amsterdam Show CBS
Unknown date The Alan Dale Show Dumont
The Philco Television Playhouse NBC
The Stan Shaw Show Dumont
Your School Reporter
Wrestling From Columbia Park Arena
Wrestling From Jamaica Arena
The Needle Shop

Changes of network affiliation

Show Moved from Moved to
Author Meets the Critics NBC ABC
Mary Kay and Johnny DuMont NBC

Ending this year

Date Show Network Debut Notes
January The Walter Compton News DuMont June 16, 1947
May 9 Playroom DuMont January 9, 1948
June 30 In the Kelvinator Kitchen NBC May 21, 1947
October 29 Teenage Book Club ABC August 27, 1948
Unknown date The World in Your Home NBC December 22, 1944

Networks and services

Network launches

Network Type Launch date Source
American Broadcasting Company Over-the-air broadcast April 18 [11]
CBS May

Television stations

Station launches

Date City of License/Market Station Channel Affiliation Notes/Ref.
February 9 Cincinnati, Ohio WLWT 5 NBC (primary)
CBS/ABC/DuMont (secondary) 		Successor to experimental station W8XCT.[12]
March 11 Baltimore, Maryland WBAL-TV 11 NBC
April 5 Chicago, Illinois WGN-TV 9 Independent (primary)
CBS/DuMont (secondary)
April 19 Salt Lake City, Utah KDYL-TV 4 NBC
April 22 Richmond, Virginia WTVR-TV 6 NBC (primary)
ABC/DuMont (secondary) 		[13]
April 27 Minneapolis, Minnesota KSTP-TV 5 NBC (primary)
DuMont (secondary)
May 6 Los Angeles, California KTSL 2 DuMont Now KCBS-TV, a CBS O&O station
May 14 Buffalo, New York WBEN-TV 4 NBC (primary)
ABC/DuMont (secondary) 		Now a CBS affiliate since 1949
May 15 Newark, New Jersey
(New York City, New York) 		WATV 13 Independent
May 23 Philadelphia, Pennsylvania WCAU 10 CBS
June 9 Boston, Massachusetts WBZ-TV 4 NBC (primary)
ABC/DuMont (secondary) 		[14]
June 15 New Haven/Hartford, Connecticut WTNH 6
(now 8) 		DuMont (primary)
ABC (secondary)
New York City WPIX 11 Independent
June 21 Boston, Massachusetts WNAC-TV 7 CBS (primary)
ABC/DuMont (secondary) 		Defunct May 22, 1982
July 21 Toledo, Ohio WSPD-TV 13 NBC
August 10 New York City WJZ-TV 7 ABC (O&O)
August 25 Los Angeles, California KFI-TV 9 Independent
September 16 Los Angeles, California KECA-TV 7 ABC (O&O)
September 17 Chicago, Illinois WENR-TV 7 ABC ((O&O)
Los Angeles, California KMTR-TV 13 Independent
September 29 Atlanta, Georgia WSB-TV 8 (now on 2) NBC [15]
Fort Worth/Dallas, Texas WBAP-TV 5 NBC (primary)
ABC (secondary)
October 8 Chicago, Illinois WNBQ 5 NBC
October 9 Detroit, Michigan WXYZ-TV 7 ABC (O&O)
October 24 Detroit, Michigan WJBK 2 CBS (primary)
DuMont (Secondary)
October 31 Cleveland, Ohio WNBK 3 NBC
November 1 Baltimore, Maryland WAAM 13 ABC
November 24 Louisville, Kentucky WAVE-TV 5
(now 3) 		NBC (primary)
CBS/ABC/DuMont (secondary)
November 25 Seattle, Washington KRSC-TV 5 CBS (primary)
DuMont (secondary)
November 29 Albuquerque, New Mexico KOB-TV 4 NBC (primary)
ABC/CBS/DuMont (secondary)
December 1 Syracuse, New York WHEN-TV 5 CBS (primary)
NBC/DuMont (secondary)
December 11 Memphis, Tennessee WMCT 4
(now 5) 		NBC (primary)
ABC/CBS/DuMont (secondary)
December 18 New Orleans, Louisiana WDSU-TV 6 NBC (primary)
DuMont/CBS/ABC (secondary)
December 22 San Francisco, California KPIX-TV 5 CBS (primary)
NBC/DuMont/Paramount (secondary)

Network affiliation changes

Date City of license/Market Station Channel Old affiliation New affiliation Notes/Ref.
October New Haven/Hartford, Connecticut WNHC-TV 6
(now 8) 		DuMont CBS Retains DuMont affiliation on secondary basis until 1956

Births

Main article: 1948 in television § Births

Deaths

Main article: 1948 in television § Deaths

References

  1. ^ "TV 'Amateur Hour' Gets 46.8 Rating". Broadcasting. 1948-03-08. p. 42.
  2. ^ "ABC TV Network". Broadcasting. 1948-04-19.
  3. ^ Newcomb, Horsce (2014). "Ziv Television Programs, Inc.". Encyclopedia of Television. Routledge. pp. 2626–2627. ISBN 9781135194796. Retrieved September 18, 2022.
  4. ^ Hyatt, Wesley (2015). Short Lived Television Series, 1948-1978: Thirty Years of More Than 1,000 Flops. McFarland. p. 5. ISBN 9781476605159. Retrieved September 19, 2022.
  5. ^ "Pop Chronicles 1940s Program #13".
  6. ^ "Ed Sullivan Biography | Ed Sullivan Show". Edsullivan.com. Retrieved 2016-10-28.
  7. ^ Terrace, Vincent (2009). Encyclopedia of Television Shows, 1925 through 2007 (Volume 1). Jefferson, North Carolina: McFarland & Company, Inc. ISBN 978-0-7864-3305-6.
  8. ^ Earle Marsh, Tim Brooks (1979). "The Complete Directory to Prime Time Network TV Shows, 1946-present". Ballantine Books. p. 145. ISBN 0-345-45542-8.
  9. ^ Hawes, William (2001). Live Television Drama, 1946-1951. McFarland. p. 245. ISBN 9781476608495. Retrieved 8 October 2016.
  10. ^ Hyatt, Wesley (1997). The Encyclopedia of Daytime Television. Watson-Guptill Publications. p. 320. ISBN 978-0823083152. Retrieved 22 March 2020.
  11. ^ "ABC TV Network" (PDF). Broadcasting. April 19, 1948. Retrieved September 19, 2022.
  12. ^ "Cincinnati's T-Day Observed Feb. 15". Broadcasting. 1948-02-23.
  13. ^ "WTVR (TV) to Start April 22, Channel 6". Broadcasting. April 19, 1948. Retrieved July 25, 2019.
  14. ^ "WBZ-TV Formally Opened at Boston". Broadcasting. June 14, 1948. Retrieved July 25, 2019.
  15. ^ "WSB-TV in Atlanta Opening on Sept. 29". Broadcasting. September 27, 1948. Retrieved July 27, 2019.

Read other articles:

Giovanna di Trastámara (1455-1517)

Giovanna d'AragonaRegina consorte di NapoliStemma In carica14 settembre 1477 –25 gennaio 1494 PredecessoreIsabella di Chiaromonte SuccessoreGiovanna d’Aragona NascitaBarcellona, 16 giugno 1455 MorteNapoli, 9 gennaio 1517 Casa realeTrastámara d'Aragona PadreGiovanni II d'Aragona MadreGiovanna Enríquez Consorte diFerdinando I di Napoli FigliGiovannella (naturale)Beatrice d'Este (adottiva) ReligioneCattolicesimo Re d'AragonaCasa di Trastámara Ferdinando I Figli Alfonso Maria Gi...

 

 

Criminal Case (permainan)

'Criminal Case' PublikasiFacebook15 November 2012iOS28 Agustus 2014Android15 April 2015GenrePuzzleKarakteristik teknisSistem operasiAndroid dan iOS PlatformAndroid dan iOS ModePermainan video pemain tunggal Formatdistribusi digital dan unduhan digital Metode inputlayar sentuh Format kode Daftar 30 Informasi pengembangPengembangPretty SimplePenerbitGoogle Play dan App Store Penilaian USK Informasi tambahanSitus webcriminalcase.com (Inggris) MobyGamescriminal-case Portal permainan videoSun...

 

 

Slalu, Untuk Sahabat...

Slalu, Untuk Sahabat...Video karya PeterpanDirilis4 november 2006Direkam2003 (2003) – 2005 (2005)GenreRock alternatifPop rockPost-grungeDurasi 41:18 (VCD 1) 35:55 (VCD 2) Label Musica Studio's XL Axiata ProduserCapung, Noey, IcomKronologi Peterpan Alexandria(2005)Alexandria2005 Slalu, Untuk Sahabat...(2006) Hari yang Cerah...(2007)Hari yang Cerah...2007 Slalu, Untuk Sahabat... merupakan album video kedua Peterpan yang dirilis pada tahun 2006 oleh Musica Studio's d...

Peter Linebaugh

American Marxist historian Historian Peter Linebaugh Peter Linebaugh is an American Marxist historian who specializes in British history, Irish history, labor history, and the history of the colonial Atlantic. He is a member of the Midnight Notes Collective. Early life Peter Linebaugh was born in 1942[1] He was a student of British labor historian E. P. Thompson, and received his Ph.D. in British history from the University of Warwick in 1975.[2] He has taught at University of...

 

 

Groupement d'achat service épicerie

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Certaines informations figurant dans cet article ou cette section devraient être mieux reliées aux sources mentionnées dans les sections « Bibliographie », « Sources » ou « Liens externes » (février 2022). Vous pouvez améliorer la vérifiabilité en associant ces informations à des références à l'aide d'appels de notes. Grains de riz Un Groupement d'Achat Service Épic...

 

 

Brett Favre

American football player (born 1969) American football player Brett FavreFavre at Super Bowl 50 in 2016No. 4Position:QuarterbackPersonal informationBorn: (1969-10-10) October 10, 1969 (age 54)Gulfport, Mississippi, U.S.Height:6 ft 2 in (1.88 m)Weight:222 lb (101 kg)Career informationHigh school:Hancock North Central(Kiln, Mississippi)College:Southern Miss (1987–1990)NFL draft:1991 / Round: 2 / Pick: 33Career history As a player: Atlanta Falc...

جامع ملا حسين بسكندي

جامع ملا حسين بسكندي معلومات عامة القرية أو المدينة السليمانية الدولة العراق تاريخ بدء البناء 1317هـ/1899م المواصفات المساحة 2500م2 عدد القباب 1 التفاصيل التقنية المواد المستخدمة الحجر والطابوق النمط المعماري إسلامية تعديل مصدري - تعديل   جامع ملا حسين بسكندي وهو من مساجد ال�...

 

 

Stan Sakai

Pour les articles homonymes, voir Sakai (homonymie). Cet article est une ébauche concernant un auteur américain de bande dessinée. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Stan SakaiStan SakaiBiographieNaissance 25 mai 1953 (70 ans)KyotoNationalité américaineFormation Université d'HawaïKaimuki High School (en)Activités Auteur de bande dessinée, auteur de bande dessinéeAutres informationsSit...

 

 

José Manuel García-Margallo

Spanish politician In this Spanish name, the first or paternal surname is García-Margallo and the second or maternal family name is Marfil. José Manuel García-MargalloMinister of Foreign Affairs and CooperationIn office22 December 2011 – 4 November 2016Prime MinisterMariano RajoyPreceded byTrinidad JiménezSucceeded byAlfonso DastisMember of the Congress of DeputiesIn office13 January 2016 – 21 May 2019ConstituencyAlicanteIn office22 June 1986 – 19 ...

Verzetsmuseum

Museum in Plantage, Amsterdam, the Netherlands This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Verzetsmuseum – news · newspapers · books · scholar · JSTOR (July 2014) (Learn how and when to remove this message) VerzetsmuseumVerzetsmuseum in 2005Location in AmsterdamEstablished1999LocationPlantage Kerklaan 61...

 

 

Філософія

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

 

 

Colonial empire

Overseas possessions of a nation-state Colonial powers in 1898[a] A colonial empire is a collective of territories (often called colonies), either contiguous with the imperial center or located overseas, settled by the population of a certain state and governed by that state. Before the expansion of early modern European powers, other empires had conquered and colonized territories, such as the Roman Empire in Iberia, or the Chinese in what is now South China. Modern colonial empires ...

AT&T SportsNet

Defunct group of regional sports television networks Root Sports redirects here. For the channel in Seattle, Washington, see Root Sports Northwest. Television channel AT&T Sports Networks, LLCCountryUnited StatesBroadcast areaNationwide (through regional affiliates)HeadquartersAtlanta, GeorgiaProgrammingLanguage(s)EnglishPicture format720p (HDTV)480i (SDTV)OwnershipOwnerWarner Bros. DiscoveryParentTNT SportsSister channels HBO TBS TNT MLB Network NBA TV Motor Trend HistoryLaunchedMay ...

 

 

Wheel theory

Algebra where division is always defined A diagram of a wheel, as the real projective line with a point at nullity (denoted by ⊥). A wheel is a type of algebra (in the sense of universal algebra) where division is always defined. In particular, division by zero is meaningful. The real numbers can be extended to a wheel, as can any commutative ring. The term wheel is inspired by the topological picture ⊙ {\displaystyle \odot } of the real projective line together with an extra point �...

 

 

مارتن فيرغسون

مارتن فيرغسون معلومات شخصية الميلاد 21 ديسمبر 1942 (82 سنة)  غلاسكو  مركز اللعب مهاجم الجنسية المملكة المتحدة  معلومات النادي النادي الحالي أردريونيانز (chairman) مسيرة الشباب سنوات فريق درامتشابل أماتورز [الإنجليزية]‏ 000?–1962 Kirkintilloch Rob Roy F.C. [الإنجليزية]‏ المسيرة...

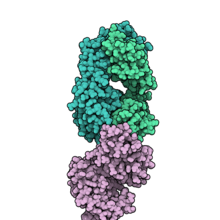
Daratumumab

Monoclonal antibody DaratumumabFab fragment of daratumumab (teal/green) binding CD38 (pale pink). From PDB entry 7DHAMonoclonal antibodyTypeWhole antibodySourceHumanTargetCD38Clinical dataTrade namesDarzalex, Darzalex SCAHFS/Drugs.comMonographMedlinePlusa616002License data US DailyMed: Daratumumab Pregnancycategory AU: C Routes ofadministrationIntravenous, subcutaneousATC codeL01FC01 (WHO) Legal statusLegal status AU: S4 (Prescription only)[1][2] ...

 

 

Chen Gong

Cet article est une ébauche concernant l’histoire et la Chine. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Chen GongBiographieNaissance Weizhou (d)Décès 7 février 199Activité Homme politiquemodifier - modifier le code - modifier Wikidata Chen Gong (154 - 198/7 février 199) est un conseiller de Lu Bu, qui finit exécuté en même temps que son maitre. Histoire Alors qu’il est magistrat de Zhongmou, ...

 

 

Площадь Революции (станция метро, Москва)

У этого термина существуют и другие значения, см. Площадь Революции. «Площадь Революции» Арбатско-Покровская линияМосковский метрополитен  Выявленный объект культурного наследия № 37329190№ 37329190 Выход на поверхность 55°45′23″ с. ш. 37°37′09″ в. д.HGЯO 55°45′23″ с.&#...

Cytochrome

Un exemple de cytochrome : le cytochrome c. Les cytochromes sont des coenzymes intermédiaires de la chaîne respiratoire. Ils ont comme caractéristique commune d'être constitués d'une porphyrine complexée avec un atome de fer ou de cuivre. C'est ce dernier qui confère au coenzyme ses propriétés oxydoréductrices en changeant de valence. Le couple oxydant/réducteur est le suivant : F e 2 + ↔ F e 3 + + e − {\displaystyle {\rm {Fe^{2+}\leftrightarrow Fe^{3+}+e^{-...

 

 

Iriseren

Iriserend oppervlak van zeepbellen Goudwesp Morpho didius Iriserende wolk Schelpen van slakken als de zeeoor (Haliotis) worden verwerkt tot sieraden. Labradoriet Iriseren (Grieks: iris = regenboog, ook iridiseren) is het natuurkundige verschijnsel van hoek-afhankelijke kleur en komt alleen voor bij structurele kleuren. Iriserende kleuren zijn het gevolg van breking en interferentie van licht in of aan het oppervlak van een voorwerp dat bestaat uit verschillende lagen met verschillende breking...