نظرية الزمر
|
Read other articles:
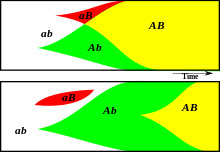
Fisherian explanation of the evolution of sexual reproduction and recombination This diagram illustrates how sexual reproduction (top) might create new genotypes faster than asexual reproduction (bottom). The advantageous alleles A and B occur randomly. In sexual reproduction, the two alleles are combined rapidly. But in asexual reproduction, the two alleles must independently arise through clonal interference. The Vicar of Bray hypothesis (or Fisher-Muller Model[1]) attempts to expla...

KekeyiLahirRahmawati Kekeyi Putri Cantikka17 Maret 1995 (umur 28)Nganjuk, Jawa Timur, IndonesiaPekerjaanSelebriti internetYoutuberpenyanyiaktorTahun aktif2018–sekarangTinggi136 cm (4 ft 6 in)[1]Orang tuaAida Fara (ibu)Karier musikGenrePopdanceInstrumenVokalTahun aktif2020–sekarangInformasi YouTubeKanal rahmawati kekeyi putri cantikka Tahun aktif2018–sekarangGenreTata riasmukbangblog videomusikPelanggan1.15 juta[2]Total tayang156 juta&#...

Lisbon DistrictDistrictCountryPortugalRegionLisbon(partly Alentejo Region)Historical provinceEstremadura Province(partly Ribatejo Province)No. of municipalities16No. of parishes226CapitalLisbonLuas • Total2,800 km2 (1,081 sq mi)Populasi • Total2.135.992 • Kepadatan0,76/km2 (2,0/sq mi)No. of parliamentary representatives47 Distrik Lisboa (pengucapan bahasa Portugis: [liʒˈβoɐ], Portugis: Distrito de Lisboacode: pt is deprecated )...

Pancreatic polypeptide cells (PP cells), or formerly as gamma cells (γ-cells), or F cells, are cells in the pancreatic islets (Islets of Langerhans) of the pancreas. Their main role is to help synthesize and regulate the release of pancreatic polypeptide (PP), after which they have been named. The pancreatic islets, where PP cells reside, was discovered in 1869 by a German pathological anatomist and scientist, Paul Langerhans. PP cells help to make up the pancreas but are smallest in proport...

Pemburu-pengumpul di Botswana. Pemburu-pengumpul adalah suatu masyarakat yang metode bertahan hidup utamanya adalah dengan cara berjelajah mencari hewan buruan dan mengumpulkan serangga ataupun tumbuh-tumbuhan liar yang dapat dimakan, tanpa adanya usaha-usaha yang nyata untuk membudidayakannya (domestikasi) terlebih dahulu.[1][2] Komunitas pemburu-pengumpul bertolak belakang dengan komunitas agraria menetap, yang utamanya mengandalkan pertanian dan peternakan untuk menghasilka...

بوي دي دوم علم شعار الاسم الرسمي (بالفرنسية: Puy-de-Dôme) الإحداثيات 45°42′00″N 3°13′00″E / 45.7°N 3.2166666666667°E / 45.7; 3.2166666666667 [1] تاريخ التأسيس 4 مارس 1790 تقسيم إداري البلد فرنسا[2][3] التقسيم الأعلى أوفرن-رون ألب (1 يناير 2016–) العاصم...

Questa voce o sezione sull'argomento centri abitati dell'Emilia-Romagna non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Castelnuovo Rangonecomune Castelnuovo Rangone – Veduta LocalizzazioneStato Italia Regione Emilia-Romagna Provincia Modena AmministrazioneSindacoMassimo Paradisi (centro-sinistra) dall'11-6-2017 TerritorioCoordinat...

Questa voce o sezione sull'argomento matematica non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Grafico della funzione y=cot(x) La cotangente di un angolo acuto corrisponde al rapporto fra il cateto ad esso adiacente e quello opposto In matematica, in particolare in trigonometria, la cotangente di un ango...

Japanese light novel series Koi wa Futago de WarikirenaiFirst light novel volume cover恋は双子で割り切れないGenreRomantic comedy[1] Light novelWritten byShihon TakamuraIllustrated byAlmicPublished byASCII Media WorksImprintDengeki BunkoDemographicMaleOriginal runMay 8, 2021 – presentVolumes5 MangaWritten byShihon TakamuraIllustrated byOkariPublished byASCII Media WorksImprintDengeki Comics NEXTMagazineComic Dengeki Daioh g [ja]De...

Main museum of Dubai Al Fahidi Fort redirects here. For the horse race, see Al Fahidi Fort (horse race). Dubai MuseumLocation within United Arab EmiratesEstablished1971LocationAl Fahidi Fort, Dubai, UAECoordinates25°15′47″N 55°17′50″E / 25.26306°N 55.29722°E / 25.26306; 55.29722TypeCovers the archaeology and history of Dubai, and a historic site by itselfVisitorsover 1 million (2013)Public transit accessAl Fahidi station, Dubai Metro Dubai Museum (Arabic: �...

Softball at the 2006 Asian GamesVenueAl-Rayyan Baseball & Softball VenueDates10–14 December 2006Competitors75 from 5 nations← 20022010 → Softball was contested by five East Asian countries at the 2006 Asian Games at Doha, Qatar from December 10 to December 14, 2006. All games were played at the Al-Rayyan Baseball and Softball Venue. Schedule P Preliminary round ½ Semifinals F Final G Grand final Event↓/Date → 10thSun 11thMon 12thTue 13thWe...

2015 film by J. J. Abrams For the film's soundtrack, see Star Wars: The Force Awakens (soundtrack). Star Wars: The Force AwakensTheatrical release posterDirected byJ. J. AbramsWritten by Lawrence Kasdan J. J. Abrams Michael Arndt Based onCharactersby George LucasProduced by Kathleen Kennedy J. J. Abrams Bryan Burk Starring Harrison Ford Mark Hamill Carrie Fisher Adam Driver Daisy Ridley John Boyega Oscar Isaac Lupita Nyong'o Andy Serkis Domhnall Gleeson Anthony Daniels Peter Mayhew Max von Sy...

AIMS can be used to identify five European clusters In population genetics, an ancestry-informative marker (AIM) is a single-nucleotide polymorphism that exhibits substantially different frequencies between different populations. A set of many AIMs can be used to estimate the proportion of ancestry of an individual derived from each population. A single-nucleotide polymorphism is a modification of a single nucleotide base within a DNA sequence.[1] There are an estimated 15 million SNP...

ピタゴラスの定理 種類 定理分野 ユークリッド幾何学命題 2辺 (a, b) 上の2つの正方形の面積の和は、斜辺 (c) 上の正方形の面積に等しくなる。数式 a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}} 一般化 余弦定理 空間幾何学 非ユークリッド幾何学 微分幾何学 結果 ピタゴラス数 逆ピタゴラスの定理 複素数 ユークリッド距離 ピタゴラスの三角恒等式 初等幾何学におけるピタゴラ�...

Indian government agency Directorate of Film FestivalsFormation1973TypeGovernment AgencyPurposeTo organise International and National Film Festivals in IndiaHeadquartersSiri Fort Auditorium Complex, New DelhiRegion served IndiaDirectorSenthil RajanParent organisationMinistry of Information and BroadcastingWebsitedff.gov.in The Directorate of Film Festivals in India was an organisation that initiated and presented the International Film Festival of India, the National Film Awards and the India...

City in California, United States For other places in California named Mountain View, see Mountain View (disambiguation). City in California, United StatesMountain View, CaliforniaCityCity Hall & Performing Arts Center FlagSealLocation within Santa Clara CountyMountain View city map, California, U.S.Coordinates: 37°23′10″N 122°05′02″W / 37.38611°N 122.08389°W / 37.38611; -122.08389CountryUnited StatesStateCaliforniaCountySanta ClaraIncorporatedNovember ...

2002 greatest hits album by BjörkGreatest HitsStandard cover[a]Greatest hits album by BjörkReleased4 November 2002Recorded1993–2002GenreElectropop[1]Length72:19LabelOne Little IndianProducer Björk Nellee Hooper Mark Bell Graham Massey David Arnold Danny Cannon Drew Daniel Björk chronology Vespertine(2001) Greatest Hits(2002) Family Tree(2002) Singles from Greatest Hits It's in Our HandsReleased: 9 November 2002 Professional ratingsReview scoresSourceRatingAllmusi...

United States historic placeBoonton Historic DistrictU.S. National Register of Historic PlacesU.S. Historic districtNew Jersey Register of Historic Places Garret Rickards House, an octagon houseShow map of Morris County, New JerseyShow map of New JerseyShow map of the United StatesLocationMain, Church, Birch, Cornelia, and Cedar StreetsBoonton, New JerseyCoordinates40°54′22″N 74°24′37″W / 40.90611°N 74.41028°W / 40.90611; -74.41028 (Boonton Histori...

Structure of a bridge The pier of a bridge is an intermediate support that holds the deck of the structure. It is a massive and permanent support, as opposed to the shoring, which is lighter and provides temporary support.[1] History Fades viaduct – The tallest traditional masonry piers ever built (92 m). Until the advent of concrete and the use of cast iron and then steel, bridges were made of masonry. Roman bridges were sturdy, semicircular, and rested on thick piers, with a width...

Mirror canon[1] The mirror canon (also called a canon by contrary motion) is a type of canon which involves the leading voice being played alongside its own inversion (i.e. upside-down). The realisation from the 'closed' (unrealised) form can be effected by placing the page in front of a mirror, thus upside down, and beginning with the already progressing first voice. The Canon a 2 'Quaerendo invenietis' from J. S. Bach's The Musical Offering, BWV 1079, is a fine example of the proces...






