عددان أوليان توأم
|
Read other articles:

David Villa David Villa con la nazionale spagnola nel 2013 Nazionalità Spagna Altezza 175[1] cm Peso 78[1] kg Calcio Ruolo Attaccante Termine carriera 1º febbraio 2020 Carriera Giovanili 1991-1999 Langreo Squadre di club1 1999-2001 Sporting Gijón B66 (26)2001-2003 Sporting Gijón80 (38)2003-2005 Real Saragozza73 (32)2005-2010 Valencia166 (108)2010-2013 Barcellona77 (33)2013-2014 Atlético Madrid36 (13)2014→ Melbourne City ...

بيراندرا ملك نيبال (بالنيبالية: वीरेन्द्र वीर विक्रम शाहदेव) معلومات شخصية الميلاد 28 ديسمبر 1945(1945-12-28)كاثماندو الوفاة 1 يونيو 2001 (55 سنة)كاثماندو سبب الوفاة قتل الأب أو الأم قتله ديبندار بيكرام مواطنة نيبال الزوجة الأميرة أيشواريا ملكة نيبال الأولاد ...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: The Duck Variations – news · newspapers · books · scholar · JSTOR (August 2011) The Duck Variations is a 1972 play by American playwright David Mamet. The play depicts a discussion taking place between two elderly men sitting on a park bench watching ...

Festival Film Indonesia ke-33Tanggal7 Desember 2013 (2013-12-07)TempatMarina Convention Center, Semarang, Jawa TengahPembawa acaraAndhika PratamaGading MartenNirina ZubirSorotanFilm TerbaikSang KiaiPenyutradaraan TerbaikRako PrijantoSang KiaiAktor TerbaikReza RahadianHabibie & AinunAktris TerbaikAdinia WirastiLaura & MarshaPenghargaan terbanyakSang Kiai (4)Nominasi terbanyakLaura dan Marsha (11)Liputan televisiSaluranSCTVDurasi180 menit ← 2012 Festival Film Indonesia 2...

Voce principale: Turn- und Sportgemeinschaft 1899 Hoffenheim. Turn- und Sportgemeinschaft 1899 HoffenheimStagione 1898-1899Sport calcio Squadra Hoffenheim Allenatore Alfred Schreuder (1ª-30ª) Matthias Kaltenbach (31ª-34ª) All. in seconda Kai Herdling Bundesliga6º posto Coppa di GermaniaOttavi di finale Maggiori presenzeCampionato: Rudy, Bebou (32)Totale: Rudy, Bebou (35) Miglior marcatoreCampionato: Kramarić (12)Totale: Kramarić (12) StadioPreZero Arena Maggior numero di spettato...

Salib Pasar, dibangun pada 1814 untuk menggantikan salib sebelumnya yang berdiri sedikit ke selatan[1] Devizes /dɪˈvaɪzɪz/ merupakan kota pasar dan paroki sipil di Wiltshire, Inggris. Kota ini berkembang di sekitar Puri Devizes, sebuah puri Norman abad ke-XI,[2] dan menerima piagam pada 1141. Puri itu dikepung selama The Anarchy, perang saudara abad ke-XII antara Stephen dari Inggris dan Matilda dari Inggris, dan lagi selama Perang Saudara Inggris ketika Cavalier mengangka...

Belgian artistic gymnast Some of this article's listed sources may not be reliable. Please help improve this article by looking for better, more reliable sources. Unreliable citations may be challenged and removed. (November 2020) (Learn how and when to remove this message) Aagje VanwalleghemAagje Vanwalleghem in 2004Personal informationFull nameAagje Vanwalleghem(formerly Ana Maria Pereira da Silva)Country representedBelgiumBorn (1987-10-24) 24 October 1987 (age 36)Poção de Pedra...

Atikamekw on the dock of the Hudson's Bay Company on the Obedjiwan Lake circa 1921 The Atikamekw of Opitciwan (French: Atikamekw d'Opitciwan) are an Atikamekw First Nation in Quebec, Canada. In 2016, it has a registered population of 2,937 members,[1] who live primarily on an Indian reserve, Obedjiwan 28, located in Mauricie.[2] References ^ Registered Population. Crown–Indigenous Relations and Northern Affairs Canada. Government of Canada. Retrieved 29 November 2016.. ^ Res...

This article is about the district in Worcestershire. For the ancient woodland, see Wyre Forest. For the district in Lancashire, see Borough of Wyre. Non-metropolitan district in EnglandWyre ForestNon-metropolitan districtKidderminster, the district's largest town and administrative centreWyre Forest shown within WorcestershireSovereign stateUnited KingdomConstituent countryEnglandRegionWest MidlandsNon-metropolitan countyWorcestershireStatusNon-metropolitan districtAdmin HQKidderminsterIncor...

烏克蘭總理Прем'єр-міністр України烏克蘭國徽現任杰尼斯·什米加尔自2020年3月4日任命者烏克蘭總統任期總統任命首任維托爾德·福金设立1991年11月后继职位無网站www.kmu.gov.ua/control/en/(英文) 乌克兰 乌克兰政府与政治系列条目 宪法 政府 总统 弗拉基米尔·泽连斯基 總統辦公室 国家安全与国防事务委员会 总统代表(英语:Representatives of the President of Ukraine) 总...

Second Board of Ministers23rd Cabinet of British CeylonDate formedMarch 1936Date dissolvedJune 1947People and organisationsHead of stateEdward VIIIGeorge VIHead of governmentGuy Stanley Wodeman (1940–42)Robert DraytonDeputy head of governmentDon Baron Jayatilaka (1936–42)D. S. Senanayake (1942–47)Ministers removed5Total no. of members15HistoryElection(s)1936Outgoing election1947Legislature term(s)2ndPredecessorFirst Board of MinistersSuccessorD. S. Senanayake cabinet The Second Board o...

Beauty pageant Miss France 2011Laury ThillemanDate4 December 2010PresentersJean-Pierre FoucaultVenueZénith de Caen, CaenBroadcasterTF1Entrants33Placements12DebutsMiss CentreWithdrawalsMiss Albigeois Midi-Pyrénées, Artois Hainaut, Miss Béarn-Gascogne, Miss Berry Val de Loire, Miss Flandre, Miss Loire Forez, Miss Paris, Miss Quercy RouergueReturnsMiss Midi-Pyrénées, Miss New Caledonia, Miss Nord-Pas-de-CalaisWinnerLaury Thilleman BrittanyCongenialityJulie-Malika Grosse French ...

◄◄ ◄ 16 november ► ►► Veckodag 2024: Lördag Okt · November · Dec Årets 320:e dag(321:a under skottår)45 dagar till årets slut Må Ti On To Fr Lö Sö 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 2024 Alla datum Månader Januari • Februari • Mars April • Maj • Juni • Juli Augusti • September • Oktober November • December På Wikimedia Commonsfinns...

American politician and educator Erin MurphyMurphy in 2024Member of the Boston City Councilat-largeIncumbentAssumed office December 1, 2021Preceded byMichelle Wu Personal detailsBorn1969 or 1970 (age 53–54)[1]Political partyDemocraticChildren4Website Government webpage Campaign website Erin J. Murphy is an American politician and educator who has served as an at-large member of the Boston City Council since December 2021. Murphy is a Democrat, and is considered ...
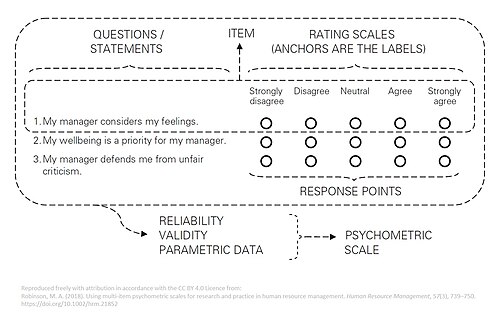
Design of a questionnaire to gather statistically useful information about a given topic Questionnaire construction refers to the design of a questionnaire to gather statistically useful information about a given topic. When properly constructed and responsibly administered, questionnaires can provide valuable data about any given subject. Questionnaires Main article: Questionnaire Questionnaires are frequently used in quantitative marketing research and social research. They are a valuable m...

Italian football manager (born 1957) Giuseppe Sannino Beppe Sannino in 2014.Personal informationDate of birth (1957-04-30) 30 April 1957 (age 67)Place of birth Ottaviano, ItalyPosition(s) MidfielderTeam informationCurrent team FC Paradiso (head coach)Senior career*Years Team Apps (Gls)1975–1976 Varese 0 (0)1976–1977 Milanese 1920 ? (?)1977–1979 Trento 51 (6)1979–1982 Vogherese 65 (18)1982–1984 Fanfulla 64 (6)1984 Pavia 0 (0)1984–1985 Spezia 24 (1)1985–1986 Vogherese 34 (0)1...

Soviet Russian footballer and coach Valentin Nikolayev Personal informationFull name Valentin Aleksandrovich NikolayevDate of birth August 16, 1921 (1921-08-16)Place of birth Yerosovo, Vladimir Governorate, USSRDate of death October 9, 2009 (2009-10-10) (aged 88)Place of death MoscowHeight 1.72 m (5 ft 8 in)Position(s) ForwardYouth career Kazanka MoscowSenior career*Years Team Apps (Gls)1940–1952 CDKA Moscow 187 (79)1952 Kalinin City Team 4 (2)1953 MVO Moscow 0...

Norwegian jazz singer and composer Kristin AsbjørnsenKristin Asbjørnsen performing at the 2019 Jazz på Jølst festivalBackground informationBorn (1971-05-12) 12 May 1971 (age 53)Lillehammer, NorwayOriginNorwayGenresJazzOccupation(s)Musician, composer, band leaderInstrumentVocalsWebsiteOfficial websiteMusical artist Kristin Asbjørnsen (born 12 May 1971) is a Norwegian jazz singer and composer whose focus is on improvised music. She is known for musical projects like Dadafon including ...

American football player (born 1983) American football player Chris ReisNo. 39Position:SafetyPersonal informationBorn: (1983-09-19) September 19, 1983 (age 41)Roswell, Georgia, U.S.Height:6 ft 1 in (1.85 m)Weight:210 lb (95 kg)Career informationHigh school:Roswell (GA)College:Georgia TechUndrafted:2006Career history Atlanta Falcons (2006)* Cologne Centurions (2007) New Orleans Saints (2007–2010) * Offseason and/or practice squad member only Career highlig...

新渡戸 稲造 人物情報別名 太田稲造生誕 新渡戸稲之助文久2年8月3日(1862年9月1日) 日本陸奥国岩手郡盛岡死没 (1933-10-15) 1933年10月15日(71歳没) カナダブリティッシュコロンビア州ビクトリア国籍 日本出身校 ハレ大学 札幌農学校 東京英語学校 作人館 配偶者 メアリー・エルキントン(新渡戸万里子)両親 父:新渡戸十次郎子供 遠益 こと 学問研究分野 農学 農業経済�...



































