رياضيات بحتة
|
Read other articles:

Strada statale 109 bis-dir/Adell'Ospedale di CatanzaroLocalizzazioneStato Italia Regioni Calabria Province Catanzaro DatiClassificazioneStrada statale InizioInnesto su S.S. n. 109 bis FineInnesto con la S.C. Viale Papa Pio X Lunghezza0,724 km GestoreANAS Manuale La strada statale 109 bis-dir/A dell'Ospedale di Catanzaro (SS 109 bis-dir/A) è una strada statale italiana. Percorso La strada statale 109 bis-dir/A, gestita dal Compartimento di Catanzaro, ha inizio dalla SS 109 bis ...
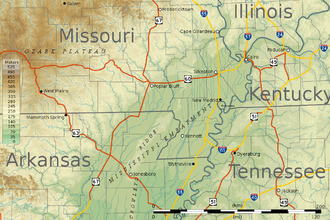
For other uses, see Bootheel. PlaceMissouri BootheelLocation of the bootheel region centered on 36°15′N 89°51′W / 36.250°N 89.850°W / 36.250; -89.850Area[1] • Land1,708.45 sq mi (4,424.9 km2)Population (2019)[2] • Total62,012 • Density36.3/sq mi (14.0/km2) Topographic map of the bootheel and surrounding areas of Missouri and neighboring states. The Missouri Bootheel is a salient (protr...

خريطة سويسرا بالعلم السويسري الشعار الرسمي للاتحاد السويسري 1470–1798 1798–1803 1803–1815 1815–1848 1889–حتى الآن راية سويسرا بازل. برن. جنيف. لوزان. ســــويــــســـــرا(بالألمانية:die Schweiz، بالفرنسية:la Suisse، بالإيطالية:Svizzera، بالرومانشية:Svizra) أو الاتحاد السويسري هي جمهورية فيدرالية تتكو�...

Talas Klasifikasi ilmiah Kerajaan: Plantae (tanpa takson): Angiospermae (tanpa takson): Monokotil Ordo: Alismatales Famili: Araceae Genus: Colocasia Spesies: C. esculenta Nama binomial Colocasia esculenta(L.) Schott[1] Sinonim Arum esculentum L., 1753[2] (basionym) Colocasia antiquorum Schott sinonim lain, lihat pada The Plant List[3] Talas, keladi, atau seratah (Colocasia esculenta L.) adalah tumbuhan penghasil umbi-umbian yang cukup penting. Tanaman ini berasal...

American racing driver (born 1969) NASCAR driver Hermie SadlerSadler (right) interviewing Christopher Bell at Kentucky Speedway in 2016BornHerman Marion Sadler III (1969-04-24) April 24, 1969 (age 55)Emporia, Virginia, U.S.Awards1993 NASCAR Busch Series Rookie of the YearNASCAR Cup Series career66 races run over 12 years2018 position50thBest finish44th (2004, 2005)First race1996 Miller 500 (Dover)Last race2018 First Data 500 (Martinsville) Wins Top tens Poles 0 0 0 NASCAR Xfinity Series ...

American animated short film series This article is about the short film series starring Goofy. For the duology of feature films starring the character, see A Goofy Movie and An Extremely Goofy Movie. GoofyIntroductory title of the Goofy short film series.ProductioncompaniesWalt Disney Productions (1-44)Walt Disney Pictures (45)Walt Disney Animation Studios (45)Distributed byRKO Radio Pictures (1-44)[a]Walt Disney Studios Motion Pictures (45)CountryUnited StatesLanguageEnglish Goofy i...

College of the University of Oxford St Hilda's CollegeOxfordSouth BuildingArms: Azure, on a fess or three estoiles gules in chief two unicorns' heads couped, in base a coiled serpent argent. LocationCowley PlaceCoordinates51°44′57″N 1°14′43″W / 51.749162°N 1.245334°W / 51.749162; -1.245334Latin nameCollegium Sanctae HildaeMottonon frustra vixi (I lived not in vain)Established1893Named for...

Geografi Ptolemaeus dalam sebuah terjemahan Latin sekitar tahun 1411 oleh Jacobus Angelus dengan 27 peta oleh Claus Swart. Geografi (bahasa Yunani Kuno: Γεωγραφικὴ Ὑφήγησις, Geōgraphikḕ Hyphḗgēsis, lit. Panduan Geografi), juga dikenal dalam bahasa Latin Geographia dan disebut juga Cosmographia, adalah gazetir, atlas, risalah kartografi, dan kumpulan ilmu pengetahuan geografi pada zaman Kekaisaran Romawi. Pertama kali ditulis oleh Klaudius Ptolemaeus dalam ba...

关于与「友谊勋章 (俄罗斯)」標題相近或相同的条目页,請見「友谊勋章 (消歧义)」。 友谊勋章类型单级勋章(仅设有一个等级)授予原因加强各民族友谊、交流与合作国家/地区俄罗斯 颁发单位 俄羅斯颁授资格俄罗斯国民及世界各民族人民設立時間1994年3月2日[1]首次颁发康斯坦丁·蒂托夫(萨马拉州州长)绶带 优先顺序上等荣誉勋章下等光荣父母�...

1974 biography of Robert Moses by Robert Caro For other uses, see Power broker. The Power Broker Cover art of The Power Broker since publicationAuthorRobert CaroCountryUnited StatesLanguageEnglishSubjectRobert MosesGenreBiographyPublisherKnopfPublication dateSeptember 16, 1974[1]Media typeHardback, PaperbackPages1,336ISBN0-394-72024-5OCLC1631862Dewey Decimal974.7/04/0924 BLC ClassNA9085.M68 C37 1975 The Power Broker: Robert Moses and the Fall of New York is a 1974 biography ...

Alexander Calder Alexander Calder (Lawnton, 22 luglio 1898 – New York, 11 novembre 1976) è stato uno scultore statunitense. Alexander Calder 1968. È famoso per l'invenzione di grandi sculture di arte cinetica chiamate mobile. Oltre alle opere di scultura, mobile e stabile, Alexander Calder si dedicò anche alla pittura, alle litografie e alla progettazione di giocattoli, arazzi, tappeti e gioielli. Indice 1 Biografia 2 Carriera artistica 2.1 Il Circo Calder - Le Mobiles 2.2 Le Stabiles 2....

Pillards gaulois par Évariste-Vital Luminais. Musée de la société historique et archéologique de Langres. Le terme « bagaudes » (en latin : bagaudæ et bacaudæ, nom masculin pluriel) désigne à l'époque de l'empire romain tardif des mouvements insurrectionnels intermittents de type jacquerie, sous forme de bandes armées de paysans sans terre, d'esclaves, de soldats déserteurs et de brigands, actives principalement en Gaule à partir de la fin du IIIe siècle, p...
Рейхспочта Членство отсутствует Административный центр Берлин Локация Германский рейх Тип организации государственное учреждение Основание Дата основания 1866 Ликвидация 1945 Листинг на бирже отсутствовал Отрасль почта Продукция почтовые услуги Материнская организ...

Questa voce sull'argomento cestisti cecoslovacchi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Alena KopeckáNazionalità Cecoslovacchia Altezza181 cm Pallacanestro Termine carriera1988 CarrieraSquadre di club 1973-1988 Sparta Praga Nazionale 1976-1984 Cecoslovacchia200 Palmarès Europei BronzoPolonia 1978 BronzoItalia 1981 Il simbolo → indica un trasferimento in prestito. M...

City in Illinois, United StatesMount Vernon, IllinoisCityTown Center of Mount VernonNickname(s): The King City, The Festival CityMotto(s): Mount Vernon, City of Opportunity[1]Location of Mount Vernon in Jefferson County, Illinois.Mount VernonShow map of IllinoisMount VernonShow map of the United StatesCoordinates: 38°19′02″N 88°55′02″W / 38.31722°N 88.91722°W / 38.31722; -88.91722[2]CountryUnited StatesStateIllinoisCountyJefferson...

Sporting event delegationNepal at the1980 Summer OlympicsIOC codeNEPNOCNepal Olympic CommitteeWebsitewww.nocnepal.org.npin MoscowCompetitors13Medals Gold 0 Silver 0 Bronze 0 Total 0 Summer Olympics appearances (overview)1964196819721976198019841988199219962000200420082012201620202024 Nepal competed at the 1980 Summer Olympics in Moscow, USSR. Results by event Athletics Men's 100 metres Raghuraj Onta Heat — 11.61 (→ did not advance) Men's 5,000 metres Laxman Basnet Heat — 16:11.7...

Political party in Poland This article is about the current political party. For other uses, see Polish People's Party (disambiguation). Polish People's Party Polskie Stronnictwo LudoweLeaderWładysław Kosiniak-KamyszFounded1895 (original form)1990 (current form)Merger ofPolish People's PartyPolish People's Party RebirthRural SolidarityPolish People's Party SolidarityPreceded byUnited People's PartyHeadquartersul. Kopernika 36/40, 00-924 WarsawMembership (2023) 73,222[1]Ide...

Belarusian ice dancer Yurii BieliaievKavaliova/Bieliaiev in 2012Other namesYirii Bieliaiev[1]Born (1992-11-04) 4 November 1992 (age 31)Odesa, UkraineHometownMinsk, BelarusHeight1.95 m (6 ft 5 in)Figure skating careerCountryBelarusPartnerViktoria KavaliovaCoachNikolai Morozov, Alexei Gorshkov, Tatiana BieliaevaSkating clubRCOP MinskBegan skating1996Retired2018 Yurii Bieliaiev (born 4 November 1992) is a Belarusian former competitive ice dancer. With partner Viktoria...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. Artikel atau sebagian dari artikel ini mungkin diterjemahkan dari Russian gay propaganda law di en.wikipedia.org. Isinya masih belum akurat, karena bagian yang diterjemahkan masih perlu diperhalus dan disempurnakan. Jika Anda menguasai bahasa aslinya, ...

Arabic variety spoken predominantly in the Algerian Sahara Not to be confused with Algerian Arabic. Algerian Saharan ArabicSaharan ArabicTamanrasset ArabicTamanghasset ArabicNative toAlgeria[1]RegionAtlas Mountains, southern SaharaSpeakers310,000 (2022)[1]Language familyAfro-Asiatic SemiticWest SemiticCentral SemiticArabicMaghrebiAlgerian Saharan ArabicLanguage codesISO 639-3aaoGlottologalge1240[image reference needed]Algerian Saharan Arabic (also known as Sa...
