تاريخ الجبر
|
Read other articles:

Berkelium tetrafluorida Nama Nama lain Berkelium(IV) fluorida Penanda Nomor CAS 22422-27-1 Model 3D (JSmol) Gambar interaktif 3DMet {{{3DMet}}} Nomor EC Nomor RTECS {{{value}}} InChI InChI=1S/Bk.4FH/h;4*1H/q+4;;;;/p-4Key: RCTCKHUWZHELJP-UHFFFAOYSA-J SMILES [Bk+4].[F-].[F-].[F-].[F-] Sifat Rumus kimia BkF4 Massa molar 322,99 g·mol−1 Penampilan Padatan kuning kehijauan Kelarutan dalam air Tak larut Struktur Struktur kristal Monoklinik Senyawa terkait Senyawa terkait Kurium ...

Irfan Bachdim Irfan Bachdim saat membela Bali UnitedInformasi pribadiNama lengkap Irfan Haarys BachdimTanggal lahir 11 Agustus 1988 (umur 35)Tempat lahir Amsterdam, BelandaTinggi 175 cm (5 ft 9 in)Posisi bermain Gelandang, penyerangInformasi klubKlub saat ini Persik KediriNomor 5Karier junior1997–1998 SV Argon1998–2000 Ajax Amsterdam2000–2003 SV Argon2003–2007 FC UtrechtKarier senior*Tahun Tim Tampil (Gol)2007–2009 FC Utrecht 1 (0)2009–2010 HFC Haarlem 12 (2)2...

[1] Cave and archaeological site in France Pech MerlePrehistoric cave artLocationLot Department, Midi-Pyrénées, FranceCoordinates44°30′27″N 1°38′40″E / 44.5074288°N 1.6443131°E / 44.5074288; 1.6443131 Pech Merle is a cave which opens onto a hillside at Cabrerets in the Lot département of the Occitania region in France, about 32 km by road east of Cahors. It is one of the few prehistoric cave painting sites in France that remain open to the g...

Nagios Capture d'écran de l'interface web de Nagios. Informations Développé par Ethan Galstad et d'autres Première version 1996[1] Dernière version 4.5.1 (28 février 2024)[2] Dépôt github.com/NagiosEnterprises/nagioscore Écrit en Perl et C Système d'exploitation Type Unix Environnement Linux, *NIX Langues Anglais Type Network monitoring Licence Licence publique générale GNU Site web www.nagios.org modifier - modifier le code - voir Wikidata (aide) L'utilisation de Nagios. Nagios ...

Diplomatic travel document issued by the United Nations United Nations laissez-passerThe front cover of a blue machine-readable United Nations laissez-passer.Typelaissez-passerIssued byUnited Nations and the International Labour OrganizationPurposeIdentificationEligibilityUN officials and officials of the United Nations Specialized Agencies and the IAEASize88 mm × 125 mm (3.5 in × 4.9 in) United Nations laissez-passerThe front cover of a red machine-readable Un...

Balai kota Slutskk Slutsk (Belarus: Слуцк) merupakan sebuah kota di Belarus. Kota ini letaknya di bagian tengah. Tepatnya di Voblast Minsk. Pada tahun 2010, kota ini memiliki jumlah penduduk sebesar 61.400 jiwa dan memiliki luas wilayah 24,6 km². Kota ini memiliki angka kepadatan penduduk 2.495 jiwa/km². Pranala luar Media terkait Sluck di Wikimedia Commons Home page of the city of Slutsk History of the Jewish Community of Slutsk The Historical Society of Slutsk Presents The Pinka...

Sexual entertainment venue Strip club in Munich, Germany A strip club is a venue where strippers provide adult entertainment, predominantly in the form of striptease or other erotic dances. Strip clubs typically adopt a nightclub or bar style, and can also adopt a theatre or cabaret-style. American-style strip clubs began to appear outside North America after World War II, arriving in Asia in the late 1980s and Europe in 1978,[1] where they competed against the local English and Frenc...

U.S. presidential administration from 1909 to 1913 Presidency of William Howard TaftMarch 4, 1909 – March 4, 1913CabinetSee listPartyRepublicanElection1908SeatWhite House← Theodore RooseveltWoodrow Wilson → Seal of the president(1894–1945) This article is part of a series aboutWilliam Howard Taft Early life Family Bibliography Legacy 27th President of the United States Inauguration Presidency (timeline) Executive actions Foreign policy Taftian theory Domesti...

Notable German Jewish family Moses Mendelssohn Fromet Mendelssohn née Guggenheim The Mendelssohn family are the descendants of Mendel of Dessau. The German Jewish philosopher Moses Mendelssohn and his brother Saul were the first to adopt the surname Mendelssohn. The family includes his grandson, the composer Felix Mendelssohn, and his granddaughter, the composer Fanny Mendelssohn. Moses Mendelssohn Moses Mendelssohn was a significant figure in the Age of Enlightenment in Germany. Mendelssohn...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府(Oguzkhan Presidential Palace)機關所在地阿什哈巴德任命者直接选举任期7年,可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關(英语:National Council of Turkmenistan) ...

3DES المطورون آي بي إم تاريخ النشر 1999 اشتقت من معيار تشفير البيانات تعديل مصدري - تعديل 3DES أو Triple DES هي خوارزمية تشفير كتل وقد ظهرت على أنها بديل للخوارزمية DES التي كانت رائجة وامنة ولكن وبعد أن أُخترقت كان هناك حاجة لبديل ولعل العيب الأساسي في DES هو ان طول م...

South Korean singer (born 1994) In this Korean name, the family name is Song. Song I-hanSong busking in Hongdae, 2022Background informationBirth nameSong Byeong-hwaAlso known asHwigyeong-dongBorn (1994-08-11) August 11, 1994 (age 29)Bucheon, South KoreaGenresR&BOccupationsSinger-songwriterInstrumentsVocalsYears active2018–presentLabelsMusic DesignKorean nameHangul송병화Revised RomanizationSong Byeong-hwaMcCune–ReischauerSong PyŏnghwaStage nameHangul송이한Revised Romanizati...

One of the 234 State Legislative Assembly Constituencies in Tamil Nadu, in India 9°58′N 77°48′E / 9.97°N 77.8°E / 9.97; 77.8 UsilampattiConstituency No. 197 for the Tamil Nadu Legislative AssemblyConstituency detailsCountryIndiaRegionSouth IndiaStateTamil NaduTotal electors2,84,585[1]Member of Legislative Assembly16th Tamil Nadu Legislative AssemblyIncumbent P. Ayyappan Party IndependentElected year2021 Usilampatti is a state assembly constit...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Maret 2016. SMK Negeri 1 GratiInformasiJurusan atau peminatanMM, KI, TPm, TPc, TAV, AK, ATug, dan APiAlamatLokasiJl. Raya Ngopak No. 1 Grati - Pasuruan, Jawa TimurMoto SMK Negeri (SMKN) 1 Grati, merupakan salah satu Sekolah Menengah Kejuruan Negeri yang ada di Kabup...
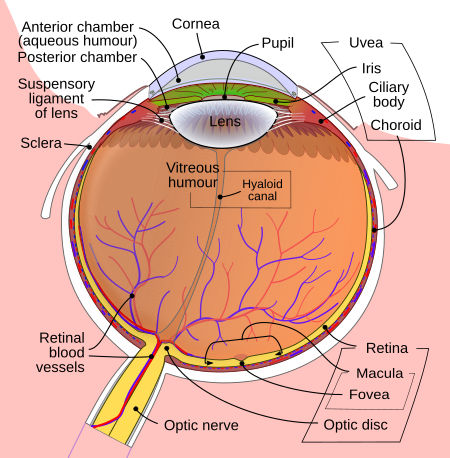
Fluid in the anterior segment of the eye Aqueous humourSchematic diagram of the human eye.DetailsIdentifiersLatinhumor aquosusMeSHD001082TA98A15.2.06.002TA26791FMA58819Anatomical terminology[edit on Wikidata] The aqueous humour is a transparent water-like fluid similar to blood plasma, but containing low protein concentrations. It is secreted from the ciliary body, a structure supporting the lens of the eyeball.[1] It fills both the anterior and the posterior chambers of the eye, ...

Territorio africano della prima guerra mondialeparte della prima guerra mondialeL'Africa nel 1913Data3 agosto 1914 - 23 novembre 1918 LuogoCamerun, Togo, Namibia, Tanzania, Zambia, Mozambico EsitoVittorie alleate in tutte le colonie, con l'eccezione dell'Africa Orientale (vittoria tattica tedesca) Schieramenti Impero britannico Sudafrica Australia Francia Belgio Italia Portogallo Germania Impero ottomanoSenussiRibelli marocchiniBoeri Voci di battaglie...

Stack It UpSingel oleh Liam Payne featuring A Boogie wit da Hoodiedari album LP1Dirilis18 September 2019 (2019-09-18)FormatUnduhan digitalstreamingGenrePopR&Bhip hop[1]Durasi2:46LabelCapitolPenciptaEd SheeranFred GibsonJulius DuboseSteve MacProduserSteve MacFred GibsonKronologi singel Liam Payne Polaroid (2018) Stack It Up (2019) All I Want (For Christmas) (2019) Kronologi singel A Boogie wit da Hoodie Mood Swings(2019) Stack It Up(2019) Stretch You Out(2019) Video ...

Elezioni regionali in Umbria del 1975Stato Italia Regione Umbria LegislaturaII Affluenza94,98% Seggi in Consiglio regionale PCI 14 / 30 DC 9 / 30 PSI 4 / 30 MSI-DN 1 / 30 PSDI 1 / 30 PRI 1 / 30 Distribuzione del voto per comune Presidenti della Giunta regionale:Pietro Conti (PCI) Germano Marri (PCI) 1970 1980 Le elezioni regionali in Umbria del 1975 si tennero il 15-16 giugno. Il presidente uscente. Pietro Conti è stato riconfermato alla carica di presidente. Rimarrà in carica fi...

Any significant alteration in societal order Social transition redirects here. For social adjustments as part of an individual's gender transition, see Gender transition § Social, psychological, and aesthetic aspects. Part of a series onSociology History Outline Index Key themes Society Globalization Human behavior Human environmental impact Identity Industrial revolutions 3 / 4 / 5 Popularity Social complexity Social environment Social equality Social equity Social power Social stratif...

Un dissident est une personne qui se sépare d'une communauté ou parti politique dont elle était membre. Le dissident ne reconnaît plus la légitimité de l'autorité (notamment politique) à laquelle il devait se soumettre jusqu'alors, et conteste de façon plus ou moins radicale le système politique du pays dont il est résident. Origine du terme Le terme « dissident » est assez ancien. Le mot vient du latin dis-sedere (« se séparer de » et « être assis&#...



