معادلة تربيعية
|
Read other articles:

Sumsum tulang belakang. Sumsum tulang belakang adalah saraf yang tipis yang merupakan perpanjangan dari sistem saraf pusat dari otak dan melengkungi serta dilindungi oleh tulang belakang. Fungsi utama sumsum tulang belakang adalah transmisi pemasukan rangsangan antara periferi dan otak. Fungsi lain sumsum tulang belakang adalah mengontrol gerakan refleks, termasuk gerakan reflek pada mata, hidung, dan lain-lain. Lihat pula Sumsum tulang Pranala luar Spinal Cord Histology Diarsipkan 2006-09-10...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يوليو 2019) ديلان سميث معلومات شخصية الميلاد 26 فبراير 1994 (30 سنة) ديربان مواطنة جنوب إفريقيا الحياة العملية المهنة لاعب اتحاد الرغبي اللغات الإنجليزية ال...

Distrik Jung 중구Distrik중구 · 中區SungryemunLokasi Jung-gu di SeoulRegionSudogwonKota IstimewaSeoulDong15Luas • Total9,96 km2 (385 sq mi)Populasi (2010[1]) • Total121.144 • Kepadatan0,12/km2 (0,32/sq mi)Zona waktuUTC+9 (Waktu Standar Korea)Situs webJung-gu official website Distrik Jung (Jung-gu), yang bermakna Distrik Pusat, adalah satu dari 25 distrik (gu) di Seoul, Korea Selatan. Distrik ini terletak di sisi utara ...

Malaysian corporate figure and civil servant (1935–2004) In this Malay name, there is no surname or family name. The name Zainul Abidin is a patronymic, and the person should be referred to by their given name, Azizan. The word bin or binti/binte means 'son of' or 'daughter of', respectively. Yang Amat Berbahagia TunAzizan Zainul AbidinSSM PSM JMN PNBS DGPNعزيزان زین العابدینPresident and Chief Executive Officer of PetronasIn officeFebruary 1988 – February...

Pamatang Silima HutaKecamatanKantor Kecamatan Pamatang SilimahutaPeta lokasi Kecamatan Pamatang Silima HutaNegara IndonesiaProvinsiSumatera UtaraKabupatenSimalungunPemerintahan • Camat-Populasi • Total- jiwaKode Kemendagri12.08.31 Kode BPS1209011 Luas- km²Desa/kelurahan8 nagori Pamatang Silima Huta adalah sebuah kecamatan yang berada di Kabupaten Simalungun, Provinsi Sumatera Utara, Indonesia. Wilayah administratif Wilayah Kecamatan Pamatang Silima Huta terbagi m...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: The Principal's Office – news · newspapers · books · scholar · JSTOR (December 2023) (Learn how and when to remove this message) American TV series or program The Principal's OfficeGenreReality TVStarringJoey SussmanCountry of originUnited StatesNo. of seasons2No. of episodes21P...

American track athlete and football player (1934–2009) Glenn DavisPersonal informationFull nameGlenn Ashby Davis[1]NicknameJeepBorn(1934-09-12)September 12, 1934[1]Wellsburg, West Virginia, U.S.[1]DiedJanuary 28, 2009(2009-01-28) (aged 74)[1]Barberton, Ohio, U.S.[1]Height6 ft 0 in (183 cm)[1]Weight161 lb (73 kg)[1] Medal record Men's athletics Representing the United States Olympic Games 1956 Me...

Process of altering the timing of a valve lift event Cylinder head of Honda K20Z3. This engine uses continuously variable timing for the inlet valves Variable valve timing (VVT) is the process of altering the timing of a valve lift event in an internal combustion engine, and is often used to improve performance, fuel economy or emissions. It is increasingly being used in combination with variable valve lift systems. There are many ways in which this can be achieved, ranging from mechanical de...

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...
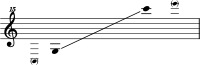
Mallet percussion instrument This article is about the musical instrument. For other uses, see Glockenspiel (disambiguation). GlockenspielA glockenspiel made by MalletechPercussion instrumentOther namesConcert bellsorchestral bellscarillonClassification Keyboard percussionHornbostel–Sachs classification111.222(Sets of percussion plaques)Playing range Related instruments Xylophonesong bellskeyboard glockenspiel Sound of a glockenspiel Problems playing this file? See media help. The glockensp...

L'Adoration de la Sainte Trinité par Albrecht Dürer (1511). La foi chrétienne (catholique, orthodoxe, protestante) est la croyance en la Trinité divine (Dieu unique en trois personnes : le Père, le Fils, le Saint-Esprit) et en la certitude de la rédemption des péchés apportée par la Passion et la Résurrection de Jésus. La foi est l’une des trois vertus théologales, avec l'espérance et la charité. Elle est exprimée de manière synthétique dans les différentes versions d...

Ben-HurMay McAvoy e Ramón Novarro in Ben-HurTitolo originaleBen-Hur: A Tale of the Christ Paese di produzioneStati Uniti d'America Anno1925 Durata143 min. Dati tecniciB/N e a colorirapporto: 1,33:1film muto Genereepico RegiaFred Niblo, Charles Brabin, Christy Cabanne, J.J. Cohn, Rex Ingram SoggettoLew Wallace SceneggiaturaJune Mathis, Carey Wilson, Bess Meredith, Katherine Hilliker, H.H. Caldwell ProduttoreIrving Thalberg Casa di produzioneMetro-Goldwyn-Mayer FotografiaClyde De Vinna, René ...

Parliamentary constituency in the United Kingdom, 1918 onwards Not to be confused with other constituencies listed at Monmouth constituency. MonmouthMynwyFormer County constituencyfor the House of CommonsBoundary of MonmouthMynwy in WalesPreserved countyGwentElectorate65,432 (December 2010)[1]Major settlementsAbergavenny, Chepstow, Monmouth1918–2024SeatsOneCreated fromMonmouth Boroughs, North Monmouthshire and South MonmouthshireReplaced byMonmouthshireTorfaenSeneddMonmouth, South W...

County in Michigan, United States This article needs to be updated. Please help update this article to reflect recent events or newly available information. (February 2021) County in MichiganLapeer CountyCountyLapeer County CourthouseLocation within the U.S. state of MichiganMichigan's location within the U.S.Coordinates: 43°05′N 83°13′W / 43.09°N 83.22°W / 43.09; -83.22Country United StatesState MichiganFoundedSeptember 18, 1822 (created)February 2, ...

College ice hockey team season 2022–23 Penn State Nittany Lions women's ice hockey seasonCHA regular season championCHA tournament champion ConferenceCollege Hockey AmericaHome icePegula Ice ArenaRankingsUSA Today#15USCHO.com#11RecordOverall27–8–2Conference12–1–1Home1–1–0Road1–1–0Neutral0–0–0Coaches and captainsHead coachJeff Kampersal (7th season)Assistant coachesAllison CoomeyMakenna NewkirkCaptain(s)Rene GangarosaMallory UihleinKiara ZanonPenn State Nittany Lions wom...

سيلان الهولندية نظام الحكم غير محدّد التاريخ التأسيس 1640 النهاية 1796 تعديل مصدري - تعديل كانت سيلان الهولندية (بالسنهالية: ලන්දේසි ලංකාව) محافظة تأسست فيما هو اليوم سريلانكا على يد شركة الهند الشرقية الهولندية. وكانت في الفترة من 1640 حتى 1796. على الرغم من أن ال�...

Untuk kegunaan lain, lihat Sandal (disambiguasi). Sandal wanita (sepatu sandal) dengan tumit tinggi Sandal jepit sandal Sendal yang biasa dipakai untuk mendaki gunung Sandal adalah salah satu model alas kaki yang terbuka pada bagian jari kaki atau tumit pemakainya. Bagian alas (sol) dihubungkan dengan tali atau sabuk yang berfungsi sebagai penjepit (penahan) di bagian jari, punggung kaki, ataupun pergelangan kaki agar sandal tidak terlepas dari kaki pemakainya. Sandal yang memiliki penutup di...

Эта статья — о материке. О регионе см. Северная Америка (регион). Северная Америка Северная Америка Территория24 365 000[1][2][3] км² Население579 000 000 (2016) чел. Плотность22,9 чел./км² Названия жителейсевероамериканец, американец Включает23 �...

Database of protein families For the Malaysian football labor union that used the acronym PFAM, see Professional Footballers Association of Malaysia. PfamContentDescriptionThe Pfam database provides alignments and hidden Markov models for protein domains.Data typescapturedProtein familiesOrganismsallContactResearch centerEBIPrimary citationPMID 19920124AccessData formatStockholm formatWebsitewww.ebi.ac.uk/interpro/entry/pfam/#tableDownload URLFTPMiscellaneousLicenseGNU Lesser General Pub...

Voce principale: Unione Sportiva Antonio Toma Maglie. U.S. A. Toma MaglieStagione 1953-1954Sport calcio Squadra Toma Maglie Allenatore Dino Bovoli Presidente Catalano Serie C15º Maggiori presenzeCampionato: Giorgino (33) Cappello (33) Miglior marcatoreCampionato: Veglianetti (17) 1952-53 1954-55 Si invita a seguire il modello di voce Questa voce raccoglie le informazioni riguardanti l'Unione Sportiva Antonio Toma Maglie nelle competizioni ufficiali della stagione 1953-1954. Indice 1 Or...
















































