تاريخ نظرية الحقل الكمومي
|
Read other articles:

Neue SynagogeNeue Synagoge, Oranienburger Strasse, Berlin-MitteAgamaAfiliasiYudaisme KonservatifRitusAshkenazKepemimpinanGesa EderbergDiberkati1866StatusAktifLokasiLokasiOranienburger Straße 29-31, Berlin, JermanKoordinat52°31′29″N 13°23′40″E / 52.52472°N 13.39444°E / 52.52472; 13.39444ArsitekturTipeSinagogeGaya arsitekturKebangkitan MoorPeletakan batu pertama1859Rampung1866SpesifikasiKapasitas3200 kursiKubah3Situs webwww.or-synagogue.de (sinagoge) [1] (mu...

Grand Prix Brasil 2012 Lomba ke-20 dari 20 dalam Formula Satu musim 2012 Detail perlombaan[1]Tanggal 25 November 2012Nama resmi Formula 1 Grande Prêmio Petrobras do Brasil 2012Lokasi Autódromo José Carlos Pace, São Paulo, BrasilSirkuit Fasilitas balapan permanenPanjang sirkuit 4.309 km (2.677 mi)Jarak tempuh 71 putaran, 305.909 km (190.083 mi)Cuaca Perlombaan dimulai: rintik-rintik hujan, hujan rintik-rintik semakin deras di akhir.[2] Temp Udara 19 °C (66 °F)&...
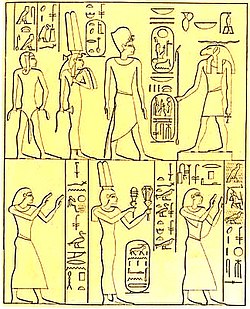
BintanathPermaisuri MesirIstri Kerajaan AgungNyonya Dua TanahNyonya Mesir Hulu dan Hilir, dll.BintanathPemakamanmakam QV71, Lembah Para Ratu, ThebesAyahRamses IIIbuIsetnofretPasanganRamses IIMerenptah? (dugaan)AnakSeorang putri yang namanya tidak diketahuiAgamaagama Mesir Kuno Bintanath Era: Kerajaan Baru(1550–1069 BC) Hieroglif Mesir Bintanath (atau Bentanath) merupakan putri kelahiran pertama dan kemudian Istri Kerajaan Agung Firaun Mesir, Ramses II.[1] Keluarga Bintanath kem...

Sampul CIA World Factbook 2016-2017 (edisi pemerintah) Edisi daring dari CIA World Factbook pada bulan Februari 2007 CIA World Factbook (ISSN 1553-8133) adalah publikasi tahunan dari Central Intelligence Agency (CIA), badan intelijen Amerika Serikat. CIA World Factbook berisi data-data almanak mengenai negara-negara di dunia. Di dalamnya terdapat ringkasan 2-3 halaman tentang masalah demografi, geografi, komunikasi, pemerintahan, ekonomi dan militer dari masing-masing 268 negara atau dependen...

Islam menurut negara Afrika Aljazair Angola Benin Botswana Burkina Faso Burundi Kamerun Tanjung Verde Republik Afrika Tengah Chad Komoro Republik Demokratik Kongo Republik Kongo Djibouti Mesir Guinea Khatulistiwa Eritrea Eswatini Etiopia Gabon Gambia Ghana Guinea Guinea-Bissau Pantai Gading Kenya Lesotho Liberia Libya Madagaskar Malawi Mali Mauritania Mauritius Maroko Mozambik Namibia Niger Nigeria Rwanda Sao Tome dan Principe Senegal Seychelles Sierra Leone Somalia Somaliland Afrika Selatan ...

Military rank of the United States For other countries that use this rank, see Colonel. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Colonel United States – news · newspapers · books · scholar · JSTOR (December 2022) (Learn how and when to remove this template message) ColonelColonel insignia. Style ...

Military Parks of the United States Vicksburg National Military Park, Illinois Memorial Kennesaw Mountain National Battlefield Park National Military Park, National Battlefield, National Battlefield Park, and National Battlefield Site are four designations for 25 battle sites preserved by the United States federal government because of their national importance. The designation applies to sites where historic battles were fought on American soil during the armed conflicts that shaped the grow...

Japanese corporation Not to be confused with Mitsui Group. Mitsui & Co., Ltd. 三井物産株式会社Headquarters in Ōtemachi, Chiyoda, TokyoCompany typePublic (KK)Traded asTYO: 8031TOPIX Core 30 ComponentIndustryTrading CompaniesFoundedJuly 25, 1947; 76 years ago (1947-07-25)FounderTakashi Masuda, Tatsuzo MinakamiHeadquarters2-1, Otemachi 1-chome, Chiyoda-ku, Tokyo 100-8631, Japan, Tokyo, JapanArea served132 Offices in 64 Countries / Regions (2020)Key peopleTatsuo Yas...

Disambiguazione – Se stai cercando l'ingegnere americano, amministratore della NASA, vedi Thomas O. Paine. (EN) «My country is the world… and my religion is to do good.» (IT) «La mia nazione è il mondo… e la mia religione è fare il bene.» (T. Paine) Ritratto di Thomas Paine di Laurent Dabos Thomas Paine (Thetford, 29 gennaio 1737 – New York, 8 giugno 1809) è stato un rivoluzionario, politico, intellettuale, filosofo illuminista e studioso britannico, considerato uno dei Padri ...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

密西西比州 哥伦布城市綽號:Possum Town哥伦布位于密西西比州的位置坐标:33°30′06″N 88°24′54″W / 33.501666666667°N 88.415°W / 33.501666666667; -88.415国家 美國州密西西比州县朗兹县始建于1821年政府 • 市长罗伯特·史密斯 (民主党)面积 • 总计22.3 平方英里(57.8 平方公里) • 陸地21.4 平方英里(55.5 平方公里) • ...

Overview of the transportation in the Philippines The MRT Line 3 in 2024 Transportation in the Philippines covers the transportation methods within this archipelagic nation of over 7,500 islands. From a previously underdeveloped state of transportation, the government of the Philippines has been improving transportation through various direct infrastructure projects, and these include an increase in air, sea, road, and rail transportation and transport hubs.[1] Jeepneys are a popular ...

American diplomat (born 1958) Stephen MullUnder Secretary of State for Political AffairsActingIn officeJune 5, 2018 – August 29, 2018PresidentDonald TrumpPreceded byTom ShannonSucceeded byDavid HaleCoordinator for Iran Nuclear ImplementationIn officeSeptember 25, 2015 – August 2017PresidentBarack ObamaDonald TrumpPreceded byJoseph Macmanus (Acting)Succeeded byBrian Hook (Special Representative for Iran)United States Ambassador to PolandIn officeNovember 8, 2012 –&...

Dumfries, Lochmaben and Lockerbie RailwayOverviewStatusabsorbed by Caledonian RailwayLocaleScotlandHistoryOpened1 September 1863Closed18 April 1966TechnicalTrack gauge1,435 mm (4 ft 8+1⁄2 in) Route map Legend Caledonian Main Line Lockerbie Lochmaben Shieldhill Amisfield Locharbriggs Glasgow, Dumfries & Carlisle Rly Castle Douglas & Dumfries Rly Dumfries Goods (CR) Dumfries (G&SWR) Dumfries Goods (G&SWR) Glasgow, Dumfries & Carlisle Rly This...

International athletics championship event2021 European Athletics Indoor ChampionshipsDates4–7 MarchHost cityToruń, PolandVenueArena ToruńLevelSeniorTypeIndoorEvents26Participation659 athletes from 46 nations← Glasgow 2019 Istanbul 2023 → The 2021 European Athletics Indoor Championships was held from 4 to 7 March 2021 at the Arena Toruń in Toruń, Poland.[1] This was the second time this event was held in Poland after the 1975 edition in Katowice. The four-day compet...

Peta Rouvres-la-Chétive. Rouvres-la-Chétive merupakan sebuah komune di departemen Vosges yang terletak pada sebelah timur laut Prancis. Lihat pula Komune di departemen Vosges Referensi INSEE lbsKomune di departemen Vosges Les Ableuvenettes Ahéville Aingeville Ainvelle Allarmont Ambacourt Ameuvelle Anglemont Anould Aouze Arches Archettes Aroffe Arrentès-de-Corcieux Attignéville Attigny Aulnois Aumontzey Autigny-la-Tour Autreville Autrey Auzainvilliers Avillers Avrainville Avranville Aydoi...

العلاقات الباهاماسية الفنلندية باهاماس فنلندا باهاماس فنلندا تعديل مصدري - تعديل العلاقات الباهاماسية الفنلندية هي العلاقات الثنائية التي تجمع بين باهاماس وفنلندا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه ا...

Religious garment worn in Japan A kannushi (right) wearing a jōe Jōe (浄衣, sometimes translated as pure cloth) is a garment worn in Japan by people attending religious ceremonies and activities, including Buddhist and Shinto related occasions. The jōe is essentially a white kariginu, traditional hunting robes worn by nobles during the Heian period. Though both Shinto and Buddhist priests wear jōe to rituals, laymen also occasionally wear the jōe, such as when participating in pilgrima...

Philippine government agency responsible for Metro Manila region Law enforcement agency Metropolitan Manila Development AuthorityPangasiwaan sa Pagpapaunlad ng Kalakhang Maynila (Filipino)AbbreviationMMDAMottoMarangal, Matapat, Disiplinado Ako[I am] Honorable, Honest, and DisciplinedAgency overviewFormedNovember 5, 1975; 48 years ago (1975-11-05)Annual budget₱4.78 billion (2020)[1]Jurisdictional structureOperations jurisdictionPhilippinesLegal jurisdictionMetr...
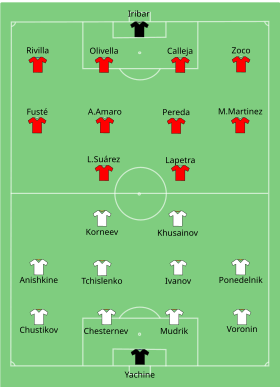
Espagne - URSS Contexte Compétition Euro 1964 Date 21 juin 1964 Stade Stade Santiago Bernabéu Lieu Madrid, Espagne Affluence 79 115 spectateurs Résultat Espagne 2-1 Union soviétique Mi-temps 1-1 0 Navigation Finale de 1960 Finale de 1968 modifier La finale du championnat d'Europe de football 1964 voit s'affronter l'équipe d'Espagne contre celle d'URSS, championne d'Europe en titre. Le pays hôte espagnol remporte sa première compétition internationale lors de la deuxième �...
