برج هانوي
|
Read other articles:

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Taiwan – berita · surat kabar · buku · cendekiawan · JSTOR Republik Tiongkok beralih ke halaman ini. Untuk Republik Rakyat Tiongkok, lihat Tiongkok. Untuk kegunaan lain, lihat Republik Tiongkok (disambiguasi)...

Mexican politician In this Spanish name, the first or paternal surname is Sáenz and the second or maternal family name is Garza. Aarón Sáenz Garza in 1922 Aarón Sáenz Garza (1 June 1891 – 26 February 1983) was a Mexican politician.[1] Biography He was born in Monterrey, Nuevo León. Sáenz Garza served as Secretary of Foreign Affairs during Calles' time as president. During his tenure, he continuously defended the Calles Administration's decision to cut oil to the U...

Ini adalah sebuah nama Islandia. Nama terakhirnya adalah sebuah nama keluarga, namun tokoh ini biasa disebut dengan nama panggilannya, Baltasar. Baltasar KormákurBaltasar Kormákur di FFIKV ke-42, 2007LahirBaltasar Kormákur Samper27 Februari 1966 (umur 58)Reykjavík, IslandiaPekerjaanAktor, sutradara, produserTahun aktif1992–sekarang Baltasar Kormákur Samper (kelahiran 27 Februari 1966) adalah seorang aktor, sutradara film dan teater Islandia. Ia dikenal secara profesional seba...

Railway station in Ontario, Canada BramptonGeneral informationLocation27/31 Church Street WestBrampton, OntarioCanadaCoordinates43°41′13″N 79°45′53″W / 43.68694°N 79.76472°W / 43.68694; -79.76472Owned byMetrolinx (station) Canadian National Railway (tracks)Platforms2 side platformsTracks2Connections Downtown Brampton TerminalConstructionStructure typeUnstaffed stationParking962 spacesAccessibleYesOther informationStation codeGO Transit: BRFare zone33His...

Reruntuhan Monolit Silwan, makam dari periode Bait Suci Pertama. Nekropolis Silwan (Inggris: Silwan necropolis) adalah tempat pemakaman kuno paling penting di Israel, dan diyakini digunakan oleh para pejabat tinggi yang pernah tinggal di Yerusalem. Makam-makam itu digali antara abad ke-9 dan abad ke-7 SM[1] Terletak di lereng timur berbatu karang pada Lembah Kidron, menghadap ke arah bagian tertua Yerusalem. Desa orang Arab, Silwan, dibangun di kemudian hari di atas nekropolis ter...

Indian locomotive class WAG–6VSKP based WAG-6C locos at Koraput.Type and originPower typeElectricDesignerHitachiBuilderHitachiOrder number85/RSF/459/1/(LT-33)Build date1988Total produced WAG-6B:6 WAG-6C:6 SpecificationsConfiguration: • UIC WAG-6B:Bo'Bo'Bo' WAG-6C:Co'Co • Commonwealth WAG-6B:Bo-Bo-Bo WAG-6C:Co-Co Gauge5 ft 6 in (1,676 mm)Bogies2 axle double stage field excitationWheel diameterNew: 1,140 mm (3 ft 9 in)Half-w...

Early phase of the mid-7th-century Arab conquest of Iran Arab conquest of ParsPart of Islamic conquest of PersiaRuins of a Zoroastrian temple in BishapurDate638/9–650/1LocationParsResult Rashidun victoryBelligerents Sasanian Empire Rashidun CaliphateCommanders and leaders Yazdegerd IIIShahrag †Mahak Uthman ibn Abi al-As al-ThaqafiAl-Ala'a Al-HadramiAl-Jarud ibn Mu'alla †Al-Sawwar ibn Hammam †Khulayd ibn al-Mundhir ibn Sawa'Ubayd Allah ibn Ma'mar &...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

Sailing at the Olympics Sailingat the Games of the XXVII OlympiadRushcutters Bay.VenuesSydneyDatesFirst race: 17 September 2000 (2000-09-17)Last race: 30 September 2000 (2000-09-30)Competitors402 (307 men, 95 women)← 19962004 → Sailing at the2000 Summer OlympicsMistralmenwomenEuropewomenLaseropenFinnmen470menwomen49eropenTornadoopenStaropenSolingopenvte Sailing at the 2000 Summer Olympics in Sydney was held from 17 to 30 September 2000 at th...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

Core city in Honshu, Japan Core city in Honshu, JapanWakayama 和歌山市Core cityWakayama CityWakayama Castle, Nishinomaru Garden, Saikazaki, Kimiidera Temple, Downtown Wakayama viewed from the castle keep FlagSealLocation of Wakayama in Wakayama PrefectureWakayamaCoordinates: 34°14′N 135°10′E / 34.233°N 135.167°E / 34.233; 135.167CountryJapanRegionHonshu (Kansai)PrefectureWakayamaGovernment • MayorMasahiro ObanaArea • Total208.84 ...
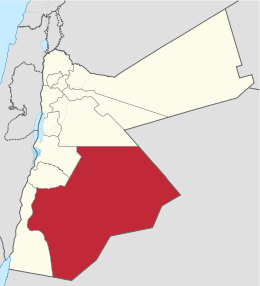
يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) محافظة معان. تتناول هذه القائمة المواقع الأثرية المسجَّلة رسمياً لدى دائرة الآثار العامة التابعة لوزارة...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要編修,以確保文法、用詞、语气、格式、標點等使用恰当。 (2013年8月6日)請按照校對指引,幫助编辑這個條目。(幫助、討論) 此條目剧情、虛構用語或人物介紹过长过细,需清理无关故事主轴的细节、用語和角色介紹。 (2020年10月6日)劇情、用語和人物介紹都只是用於了解故事主軸,輔助�...

الحديقة العامة {{{تعليق_بديل}}}المدخل الرئيسي للحديقة العامة تاريخ الافتتاح 1949 الموقع حي محطة بغداد، حلب, سوريا البلد سوريا الإحداثيات 36°12′35″N 37°08′50″E / 36.20972°N 37.14722°E / 36.20972; 37.14722 مساحة الأرض 17 هكتاراً المالك مجلس مدينة حلب تعديل مصدري - تعديل تعدّ «ال...

Citrus fruit and plant Naartjie redirects here. For other uses, see Naartjie (clothing retailer). Mikan redirects here. For the basketball player, see George Mikan. For other uses, see Mikan (disambiguation). Citrus unshiu Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Eudicots Clade: Rosids Order: Sapindales Family: Rutaceae Genus: Citrus Species: C. unshiu Binomial name Citrus unshiu(Yu.Tanaka ex Swingle) Marcow. Citrus unshiu is a semi-seedle...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (April 2018) (Learn how and when to remove this message) This article relies largely or entirely on a single source. Relevant...

Features from accelerated segment test (FAST) is a corner detection method, which could be used to extract feature points and later used to track and map objects in many computer vision tasks. The FAST corner detector was originally developed by Edward Rosten and Tom Drummond, and was published in 2006.[1] The most promising advantage of the FAST corner detector is its computational efficiency. Referring to its name, it is indeed faster than many other well-known feature extraction me...
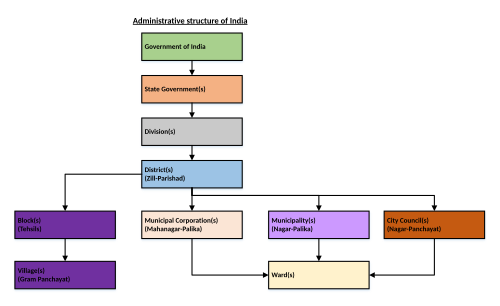
Administrative division of some South Asian countries For the Australian rural subdivision, see Block (rural Australia). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Block district subdivision – news · newspapers · books · scholar · JSTOR (November 2016) (Learn how and when to remove this message) A ...

جمهورية هولندا جمهورية هولنداعلم جمهورية هولنداشعار عاصمة لاهاي نظام الحكم غير محدّد نظام الحكم جمهورية اللغة الرسمية الهولندية التاريخ التأسيس 26 يوليو 1581 النهاية 19 يناير 1795 السكان السكان 1880500 (1795) العملة دالر إمبراطوري هولنديخولده هولندي تعدي...



