Uji hipotesis
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2022. Cotinusa dimidiata Klasifikasi ilmiah Kerajaan: Animalia Filum: Arthropoda Kelas: Arachnida Ordo: Araneae Famili: Salticidae Genus: Cotinusa Spesies: Cotinusa dimidiata Nama binomial Cotinusa dimidiataSimon, 1900 Cotinusa dimidiata adalah spesies laba...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Project Pop – berita · surat kabar · buku · cendekiawan · JSTOR Project PopAsalBandung, IndonesiaGenreHumor pop Hip Hop R&BTahun aktifJuni 1996–sekarangLabelMusica Studio'sRPMHalo EntertainmentAngg...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

Mechanical engineer Margaret IngelsBorn(1892-10-25)October 25, 1892Paris, KentuckyDiedDecember 13, 1971(1971-12-13) (aged 79)Lexington, KentuckyEducationB.S. in Mechanical Engineering, 1916Alma materUniversity of KentuckyOccupationMechanical EngineeringEmployerCarrier-Lyle CorporationKnown forPioneer in the development of air conditioning. First female engineering graduate from the University of Kentucky; second woman engineering graduate in the United States; first woman to re...

Radio station in Raleigh, North CarolinaWKIX-FMRaleigh, North CarolinaBroadcast areaRaleigh–DurhamResearch TriangleFrequency102.9 MHzBrandingKIX 102ProgrammingFormatClassic hitsOwnershipOwnerCurtis Media Group(FM 102.9 LLC)Sister stationsWBBB, WKJO, WKIX, WKXU, WPLW-FM, WPTF, WQDR, WQDR-FMHistoryFirst air dateJuly 1, 1998 (1998-07-01) (as WWND)Former call signsWWND (1998–2001)WWMY (2001–2010)[1]Call sign meaningKix (branding)Technical information[2]Licensi...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

Chronologies Chronologie du sport 2002 2003 2004 2005 2006 2007 2008Mois :Jan - Fév - Mar - Avr - Mai - Juin Juil - Aoû - Sep - Oct - Nov - Déc 2004 ◄◄ 2005 en sport ►► 2006 Chronologie dans le monde 2002 2003 2004 2005 2006 2007 2008Décennies :1970 1980 1990 2000 2010 2020 2030Siècles :XIXe XXe XXIe XXIIe XXIIIeMillénaires :Ier IIe IIIe Chronologies géographiques Afrique Afrique du Sud, Algérie, ...

la Mâtre la Rivière Mâtre sous la neige près de Messimy-sur-Saône la Mâtre sur OpenStreetMap. Caractéristiques Longueur 10,6 km [1] Bassin collecteur Rhône Débit moyen (Messimy-sur-Saône) Nombre de Strahler 2 Organisme gestionnaire SIAH[2] Régime pluvial océanique Cours Source près du lieu-dit le Vernay · Localisation Villeneuve · Altitude 275 m · Coordonnées 46° 01′ 24″ N, 4° 50′ 12″ E Confluence la Saône · Localisation Me...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...
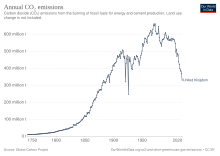
Emissions, impacts and responses of the United Kingdom related to climate change Central England temperature dataset showing a warming trend in the UK between 1659 and 2014. Climate change is impacting the environment and human population of the United Kingdom (UK). The country's climate is becoming warmer, with drier summers and wetter winters. The frequency and intensity of storms, floods, droughts and heatwaves is increasing, and sea level rise is impacting coastal areas. The UK is also a ...

Fabio LeimerFabio Leimer sulla Racing Engineering in gara 1 di GP2 del Belgio 2013Nazionalità Svizzera Automobilismo CategoriaGP2 SquadraRacing Engineering Modifica dati su Wikidata · Manuale Fabio Leimer (Rothrist, 17 aprile 1989) è un pilota automobilistico svizzero. Indice 1 Carriera 1.1 Karting 1.2 Formula BMW 1.3 Formula Renault 1.4 International Formula Master 1.5 GP2 Series 1.6 Formula 1 2 Risultati 2.1 Sommario 2.2 Risultati in GP2 Series 2.3 Risultati in GP2 Asia ...

Comic book series featuring the DC Comics heroes of the same name Green LanternCover of Green Lantern #1 (fall 1941) by Howard Purcell[1]Publication informationPublisherDC ComicsSchedule List (Vol. 1)Quarterly: #1–18Bimonthly: #19–38(Vol. 2)Bimonthly: #1–9; #82–96Eight times a year: #10–81Monthly: #97–224(Vol. 3)Monthly: #1–181(Vol. 4)Monthly: #1–67(Vol. 5)Monthly: #1–52(Green Lanterns)Twice Monthly: #1–57(Hal Jordan and the Green Lantern Corps)Twice Monthly: #1–...

بطولة أمم إفريقيا للمحليين 20112011 Championnat d'Afrique des Nations (بالفرنسية)تفاصيل المسابقةالبلد المضيف السودانالتواريخ4 حتى 25 فبراير 2011الفرق16الأماكن5المراكز النهائيةالبطل تونسالوصيف أنغولاالمركز الثالث السودانالمركز الرابع الجزائرإحصائيات المسابقةالمباريات المل...

جائحة فيروس كورونا في الجمهورية العربية الصحراوية الديمقراطية 2020 المرض مرض فيروس كورونا 2019 السلالة فيروس كورونا المرتبط بالمتلازمة التنفسية الحادة الشديدة النوع 2 التواريخ 25 يوليو 2020 المكان الجمهورية العربية الصحراوية الديمقراطية تعديل مصدري - تعديل جزء من سلسلة ...

Tax deduction Part of a series onTaxation An aspect of fiscal policy Policies Government revenue Property tax equalization Tax revenue Non-tax revenue Tax law Tax bracket Flat tax Tax threshold Exemption Credit Deduction Tax shift Tax cut Tax holiday Tax amnesty Tax advantage Tax incentive Tax reform Tax harmonization Tax competition Tax withholding Double taxation Representation Unions Medical savings account Economics General Theory Price effect Excess burden Tax incidence Laffer curve Opti...

Christian scholar, ascetic, and theologian (c. 185 – c. 253) This article is about the third-century Christian scholar. For the pagan philosopher with the same name, see Origen the Pagan. For other uses, see Origen (disambiguation). Not to be confused with Orogen. OrigenRepresentation of Origen writing, from a manuscript of In numeros homilia XXVII, c. 1160Bornc. 185 ADAlexandria, Province of Egypt, Roman EmpireDiedc. 253 AD (aged c. 69)Probably Tyre, Phoenice, Roman EmpireAlma materCa...

American animated showcase series Not to be confused with The Wacky World of Tex Avery. The Tex Avery ShowTitle card seen at the end of the show introCountry of originUnited StatesOriginal languageEnglishNo. of episodes99ProductionRunning time22 minutesOriginal releaseNetworkCartoon NetworkReleaseNovember 1, 1996 (1996-11-01)[1] –June 15, 2002 (2002-06-15) The Tex Avery Show is an American animated showcase series of Metro-Goldwyn-Mayer and Warner Bros. cartoon shorts...

2006 video by Amon AmarthWrath of the NorsemenVideo by Amon AmarthReleased12 May 2006 (2006-05-12)GenreMelodic death metalLength443:46LabelMetal Blade Professional ratingsReview scoresSourceRatingMetal-Rules[1] Wrath of the Norsemen is a live DVD by Swedish melodic death metal band Amon Amarth. It features live footage of the band playing their music. It also contains interviews and behind-the-scenes footage. The DVD was certified gold by the RIAA. Track listin...

Station of the Berlin U-Bahn Reinickendorfer StraßePlatform view of Reinickendorfer StraßeGeneral informationLocationMitteOwned byBerliner VerkehrsbetriebeOperated byBerliner VerkehrsbetriebePlatforms1 island platformTracks2Train operatorsBerliner VerkehrsbetriebeConnectionsConstructionStructure typeUndergroundOther informationFare zoneVBB: Berlin A/5555[1]HistoryOpened8 March 1923; 101 years ago (1923-03-08)Services Preceding station Berlin U-Bahn Following statio...

Pour les articles homonymes, voir Défenseur et Arrière. Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (novembre 2018). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références »...



















































