Read other articles:

Grigori N. VoitinskyГригорий Наумович Войтинский Kepala Biro Timur JauhPerdana MenteriVladimir Lenin Informasi pribadiLahirGrigori Zarkhin17 April 1893NevelMeninggal11 Juni 1953MoskowPartai politikPartai Komunis Uni Soviet (CPSU)Sunting kotak info • L • B Grigori Naumovich Voitinsky, lahir Zarkhin (Rusia: Григорий Наумович Войтинскийcode: ru is deprecated ; 1893-1953) adalah seorang pejabat resmi dari Komintern Bolshevik. Dia d...

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Siemens & Halske – berita · surat kabar · buku · cendekiawan · JSTOR (Desember 2013) Siemens & HalskeIndustriTeknik listrikNasibBergabung dengan SiemensDidirikan1847PendiriWerner von SiemensJohann Geo...

Austronesian language spoken in the Philippines Not to be confused with Melanau language. This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs editing to comply with Wikipedia's Manual of Style. Please help improve the content. (April 2021) (Learn how and when to remove this template message) This article may overuse or misuse color, making it hard to understand for color-bl...

Pour les articles homonymes, voir Fort Royal. Fort-de-France Vue de Cathédrale Saint-Louis à l'arrivée des bateaux en provenance des Trois-Îlets, le centre d'affaire Pointe Simon, le Fort Saint-Louis, centre ville et le Jardin de Balata. Blason Logo Administration Pays France Région Martinique Département Martinique Arrondissement Fort-de-France (chef-lieu) Intercommunalité Communauté d'agglomération du Centre de la Martinique(siège) Maire Mandat Didier Laguerre (PPM) 2020-2026 Cod...

Bupati KediriLambang Kabupaten KediriPetahanaHanindhito Himawan Pramanasejak 26 Februari 2021KediamanPendapa Kabupaten KediriMasa jabatan5 tahunDibentuk1800; 223 tahun lalu (1800)Pejabat pertamaPangeran Slamet PoerbonegoroSitus webkedirikab.go.id Berikut ini adalah Daftar Bupati Kabupaten Kediri dari masa ke masa.[1] No Bupati Mulai Jabatan Akhir Jabatan Prd. Ket. Wakil Bupati 1 Pangeran Slamet Poerbonegoro 1800 1825 1 2 Tjakraningrat Teposono 1825 1850 2 3 Djojonegoro 1850 ...

Lubang sembur lumba-lumba hidung botol. Dalam biologi, lubang sembur adalah lubang di atas kepala Cetacea tempat binatang bernapas. Lubang sembur homologus dengan nostril mamalia lainnya. Ketika paus mencapai permukaan perairan untuk bernapas, mereka akan mengeluarkan air melalui lubang sembur. Pengeluaran ini, diketahui sebagai sembur, dapat terlihat dari jauh. Pengawasan otoritas Microsoft Academic Artikel bertopik hewan ini adalah sebuah rintisan. Anda dapat membantu Wikipedia dengan menge...

Kobayashi Kana小林香菜Kobayashi Kana di Japan Expo 2009Informasi latar belakangNama lahirKobayashi Kana (小林香菜code: ja is deprecated )Nama lainKK, Kaachi (かぁちcode: ja is deprecated ),Kacchan (かっちゃんcode: ja is deprecated )Lahir17 Mei 1991 (umur 32)Asal Tokyo, JepangGenreJ-popPekerjaanPenyanyiTahun aktif2006–kiniLabelDefSTAR RecordsArtis terkaitAKB48 2006 - 2016 Kana Kobayashi (小林香菜code: ja is deprecated , Kobayashi Kana, lahir 17 Mei 1991) atau akrab d...

Candi Mendut Candi Mendut (bahasa Jawa: ꦕꦟ꧀ꦝꦶꦩꦼꦤ꧀ꦢꦸꦠ꧀, translit. Candhi Mendut) adalah sebuah candi bercorak Buddha. Candi yang terletak di Desa Mendut, Jalan Mayor Kusen Kota Mungkid, Kabupaten Magelang, Jawa Tengah ini, letaknya berada sekitar 3 kilometer dari Candi Borobudur.7°36′17.17″S 110°13′48.01″E / 7.6047694°S 110.2300028°E / -7.6047694; 110.2300028 Masa pembuatan Reruntuhan candi Mendut sebelum dipugar, tahun 188...

Parliamentary elections in Albania Politics of Albania Constitution Human rights Executive President: Bajram Begaj (list) Prime Minister: Edi Rama (list) Deputy Prime Minister: Belinda Balluku (list) Cabinet Legislature Parliament Speaker: Lindita Nikolla (list) Committees Members Leader of the Opposition Judiciary Constitutional Court Administrative Court Court of Justice (ordinary jurisdiction) Supreme Court Administrative divisions Counties Municipalities CitiesVillages Elections Recent el...

Cet article est une ébauche concernant le droit. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Un dépôt de mendicité était un établissement de « réclusion des mendiants et gens sans-aveu ». La mendicité était considérée, dans l'Ancien Droit et jusque dans le code pénal français de 1810, comme un délit. Les dépôts de mendicité accueillaient une population hétéroclite de marginaux ...

У Вікіпедії є статті про інші значення цього терміна: Новосілка. село Новосілка Церква святого архистратига МихаїлаЦерква святого архистратига Михаїла Країна Україна Область Тернопільська область Район Чортківський район Громада Заліщицька міська громада Код КАТ�...

Perang Makedonia PertamaBagian dari Peperangan Makedonia/Perang Punisia KeduaMediterania tahun 218 SMTanggal214–205 SMLokasiMakedonia dan IliriaHasil Buntu; Perdamaian PhoenicePihak terlibat Republik RomawiKerajaan IliriaLiga AitoliaKerajaan PergamonKerajaan SpartaElisMessenia MakedoniaLiga AkhaiaTokoh dan pemimpin Marcus Valerius LaevinusScerdilaidasAttalus IMachanidas † Filipus V dari MakedoniaPhilopoemen Perang Makedonia Pertama (214–205 SM) adalah perang yang terjadi antara Rom...

Large open-air venue used for public events in the ancient Roman Empire The site of the former Circus Maximus in modern-day Rome 'Circus (building)' redirects here. For the British English use of circus to describe circular housing projects, see crescent (architecture). A Roman circus (from the Latin word that means circle) was a large open-air venue used mainly for chariot races, although sometimes serving other purposes. It was similar to the ancient Greek hippodrome. Along with theatres an...

Football league seasonLiga Primera de NicaraguaSeason2019–20ChampionsApertura:Real EstelíClausura:Real EstelíRelegatedDeportivo Las SabanasCONCACAF LeagueReal Estelí ManaguaMatches played196Goals scored459 (2.34 per match)Top goalscorerApertura: Carlos Félix(10 goals) Clausura: Fernando Villalpando(10 goals)Biggest home winApertura: Managua 5–0 Real Madriz(26 October 2019) Clausura: Walter Ferretti 7–0 Chinandega(29 March 2020)Biggest away winApertura: Chinandega 1–4 Real Est...

Australian federal by-election 1984 Corangamite by-election 18 February 1984 First party Second party Third party Candidate Stewart McArthur Gavan O'Connor David Seymour Party Liberal Labor National Popular vote 32,083 25,517 9,794 Percentage 46.7% 37.1% 14.2% Swing 11.5 4.7 14.2 TPP 59.4% 40.6% TPP swing 1.2 1.2 MP before election Tony Street Liberal Elected MP Stewart McArthur Liberal A by-election was held for the Australian House of Representatives seat of Corangamite o...

神代 明ペンネーム 神代 明(かみしろ あきら)誕生 (1971-02-10) 1971年2月10日(53歳)大阪府職業 ライトノベル作家活動期間 2001年 -代表作 『プリズム☆ハーツ!!』シリーズ主な受賞歴 第1回スーパーダッシュ小説新人賞大賞デビュー作 『世界征服物語 〜ユマの大冒険〜』 ウィキポータル 文学テンプレートを表示 神代 明(かみしろ あきら、1971年2月10日 - )は、日本の小�...

British adventurer and travel writer (1907–1971) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Peter Fleming writer – news · newspapers · books · scholar · JSTOR (July 2013) (Learn how and when to remove this message) Peter FlemingOBE DLBornRobert Peter Fleming(1907-05-31)31 May 1907Mayfair, Lon...

В Википедии есть статьи о других людях с такой фамилией, см. Пивненко. Валентина Николаевна Пивненко 20 ноября 2015 3-й председатель Комитета по проблемам Севера и Дальнего Востока Государственной Думы 19 января 2000 года — 21 декабря 2011 года Предшественник Борис Григорьевич...
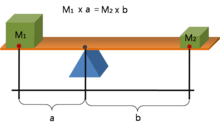
Product of a distance and physical quantity Not to be confused with Momentum. For the mathematical concept, see Moment (mathematics). For the moment of a force, sometimes shortened to moment, see Torque. Part of a series onClassical mechanics F = d p d t {\displaystyle {\textbf {F}}={\frac {d\mathbf {p} }{dt}}} Second law of motion History Timeline Textbooks Branches Applied Celestial Continuum Dynamics Kinematics Kinetics Statics Statistical mechanics Fundamentals Acceleration Angular moment...

This article may be in need of reorganization to comply with Wikipedia's layout guidelines. Please help by editing the article to make improvements to the overall structure. (November 2021) (Learn how and when to remove this message) Part of a series onTaxation An aspect of fiscal policy Policies Government revenue Property tax equalization Tax revenue Non-tax revenue Tax law Tax bracket Flat tax Tax threshold Exemption Credit Deduction Tax shift Tax cut Tax holiday Tax amnesty Tax advantage...