Read other articles:

Jawa Tengah IVDaerah Pemilihan / Daerah pemilihanuntuk Dewan Perwakilan RakyatRepublik IndonesiaWilayah Daftar Kabupaten : Karanganyar Sragen Wonogiri ProvinsiJawa TengahPopulasi3.013.632 (2023)[1]Elektorat2.313.625 (2024)[2]Daerah pemilihan saat iniDibentuk2004Kursi7Anggota  Luluk Nur Hamidah (PKB)  Bambang Wuryanto (PDI-P)  Agustina Wilujeng Pramestuti (PDI-P)  Paryono (PDI-P)  Dolfie Othniel Frederic Palit (PDI-P)  Endang Maria Astuti (Gol...

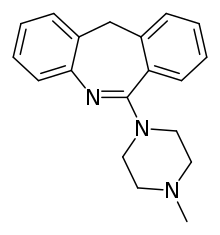
Sedative and hypnotic medication PerlapineClinical dataTrade namesHypnodine, PipnodineOther namesAW-14233; HF-2333; MP-11; PLP 100-127; 6-(4-Methyl-1-piperazinyl)morphanthridineIdentifiers IUPAC name 6-(4-Methylpiperazin-1-yl)-11H-benzo[c][1]benzazepine CAS Number1977-11-3PubChem CID16106ChemSpider15291UNII4N8UJJ27IMKEGGD01438ChEBICHEBI:31983ChEMBLChEMBL340801CompTox Dashboard (EPA)DTXSID1048758 ECHA InfoCard100.241.831 Chemical and physical dataFormulaC19H21N3Molar mass291.398 g·mol−...

Conway knotBraid no.3[1]Hyperbolic volume11.2191Conway notation.−(3,2).2[2]Thistlethwaite11n34Otherhyperbolic, prime, slice (topological only), chiral Conway knot emblem on a closed gate at Isaac Newton Institute. Conway knot Prime knot named for John Horton Conway In mathematics, in particular in knot theory, the Conway knot (or Conway's knot) is a particular knot with 11 crossings, named after John Horton Conway.[1] It is related by mutation to the Kino...

This article needs to be updated. Please help update this article to reflect recent events or newly available information. (September 2019) George Washington and Calvin Coolidge on the 1926 Sesquicentennial of American Independence commemorative half dollar Several presidents of the United States have appeared on currency. The president of the United States has appeared on official banknotes, coins for circulation, and commemorative coins in the United States, the Confederate States of Ameri...

Fiction genre depicting female same-sex relationships An example of yuri-inspired artwork. Works depicting intimate relationships between school classmates are common in the yuri genre. Yuri (Japanese: 百合, lit. lily), also known by the wasei-eigo construction girls' love (ガールズラブ, gāruzu rabu), is a genre of Japanese media focusing on intimate relationships between female characters. While lesbianism is a commonly associated theme, the genre is also inclusive of works depictin...

Trend in art and design Exotic figures in Jules Migonney's Venus mauresque Exoticism (from exotic) is a trend in art and design, whereby artists became fascinated with ideas and styles from distant regions and drew inspiration from them. This often involved surrounding foreign cultures with mystique and fantasy which owed more to the culture of the people doing the exoticism than to the exotic cultures themselves: this process of glamorisation and stereotyping is called exoticisation. History...

Extinct genus of dinosaurs SiamraptorTemporal range: Aptian~120–112 Ma PreꞒ Ꞓ O S D C P T J K Pg N Skeletal reconstruction and size comparison of Siamraptor suwati Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Clade: Dinosauria Clade: Saurischia Clade: Theropoda Clade: †Allosauria Clade: †Carcharodontosauria Genus: †SiamraptorChokchaloemwong et al., 2019 Species: †S. suwati Binomial name †Siamraptor suwatiChokchaloemwong et al...

Theorem about inclusions between Sobolev spaces In mathematics, there is in mathematical analysis a class of Sobolev inequalities, relating norms including those of Sobolev spaces. These are used to prove the Sobolev embedding theorem, giving inclusions between certain Sobolev spaces, and the Rellich–Kondrachov theorem showing that under slightly stronger conditions some Sobolev spaces are compactly embedded in others. They are named after Sergei Lvovich Sobolev. Sobolev embedding theorem G...

Kenjiro TsudaKenjiro Tsuda, 2018Nama asal津田 健次郎Lahir11 Juni 1971 (umur 52)[1] Prefektur Osaka, Jepang[1]AlmamaterUniversitas MeijiPekerjaan Pemeran pengisi suara narator sutradara Tahun aktif1995–sekarangAgenANDSTIRTinggi170 cm (5 ft 7 in)[1]Situs webtsudaken.jp Kenjiro Tsuda (津田 健次郎code: ja is deprecated , Tsuda Kenjirō, lahir 11 Juni 1971) adalah seorang pemeran, pengisi suara, narator, dan sutradara asal Prefektu...

Literary work This article is about the play. For the science fiction novel, see Footfall. For the film, see Footfalls (film). For other uses, see Footfall (disambiguation). Paperback Faber, 1976 First Edition Footfalls is a play by Samuel Beckett. It was written in English, between 2 March and December 1975 and was first performed at the Royal Court Theatre as part of the Samuel Beckett Festival, on May 20, 1976 directed by Beckett himself. Billie Whitelaw, for whom the piece had been writte...

Lega Pro Prima Divisione 2012-2013 Competizione Lega Pro Prima Divisione Sport Calcio Edizione 35ª Organizzatore Lega Italiana Calcio Professionistico Date dal 1º settembre 2012al 16 giugno 2013 Luogo  Italia Partecipanti 33 Formula 2 gironi all'italiana A/R, play-off e play-out Risultati Vincitore Trapani (1º titolo)Avellino (2º titolo) Promozioni TrapaniCarpiAvellinoLatina Retrocessioni (le squadre scritte in corsivo sono poi state ripescate)TrevisoPortogruaroCuneoAndria B...

2021 Tasmanian state election ← 2018 1 May 2021 2024 → All 25 seats in the House of Assembly13 seats needed for a majorityOpinion pollsRegistered394,432   First party Second party Third party   Leader Peter Gutwein Rebecca White Cassy O'Connor Party Liberal Labor Greens Leader since 20 January 2020 17 March 2017 12 June 2015 Leader's seat Bass Lyons Clark Last election 13 seats; 50.26% 10 seats; 32.63% 2 seats; 10.3% Seats before 12 ...

Genus of flowering plants Borya Borya constricta habit Borya sphaerocephala flower Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Monocots Order: Asparagales Family: Boryaceae Genus: BoryaLabill.[1] Synonyms[1] Baumgartenia Spreng. Daviesia Poir. 1817, illegitimate homonym, not Sm. 1798 Borya is a genus of flowering plants in the family Boryaceae, endemic to Australia.[1] As of July 2013[update], the World Checkli...

Tamari lattice of order 4 In mathematics, a Tamari lattice, introduced by Dov Tamari (1962), is a partially ordered set in which the elements consist of different ways of grouping a sequence of objects into pairs using parentheses; for instance, for a sequence of four objects abcd, the five possible groupings are ((ab)c)d, (ab)(cd), (a(bc))d, a((bc)d), and a(b(cd)). Each grouping describes a different order in which the objects may be combined by a binary operation; in the Tamari lat...

Artikel ini memiliki beberapa masalah. Tolong bantu memperbaikinya atau diskusikan masalah-masalah ini di halaman pembicaraannya. (Pelajari bagaimana dan kapan saat yang tepat untuk menghapus templat pesan ini) Biografi ini memerlukan lebih banyak catatan kaki untuk pemastian. Bantulah untuk menambahkan referensi atau sumber tepercaya. Materi kontroversial atau trivial yang sumbernya tidak memadai atau tidak bisa dipercaya harus segera dihapus, khususnya jika berpotensi memfitnah.Cari sumber:...

English botanist and writer (1688–1732) Richard BradleyBorn1688 (1688)EnglandDied5 November 1732 (aged 43–44)Cambridge, EnglandScientific careerFieldsBotanyInstitutionsUniversity of Cambridge Richard Bradley FRS (1688 – 5 November 1732) was an English naturalist specialising in botany. He published important works on ecology, horticulture, and natural history. Biography The History of succulent plants, 1739 Little is known about Bradley's childhood aside from an early inte...

Real Sporting de GijónCalcio Los Rojiblancos Segni distintiviUniformi di gara Casa Trasferta Terza divisa Colori sociali Rosso, bianco Dati societariCittà Gijón Nazione Spagna ConfederazioneUEFA Federazione FEF CampionatoSegunda División Fondazione1905 Proprietario Grupo Orlegi Presidente Alejandro Irarragorri Allenatore Miguel Ángel Ramírez StadioEl Molinón(29 800 posti) Sito webwww.realsporting.com PalmarèsSi invita a seguire il modello di voce Il Real Sporting de Gijón, ...

Ciliau AeronNoms officiels (en) Ciliau Aeron(cy) Ciliau AeronGéographiePays  Royaume-UniNation constitutive pays de GallesZone principale CeredigionSuperficie 26,6 km2 (2011)Coordonnées 52° 12′ 26″ N, 4° 11′ 47″ ODémographiePopulation 852 hab. (2021)Densité 32 hab./km2 (2021)FonctionnementStatut Village, communautémodifier - modifier le code - modifier Wikidata Ciliau Aeron est un village et une communauté du Ceredigion,...

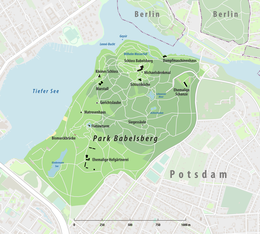
UNESCO World Heritage Site in Brandenburg, Germany Babelsberg ParkUNESCO World Heritage SiteBabelsberg ParkLocationPotsdam, Brandenburg, GermanyPart ofPalaces and Parks of Potsdam and BerlinCriteriaCultural: (i), (ii), (iv)Reference532terInscription1990 (14th Session)Extensions1992, 1999Coordinates52°24′19″N 13°05′34″E / 52.405386°N 13.092721°E / 52.405386; 13.092721Location of Babelsberg Park in BrandenburgShow map of BrandenburgBabelsberg Park (Germa...

Russian noble Grand Duke Michael NikolaevichMichael Nikolaevich, c. 1880–90Born(1832-10-25)25 October 1832Peterhof Palace, Saint Petersburg, RussiaDied18 December 1909(1909-12-18) (aged 77)Cannes, Alpes-Maritimes, FranceSpouse Princess Cecilie of Baden ​ ​(m. 1857; died 1891)​Issue Grand Duke Nicholas Mikhailovich Anastasia Mikhailovna, Grand Duchess of Mecklenburg-Schwerin Grand Duke Michael Mikhailovich Grand Duke George Mikhailov...