Metro Montreal

Montreal Metro
Dari kiri atas, searah jarum jam: Pintu masuk di Square-Victoria-OACI, Bagian dalam kereta Azur yang tiba tahun 2014, Kereta MR-73 di Stasiun Montmorency, Mural keramik di Stasiun Crémazie, Dua kereta MR-73 di Stasiun Plamondon
Info
WilayahMontreal, Quebec, Kanada
JenisAngkutan cepat
Jumlah jalur4
Jumlah stasiun68
Penumpang harian1.245.700 (rata-rata harian,
Q1 2014)[1]
Penumpang tahunan356.096.000 (2013)[2]
Operasi
Dimulai14 Oktober 1966
OperatorSociété de transport de Montréal
Jumlah gerbong759
Teknis
Panjang sistem692 km (430 mi)[3][4]
Lebar sepur1.435 mm (4 ft 8+1⁄2 in) sepur standar
with running pads for the rubber
tired wheels outside of the steel rails
Listrik"Third rail", 750 V DC on the guide bars at either side of the track
Kecepatan rata-rata40 km/h (25 mph)
Kecepatan tertinggi72 km/h (45 mph)

Montreal Metro (bahasa Prancis: Métro de Montréal) adalah sistem angkutan cepat di kota Montreal, Quebec, Kanada.

Metro ini dioperasikan oleh Société de transport de Montréal (STM), diresmikan tanggal 14 Oktober 1966. Awalnya terdiri dari 26 stasiun, saat ini sudah berkembang menjadi 68 stasiun dengan panjang total 692 kilometer (430 mi),[3][4] melayani kawasan utara, timur, dan pusat Pulau Montreal dengan koneksi ke Longueuil via Jalur Kuning, dan Laval via Jalur Jingga.

Montreal Metro adalah angkutan cepat tersibuk di Kanada, dan ketiga tersibuk di Amerika Utara dari jumlah penumpang setelah New York City dan Mexico City. Jumlah penumpang harian sekitar 1.245.700,[1] sedangkan total penumpang tahunan adalah 356.1 juta (2013).[2]

Referensi

Catatan

  1. ^ a b "Transit Ridership Report, First Quarter, 2014" (PDF). American Public Transportation Association. May 21, 2014. hlm. 32. Diakses tanggal 2014-07-24. 
  2. ^ a b "Transit Ridership Report, Fourth Quarter, 2013" (PDF). American Public Transportation Association. February 14, 2014. hlm. 31. Diakses tanggal 2014-07-24. 
  3. ^ a b Montreal Metro at urbanrail.net
  4. ^ a b Montreal Metro at metrobits.org

Pranala luar

Wikimedia Commons memiliki media mengenai Montreal metro.

Read other articles:

Complesso di Edipo

Il complesso di Edipo è un concetto originariamente sviluppato nell'ambito della teoria psicoanalitica da Sigmund Freud, che ispirò anche Carl Gustav Jung (fu lui a descrivere il concetto e a coniare il termine complesso), per spiegare la maturazione del bambino attraverso l'identificazione col genitore del proprio sesso e il desiderio nei confronti del genitore del sesso opposto. Si basa sul mito greco di Edipo, che, a sua insaputa, uccise suo padre Laio e, altrettanto inconsapevolmente, s...

 

Danau Kaindy

Danau KaindyҚайыңды көліDanau KaindyLokasi di KazakhstanKoordinat42°59′15″N 78°27′50″E / 42.98750001°N 78.4638888989°E / 42.98750001; 78.4638888989Koordinat: 42°59′15″N 78°27′50″E / 42.98750001°N 78.4638888989°E / 42.98750001; 78.4638888989Terletak di negaraKazakhstanPanjang maksimal400 mKedalaman maksimal30 mKetinggian permukaan2.000 m Danau Kaindy (Қайыңды көлі, Qayıñdı köli) adalah sebuah dana...

 

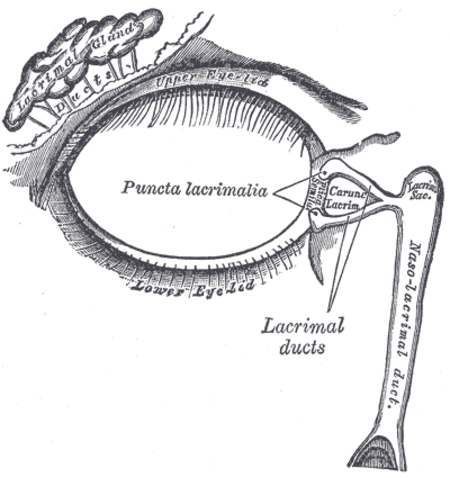
Kelenjar air mata

Aparatus lakrimal dari mata kanan Kelenjar air mata atau kelenjar lakrimalis adalah kelenjar di mata yang mengeluarkan air mata.[1] Kelenjar lakrimalis terletak pada bagian lateral atas mata yang disebut dengan fossa lakrimalis.[2] Bagian utama kelenjar ini bentuk dan ukuranya mirip dengan biji almond, yang terhubung dengan suatu penonjolan kecil yang meluas hingga ke bagian posterior dari palpebra superior.[2] Dari kelenjar ini, air mata diproduksi dan kemudian dialir...

Ayya Vaikundar

Indian avatar This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (March 2021) (Learn how and when to remove this template message) The neutrality of this article is disputed. Relevant discussion may be found on ...

 

Синелобый амазон

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

 

Кубок

У этого термина существуют и другие значения, см. Кубок (значения). Кубок Ку́бок[1] (др.-греч. κύβος) — сосуд для питья вина, пива, мёда или медовухи. Чаще всего металлический, но нередко делался из кости или стекла, украшался орнаментом и драгоценными камнями. В средневек...

Battaglia di Hampton Roads

Battaglia di Hampton Roadsparte della campagna Peninsulare della guerra di secessione americanaFotografia dello scontro tra la CSS Virginia e la USS Monitor, primo giorno di battagliaData8-9 marzo 1862 LuogoHampton Roads, Virginia, Stati Uniti orientali EsitoNon decisiva Schieramenti Stati Uniti d'America Stati Confederati d'America Comandanti Louis M. Goldsborough John Marston Franklin Buchanan Catesby ap Roger Jones Effettivi Union Navy:1 nave corazzata5 fregate Confederate States Navy:1 na...

 

Counts and Dukes of Angoulême

Angoulême (L'Angoumois) in western France was part of the Carolingian Empire as the kingdom of Aquitaine. Under Charlemagne's successors, the local Count of Angoulême was independent and was not united with the French crown until 1308. By the terms of the Treaty of Brétigny (1360) the Angoumois, then ruled by the Counts of Angoulême, was ceded as English territory to Edward III. In 1371 it became a fief of the Duke of Berry, before passing to Louis I, Duke of Orleans, both of whom were ca...

 

Podstrana

Cet article est une ébauche concernant une localité croate. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Podstrana Héraldique Podstrana – Vue Administration Pays Croatie Comitat Split-Dalmatie Maire Mandat Mario Tomasović 2005-2009 Code postal 21312 Indicatif téléphonique international +(385) Indicatif téléphonique local 021 Démographie Population 10 403 hab. (2021) Densité 889 hab....

BASIC Stamp

Microcontrollers Diagram of a BASIC Stamp 2 The BASIC Stamp is a microcontroller with a small, specialized BASIC interpreter (PBASIC) built into ROM. It is made by Parallax, Inc. and has been popular with electronics hobbyists since the early 1990s. Technical specifications Although the BASIC Stamp 2 has the form of a 24 pin DIP chip, it is in fact a small printed circuit board (PCB) that contains the essential elements of a microprocessor system:[1] A Microcontroller containing the C...

 

2020年夏季奥林匹克运动会马来西亚代表团

2020年夏季奥林匹克运动会马来西亚代表團马来西亚国旗IOC編碼MASNOC马来西亚奥林匹克理事会網站olympic.org.my（英文）2020年夏季奥林匹克运动会（東京）2021年7月23日至8月8日（受2019冠状病毒病疫情影响推迟，但仍保留原定名称）運動員30參賽項目10个大项旗手开幕式：李梓嘉和吳柳螢（羽毛球）[1][2]閉幕式：潘德莉拉（跳水）[3]獎牌榜排名第74 金牌 銀牌 銅�...

 

哈萨克斯坦总统

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言，清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日（哈薩克蘇維埃社會主義共和國總統） 哈萨克斯坦 哈萨克斯坦政府...

哈萨克斯坦总统

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言，清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日（哈薩克蘇維埃社會主義共和國總統） 哈萨克斯坦 哈萨克斯坦政府...

 

Timi

Thyme Broad leaved Thyme Thymus pulegioides Klasifikasi ilmiah Kerajaan: Plantae (tanpa takson): Tracheophyta (tanpa takson): Angiospermae (tanpa takson): Eudikotil (tanpa takson): Asterid Ordo: Lamiales Famili: Lamiaceae Genus: ThymusL. Spesies Terdiri 350 spesies, termasuk: Thymus adamovicii Thymus altaicus Thymus amurensis Thymus bracteosus Thymus broussonetii Thymus caespititius Thymus camphoratus Thymus capitatus Thymus capitellatus Thymus camphoratus Thymus carnosus Thymus cephalotus T...

 

Landkreis Oppeln

Der Landkreis Oppeln auf einer Karte von 1905 Lage des Landkreises in der Provinz Oberschlesien Der Landkreis Oppeln war ein preußischer Landkreis in Schlesien, der in den Jahren 1743 bis 1945 bestand. Seine Kreisstadt war die Stadt Oppeln, die seit 1899 einen eigenen Stadtkreis bildete. Das ehemalige Kreisgebiet liegt heute in der polnischen Woiwodschaft Oppeln. Inhaltsverzeichnis 1 Verwaltungsgeschichte 2 Einwohnerentwicklung 3 Landräte 4 Kommunalverfassung 5 Gemeinden 6 Ortsnamen 7 Liter...

Newark Bay

Estuary in northeastern New Jersey, US For the bay on the island of South Georgia, see Newark Bay (South Georgia). Newark BayPort Newark is seen in the foreground looking northeast across the bay to Jersey City and the Manhattan borough of New York City.Newark BayShow map of Hudson County, New JerseyNewark BayShow map of New JerseyNewark BayShow map of the United StatesLocationNew JerseyCoordinates40°40′47″N 74°07′53″W / 40.679597°N 74.131451°W / 40.679597;...

 

Arthur Herbert, 1st Earl of Torrington

17th and 18th-century Royal Navy admiral For other people with the same name, see Arthur Herbert (disambiguation). The Right HonourableThe Earl of TorringtonArthur Herbert, 1st Earl of Torrington, portrait by John ClostermanBornc.1648Died13 April 1716 (aged 67–68)[1]BuriedWestminster AbbeyAllegiance Kingdom of EnglandService/branch Royal NavyYears of service1663–1690RankAdmiralCommands heldHMS PembrokeHMS Constant WarwickHMS DragonHMS DreadnoughtHMS Cambrid...

 

What It Is (Mark Knopfler song)

2000 single by Mark KnopflerWhat It IsSingle by Mark Knopflerfrom the album Sailing to Philadelphia Released4 September 2000 (2000-09-04)GenreRoots rockLength4:57 (Album version) 3:33 (Radio edit) 5:36 (Mexican version)Songwriter(s)Mark KnopflerProducer(s)Mark KnopflerMark Knopfler singles chronology Rüdiger (1996) What It Is (2000) Sailing To Philadelphia (2000) What It Is is a song written and recorded by the British rock musician Mark Knopfler. It was released on 4 Septemb...

Kyōsuke Kindaichi

Kyōsuke Kindaichi Kyōsuke Kindaichi (金田一 京助code: ja is deprecated , Kindaichi Kyōsuke, 5 Mei 1882 – 14 November 1971) adalah seorang ahli bahasa dari Morioka, Prefektur Iwate, Jepang. Dia dikenal karena diktat-nya tentang yukar, atau saga dari bangsa Ainu. Ahli bahasa Haruhiko Kindaichi adalah anaknya. Kindaichi juga aktif sebagai penulis puisi dan memiliki hubungan yang baik dengan Ishikawa Takuboku. Dia juga merupakan penulis dari kamus Meikai Kokugo Jiten. Penghargaan Order ...

 

Mathematical induction

Form of mathematical proof Not to be confused with inductive reasoning. Mathematical induction can be informally illustrated by reference to the sequential effect of falling dominoes.[1][2] Mathematical induction is a method for proving that a statement P ( n ) {\displaystyle P(n)} is true for every natural number n {\displaystyle n} , that is, that the infinitely many cases P ( 0 ) , P ( 1 ) , P ( 2 ) , P ( 3 ) , … {\displaystyle P(0),P(1),P(2),P(3),\dots }   all...