Matriks Hesse
|
Read other articles:

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Belanja tidak terduga adalah pengeluaran anggaran untuk kegiatan yang sifatnya tidak biasa dan tidak diharapkan berulang seperti penanggulangan bencana alam, bencana sosial, dan pengeluaran tidak terduga lainnya yang sangat diperlukan dalam rangka pen...

Bagian dari seriPendidikan di Indonesia Kementerian Pendidikan, Kebudayaan, Riset, dan Teknologi Republik Indonesia Pendidikan anak usia dini TK RA KB Pendidikan dasar (kelas 1–6) SD MI Paket A Pendidikan dasar (kelas 7–9) SMP MTs Paket B Pendidikan menengah (kelas 10–12) SMA MA SMK MAK SMA SMTK SMAK Utama Widya Pasraman Paket C Pendidikan tinggi Perguruan tinggi Akademi Akademi komunitas Institut Politeknik Sekolah tinggi Universitas Lain-lain Madrasah Pesantren Sekolah alam Sekolah ru...

Mosaik Romawi yang menggambarkan Orfeus di vila dari masa Kekaisaran Romawi akhir. Orfisme (disebut juga Orfikisme) (Greek: Ὀρφικάcode: el is deprecated ) adalah nama yang diberikan pada seperangkat kepercayaan dan praktik keagamaan[1] di dunia Yunani kuno dan Helenistik,[2][3][4][5] selain juga oleh orangorang Thrakia,[6] dihubungkan dengan penyair mitis Orfeus, yang turun ke dunia bawah dan kembali. Orang-orang Orfik juga memuja Persefo...

جوستافو نوبوا (بالإسبانية: Gustavo José Noboa Bejarano) مناصب حاكم غاياس في المنصبمارس 1983 – 10 أغسطس 1984 خوان بابلو مونكاغاتا [لغات أخرى] خايمي نيبوت [لغات أخرى] عميد في المنصب1986 – 1996 في جامعة سانتياغو دي غواياكيل الكاثوليكية ...

Village in Estonia For the concept in Mandaeism, see Laufa. Village in Järva County, EstoniaLaupaVillageLaupa ManorLaupaCoordinates: 58°45′30″N 25°22′10″E / 58.75833°N 25.36944°E / 58.75833; 25.36944Country EstoniaCountyJärva CountyParishTüri ParishTime zoneUTC+2 (EET) • Summer (DST)UTC+3 (EEST) Laupa is a village in Türi Parish, Järva County in central Estonia.[1] Laupa manor Laupa estate was established at the beginning of th...

For the museum in Algeria, see Bardo National Museum (Algiers). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Bardo National Museum Tunis – news · newspapers · books · scholar · JSTOR (June 2019) (Learn how and when to remove this message) National museum in Tunis, TunisiaBardo National MuseumArabic: ...
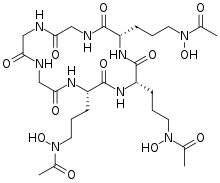
Structure of the siderophore triacetylfusarinine encapsulating iron(III) within a tris(hydroxamate) coordination sphere (color code: red = oxygen, gray = carbon, blue = nitrogen, dark blue = iron).[1] Iron compounds secreted by microorganisms Siderophores (Greek: iron carrier) are small, high-affinity iron-chelating compounds that are secreted by microorganisms such as bacteria and fungi. They help the organism accumulate iron.[2][3][4][5] Although a wi...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目可能包含原创研究。 (2018年3月29日)请协助補充参考资料、添加相关内联标签和删除原创研究内容以改善这篇条目。详细情况请参见讨论页。 此條目需要补充更多来源。 (2010年2月4日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一�...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府(Oguzkhan Presidential Palace)機關所在地阿什哈巴德任命者直接选举任期7年,可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關(英语:National Council of Turkmenistan) ...

مريم فخر الدين (بالعربية: مريم فخر الدين) معلومات شخصية اسم الولادة (بالعربية: مريم محمد فخر الدين) الميلاد 8 سبتمبر 1933 الفيوم الوفاة 3 نوفمبر 2014 (81 سنة) القاهرة سبب الوفاة سكتة دماغية مواطنة مصر الزوج فهد بلانمحمود ذو الفقار الأولاد إيمان ذو ...

Stasiun Aioiyama相生山駅Lokasi61, Aikawa 3-chōme, Midori, Nagoya, Aichi(名古屋市緑区相川3丁目61)JepangKoordinat35°06′09″N 136°58′34″E / 35.102545°N 136.976208°E / 35.102545; 136.976208Koordinat: 35°06′09″N 136°58′34″E / 35.102545°N 136.976208°E / 35.102545; 136.976208OperatorBiro Transportasi Kota NagoyaJalurJalur SakuradōriLayanan Pemberhentian bus Informasi lainKode stasiunS19SejarahDibuka2011Sunting...

British television series For other books, series and films in the Tracy Beaker franchise, see The Story of Tracy Beaker (franchise). The Story of Tracy BeakerThe Story of Tracy Beaker title cardCreated byJacqueline Wilson (Books)Based onThe Story of Tracy BeakerStarringList of Tracy Beaker series charactersOpening themeSomeday sung by Keisha WhiteCountry of originUnited KingdomOriginal languageEnglishNo. of series5No. of episodes120 + 5 specials (list of episodes)ProductionExecutive producer...

Ongoing COVID-19 pandemic in North Korea This article needs to be updated. Please help update this article to reflect recent events or newly available information. (December 2022) COVID-19 pandemic in North KoreaDiseaseCOVID-19Virus strainSARS-CoV-2LocationNorth KoreaFirst outbreakWuhan, Hubei, ChinaIndex casePyongyangArrival date8 May 2022 (2022-05-08) (2 years, 1 month and 6 days ago)[1]Confirmed cases168[2]Deaths74[a][3][4&#...

American basketball coach and sportscaster (born 1933) Hubie BrownBrown in 1981Personal informationBorn (1933-09-25) September 25, 1933 (age 90)Hazleton, Pennsylvania, U.S.Listed height6 ft 0 in (1.83 m)Listed weight160 lb (73 kg)Career informationHigh schoolSt. Mary (Elizabeth, New Jersey)CollegeNiagara (1951–1955)NBA draft1955: undraftedPlaying career1958–1959Coaching career1955–1987, 2002–2004Career historyAs player:1958–1959Rochester ColonelsAs coac...

В Википедии есть статьи о других людях с такой фамилией, см. Евланов. Владимир Лазаревич Евланов Глава города Краснодара 22 сентября 2005 — 8 декабря 2016 Президент Владимир ПутинДмитрий Медведев Губернатор Александр ТкачёвВениамин Кондратьев Предшественник Николай Приз...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (فبراير 2016) هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحس...

Primera División Uruguaya 1976 Competizione Primera División Uruguaya Sport Calcio Edizione 73ª Organizzatore AUF Luogo Uruguay Partecipanti 12 Formula 1 girone all'italiana Risultati Vincitore Defensor(1º titolo) Statistiche Miglior marcatore Fernando Morena (18) Incontri disputati 132 Gol segnati 360 (2,73 per incontro) Cronologia della competizione 1975 1977 Manuale Il campionato era formato da dodici squadre e il Defensor vinse il titolo. Classifica finale Pos. ...

Polish football club Football clubRuch RadzionkówFull nameKlub SportowyRuch RadzionkówNickname(s)CidryFounded14 August 1919; 104 years ago (1919-08-14) (as Towarzystwo Gier i Zabaw Radzionków)[1]2012; 12 years ago (2012) (refounded)GroundSMS RadzionkówCapacity532ChairmanWitold WieczorekManagerMarcin TrzcionkaLeagueIV liga Silesia2023–24IV liga Silesia I, 4th of 16WebsiteClub website Home colours Away colours Ruch Radzionków is a Polish associ...

Un gruppo di AD di Fortune 500 nel 2015. L'amministratore delegato (AD), anche consigliere delegato (CD), è un componente del consiglio di amministrazione di una società per azioni, società di persone o altra azienda organizzata in modo analogo, a cui sono stati conferiti dal consiglio stesso ampi poteri decisionali sulle azioni e sulla struttura dell'attività aziendale, e che svolge un ruolo di preminenza al suo interno. Indice 1 Caratteristiche generali 2 Nel mondo 2.1 Giappone 2.2 Ital...
![{\displaystyle \mathbf {H} f={\begin{bmatrix}{\dfrac {\partial ^{2}f}{\partial x_{1}^{2}}}&{\dfrac {\partial ^{2}f}{\partial x_{1}\,\partial x_{2}}}&\cdots &{\dfrac {\partial ^{2}f}{\partial x_{1}\,\partial x_{n}}}\\[2.2ex]{\dfrac {\partial ^{2}f}{\partial x_{2}\,\partial x_{1}}}&{\dfrac {\partial ^{2}f}{\partial x_{2}^{2}}}&\cdots &{\dfrac {\partial ^{2}f}{\partial x_{2}\,\partial x_{n}}}\\[2.2ex]\vdots &\vdots &\ddots &\vdots \\[2.2ex]{\dfrac {\partial ^{2}f}{\partial x_{n}\,\partial x_{1}}}&{\dfrac {\partial ^{2}f}{\partial x_{n}\,\partial x_{2}}}&\cdots &{\dfrac {\partial ^{2}f}{\partial x_{n}^{2}}}\end{bmatrix}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/053f4c9c57f34ff20e3cb5d45204965061ca39b8)

