Kekekalan energi
|
Read other articles:

Gregorius Palamas Gregorius Palamas dikenal sebagai seorang tokoh pengusung Teologi Hesikhasme.[1] Hesikhasme berasal dari kata bahasa Yunani hesykia yang berarti keheningan, kesepian, istirahat.[1] Ini adalah sebuah tradisi spiritual yang sudah ada sejak zaman gereja purba.[1] Tujuannya adalah untuk mencapai keheningan batin sehingga dapat tiba para perenungan akan Allah.[1] Gregorius Palamas lahir pada akhir abad ke-13.[1] Ia belajar untuk menjadi seo...

Halaman ini berisi artikel tentang parpol Eropa yang didirikan tahun 1992. Untuk Kelompok Sosialis & Demokrat di Parlemen Eropa, lihat Aliansi Progresif dari Sosialis dan Demokrat. Partai Sosialis Eropa Presiden Stefan LöfvenSekretaris Jenderal Achim PostDibentuk1973 (Konfederasi)9–10 November 1992 (Partai)Kantor pusatRue du Trône/Troonlaan 98, 1050 Brussel, BelgiaWadah pemikirFoundation for European Progressive StudiesSayap pemudaSosialis Eropa MudaSayap wanitaPES WomenIdeologiDemokr...
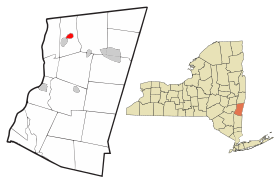
فالاتي الإحداثيات 42°24′50″N 73°40′39″W / 42.4139°N 73.6775°W / 42.4139; -73.6775 [1] تاريخ التأسيس 1665 تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة كولومبيا خصائص جغرافية المساحة 3.279609 كيلومتر مربع3.279608 كيلومتر مربع (1 أبريل 2010) ا...

Government tourism promotion agencySingapore Tourism BoardAgency overviewFormed1 January 1964; 60 years ago (1964-01-01) (as Singapore Tourist Promotion Board)19 November 1997; 26 years ago (1997-11-19) (as Singapore Tourism Board)JurisdictionGovernment of SingaporeHeadquartersTourism Court, 1 Orchard Spring Lane, Singapore 247729Agency executivesOlivier Lim, Chairman[1]Melissa Ow, CEO[2]Parent agencyMinistry of Trade and IndustryWebsitewww...

متنزه يلوستون الوطني IUCN التصنيف II (حديقة وطنية) البلد الولايات المتحدة سميت باسم نهر يلوستون الموقع وايومنغ، وأيداهو، ومونتانا الجهة ولايات أيداهو ومونتانا ووايومنغ إحداثيات 44°36′53″N 110°30′03″W / 44.614722°N 110.500833°W / 44.614722; -110.500833 المساحة 8983 كم2 ...

Frequency that a song is broadcast on radio stations This article is about the radio term. For the Apple software, see AirPlay. For other uses, see Airplay (disambiguation). The examples and perspective in this article may not represent a worldwide view of the subject. You may improve this article, discuss the issue on the talk page, or create a new article, as appropriate. (January 2020) (Learn how and when to remove this template message) A radio DJ playing music Airplay is how frequently a...

Classe Flyvefisken[1] Le P555 Støren configuré en patrouilleur. Standard Flex 300 ou StanFlex 300Classe Tejo Caractéristiques techniques Type Navire militaire polyvalent Longueur 54 m Maître-bau 9 m Tirant d'eau 2.60 m Déplacement 320 t À pleine charge ~ 450 t Propulsion 2 diesels MTU 16V 396TB94 1 turbine à gaz General Electric LM500 Vitesse 30 nœuds (55 km/h) Caractéristiques militaires Armement 4 emplacements pour module StanFlex 2 mitrailleuses 12,7 mm Rayon d’action 2400 naut...

Questa voce sull'argomento stagioni delle società calcistiche italiane è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Voce principale: Società Sportiva Monopoli 1966. Associazione Calcio MonopoliStagione 2007-2008Sport calcio Squadra Monopoli Allenatore Sauro Trillini poi Arcangelo Sciannimanico poi Sauro Trillini poi Giovanni Sasanelli Presidente Domenico Ladisa Serie C26º posto nel girone C....

Artikel biografi ini ditulis menyerupai resume atau daftar riwayat hidup (Curriculum Vitae). Tolong bantu perbaiki agar netral dan ensiklopedis.Benny Dwifa Yuswir Bupati Sijunjung ke-19PetahanaMulai menjabat 26 Februari 2021PresidenJoko WidodoGubernurMahyeldiWakilIraddatillahPendahuluYuswir ArifinZefnihan (Plh.)PenggantiPetahana Informasi pribadiLahir13 Januari 1986 (umur 38)Muaro, Sumatera BaratPartai politikGolkarSuami/istriNedia Fitri GuspardiAnak3Orang tuaYuswir Arifin (ayah)...

В этом китайском имени фамилия (Гуань) стоит перед личным именем. Гуань Юй Дата рождения 160 Место рождения Яньху, округ Хэдун[d], Империя Хань Дата смерти январь 220 Место смерти Линьцзюй, провинция Цзинчжоу Страна Восточная Хань[d] Род деятельности офицер, армей�...

Marienetta JirkowskyMarienetta Jirkowsky, di Jendela Kenangan, Monumen Tembok Berlin, Bernauer Straße.Lahir(1962-08-25)25 Agustus 1962Bad Saarow, Jerman TimurMeninggal22 November 1980(1980-11-22) (umur 18)Hennigsdorf, Jerman TimurSebab meninggalDitembak oleh seorang garda saat berniat untuk masuk Berlin Barat dari Hohen Neuendorf, yang berada di bekas RDJPenemuan jasadProperti lowong di Florastrasse52°39′38″N 13°17′05″E / 52.6605°N 13.2846°E / 5...

American screenwriter and producer Dan FogelmanFogelman at the premiere of Life Itself, 2018 Toronto International Film FestivalBorn (1976-02-19) February 19, 1976 (age 48)River Vale, New Jersey, U.S.Alma materUniversity of PennsylvaniaOccupation(s)screenwriter, producerKnown for Cars Bolt Tangled Crazy, Stupid, Love This Is Us Spouse Caitlin Thompson (m. 2015)Children1[1] Dan Fogelman (born February 19, 1976) is an American screenwriter a...

Struktur Hell in a Cell pada acara Hell in a Cell bulan Oktober 2017 Hell in a Cell adalah pertandingan berbasis kerangkeng baja gulat profesional yang berasal dari tahun 1997 di World Wrestling Federation (WWF, sekarang WWE). Pertandingan ini menampilkan struktur sel besar berbentuk kubus lima sisi yang terbuat dari pagar rantai-link baja terbuka yang membungkus area ring dan sisi ring. Berbeda dengan pertandingan steel cage, satu-satunya cara untuk keluar dari Hell in a Cell tanpa merusak s...

Jalan Petaling. Jalan Petaling (Tamilபெட்டாலிங் தெரு , Peṭṭāliṅ teru) , atau lebih dikenal dengan panggilan Petaling Street, merupakan kawasan pecinan di Kuala Lumpur, Malaysia. Selama bertahun-tahun lamanya, Jalan Petaling telah menjadi tempat bisnis dan pelestarian budaya dan tradisi masyarakat Cina di Malaysia, dengan kuil Buddha dan toko yang menjual colok, obat tradisional, dan makanan Tionghoa. Pada awal petang hingga lewat malam, penjaja akan menjual ...

The Paget Gorman Sign System, also known as Paget Gorman Signed Speech (PGSS) or Paget Gorman Systematic Sign Language is a manually coded form of the English language, designed to be used with children with speech or communication difficulties. Development PGSS was originally developed in Britain by anthropologist Sir Richard Paget in the 1930s, [1] and later by his wife Lady Grace Paget and Dr Pierre Gorman.[2] The system is founded on the notion that the original form of al...

Airport in Highland County, Florida Avon Park Executive Airport2006 USGS airphotoIATA: AVOICAO: KAVOFAA LID: AVOSummaryAirport typePublicOwnerCity of Avon ParkServesAvon Park, FloridaElevation AMSL160 ft / 49 mCoordinates27°35′29″N 81°31′44″W / 27.59139°N 81.52889°W / 27.59139; -81.52889Websitewww.avonpark.city/..MapAVOLocation of airport in FloridaShow map of FloridaAVOAVO (the United States)Show map of the United StatesRunways Direction Len...

City in Derbyshire, England This article is about the city in England. For other uses, see Derby (disambiguation). City and unitary authority in EnglandDerbyCity and unitary authorityFrom left to right:Top: Victoria StreetMiddle: Sadler Gate and the Market HallBottom: Council House and All Saints' Cathedral Coat of armsMotto(s): Latin: Industria, Virtus et Fortitudo, lit. 'Energy, Power and Strength'Shown within DerbyshireCoordinates: 52°55′29″N 1°28′41″W ...

Untuk kegunaan lain, lihat Interpol (disambiguasi). Organisasi Polisi Kriminalitas InternasionalInternational Criminal Police OrganizationOrganisation internationale de police criminelleNamaInterpolSingkatanICPO-INTERPOLMottoConnecting police for a safer world(Menghubungkan polisi untuk dunia yang lebih aman)IkhtisarDibentuk1923; 101 tahun lalu (1923)PendahuluKongres Polisi Kriminalitas Internasional Pertama (1914)Konferensi Polisi Internasional (1922)Komisi Polisi Kriminalitas Internasi...

National anthem of Abkhazia AiaairaEnglish: VictoryАиааираSheet musicNational anthem of AbkhaziaLyricsGennady AlamiaMusicValery ChkaduaAdopted24 October 2007Audio sampleOfficial orchestral and choral vocal recordingfilehelp Other official recordings Orchestral and choral vocal recording (short version) Orchestral instrumental recording Orchestral instrumental recording (short version) Orchestral instrumental recording (short version) (version 2) Piano and choral vocal recording Pr...

Luv Ki Arrange MarriagePoster rilis resmiSutradaraIshrat R. KhanProduserVinod BhanushaliKamlesh Bhanushali Raaj ShaandilyaaVimal LahotiDitulis olehRaaj ShaandilyaaPemeranSunny SinghAvneet KaurAnnu KapoorSupriya PathakPenata musikPrini Siddhant MadhavAmol-AbhishekJaidev KumarSadhu S. TiwariMeet BrosSandesh ShandilyaSinematograferArun PrasadPerusahaanproduksiBhanushali StudiosThinkink PicturezDistributorZEE5Tanggal rilis 14 Juni 2024 (2024-06-14) Durasi120 menitNegaraIndiaBahasaHindi...
















