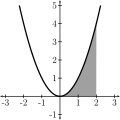
Jumlah Riemann
|
Read other articles:

Västra Götaland Västra Götalands länDaerah di Swedia Lambang kebesaran CountrySwediaIbu kotaGothenburgPemerintahan • GubernurLars Bäckström • DewanVästra Götaland Regional DewanLuas • Total23.945 km2 (9,245 sq mi)Populasi (March 31 2011)[1] • Total1.589.016 • Kepadatan66/km2 (170/sq mi)Zona waktuUTC+1 (CET) • Musim panas (DST)UTC+2 (CEST)GDP/ NominalSEK 386,538 million (2004)...

Johannes Wurtz Wurtz bermain untuk 1. FC SaarbrückenInformasi pribadiTanggal lahir 19 Juni 1992 (umur 31)Tempat lahir Saarbrücken, JermanTinggi 1,83 m (6 ft 0 in)Posisi bermain PenyerangInformasi klubKlub saat ini Werder BremenNomor 27Karier junior0000–2005 DJK Bexbach2005–2010 1. FC SaarbrückenKarier senior*Tahun Tim Tampil (Gol)2010–2011 1. FC Saarbrücken II 3 (1)2011–2012 1. FC Saarbrücken 36 (9)2012– Werder Bremen II 15 (9)2012– Werder Bremen 0 (0)Tim...

Amerika Serikat padaOlimpiadeBendera Amerika SerikatKode IOCUSAKONKomite Olimpiade & Paralimpiade Amerika SerikatMedali 1.127 907 793 Total 2,827 Penampilan Musim Panas18961900190419081912192019241928193219361948195219561960196419681972197619801984198819921996200020042008201220162020Penampilan Musim Dingin192419281932193619481952195619601964196819721976198019841988199219941998200220062010201420182022Penampilan terkait lainnyaOlimpiade Interkala 1906 Berikut ini adalah daftar pembawa bende...

Pour les articles homonymes, voir Barthélemy. Joseph BarthélemyJoseph Barthélemy en 1942.FonctionsGarde des Sceaux, ministre de la Justice27 janvier 1941 - 26 mars 1943Conseiller général du Gers1922-1945Député du Gers16 novembre 1919 - 31 mai 1928Maire de L'Isle-JourdainBiographieNaissance 9 juillet 1874ToulouseDécès 14 mai 1945 (à 70 ans)AuchSépulture CassemartinNationalité françaiseActivités Homme politique, juriste, politologuePère Aimé BarthélemyAutres informationsA...

سمير الملا معلومات شخصية الميلاد يناير 1940 القاهرة تاريخ الوفاة 6 سبتمبر 2021 (80–81 سنة)[1] مواطنة المملكة المصرية (1940–1953) جمهورية مصر (1953–1958) الجمهورية العربية المتحدة (1958–1971) مصر (1971–2021) الحياة العملية المدرسة الأم جامعة عين شمس (الشهادة:بكالوريوس الطب وا�...

For other uses, see North Coast. Region in New South Wales, AustraliaMid North CoastNew South WalesMcBrides Beach, Forster, New South WalesMid North CoastCoordinates31°16′S 152°54′E / 31.267°S 152.900°E / -31.267; 152.900Population308,372 (30 June 2016)[1] • Density14.4187/km2 (37.3442/sq mi)Area21,387 km2 (8,257.6 sq mi)Time zoneAEST (UTC+10) • Summer (DST)AEDT (UTC+11)LGA(s) Bellingen Shire City of Coffs Harbour ...

1991 bombing of a civilian shelter in Baghdad, Iraq by the US during the Gulf War Amiriyah shelter bombingPart of the Gulf WarInterior of the shelter, currently maintained as a memorial to the bombingTypeAirstrikeLocationAl-A'amiriya, Baghdad, Iraq33°17′50″N 44°16′50″E / 33.29722°N 44.28056°E / 33.29722; 44.28056DateFebruary 13, 1991 (1991-02-13)Executed by United States Air ForceCasualties408+ killedUnknown injuredAl-A'amiriyaLocation o...

Keakuratan artikel ini diragukan dan artikel ini perlu diperiksa ulang dengan mencantumkan referensi yang dapat dipertanggungjawabkan. Diskusi terkait dapat dibaca pada the halaman pembicaraan. Harap pastikan akurasi artikel ini dengan sumber tepercaya. Lihat diskusi mengenai artikel ini di halaman diskusinya. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Fondue keju dari Swiss. Fondue adalah suatu hidangan yang dinikmati dengan cara mencelupkan potongan makanan ke dalam...

For the mutiny, see Yên Bái mutiny. The failure of the Yên Bái mutiny by Vietnamese soldiers in the French colonial army on February 10, 1930, caused the French authorities to engage in a reform of military policies which were aimed at preventing future uprisings. French trust in the Vietnamese soldiers' loyalty as colonised subjects who were simultaneously enforcers of colonial order had never been high, and the mutiny resulted in increased safeguards against Vietnamese soldiers in an at...

Questa voce sugli argomenti arene di pallacanestro degli Stati Uniti d'America e stadi del ghiaccio è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Questa voce sull'argomento architetture di Boston è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. TD GardenThe Garden, The Vault Informazioni generaliStato Stati Uniti Ubicazione100 Legends WayBoston, Massachusetts 02114 Inizio lavorimaggio 1993 Inaugurazione30...

PracuúbaMunisipalitasNegara BrasilNegara bagianAmapáLuas • Total4.956,477 km2 (1,913,706 sq mi)Populasi (2010) • Total3.793 • Kepadatan0,00.077/km2 (0,0.020/sq mi) Pracuúba merupakan sebuah munisipalitas yang terletak di negara bagian Brasil di Amapá. lbs Munisipalitas di AmapáIbu kota: MacapáAmapá Amapá Pracuúba Tartarugalzinho Macapá Cutias Ferreira Gomes Itaubal Macapá Pedra Branca do Amapari Porto Grande Santana Serra...

Former Prime Minister of Belgium and President of the European Council Van Rompuy redirects here. For other uses, see Van Rompuy (disambiguation). In this Dutch name, the surname is Van Rompuy, not Rompuy. The Count Van RompuyOfficial portrait, 2012President of the European CouncilIn office1 December 2009 – 30 November 2014Preceded byFredrik Reinfeldt (non-permanent)Succeeded byDonald TuskPrime Minister of BelgiumIn office30 December 2008 – 25 November 2009MonarchAlbert ...

Number that is not a ratio of integers The number √2 is irrational. In mathematics, the irrational numbers (in- + rational) are all the real numbers that are not rational numbers. That is, irrational numbers cannot be expressed as the ratio of two integers. When the ratio of lengths of two line segments is an irrational number, the line segments are also described as being incommensurable, meaning that they share no measure in common, that is, there is no length (the measure), no matter...

Generale di brigata aerea Insegna di grado Aeronautica Militare Istituzione 1923 Esercito Italiano Generale di brigata Marina Militare Contrammiraglio Carabinieri Generale di brigata Grado inferiore:Grado superiore: colonnello Generale di divisione aerea Codice NATO OF-6 Il generale di brigata aerea è il primo, in ordine gerarchico crescente, tra i gradi degli ufficiali generali dell'Aeronautica Militare Italiana. Gerarchicamente, il grado è superiore a quello di colonnello e subalterno a ...
2012 mass shooting in Newtown, Connecticut, US Sandy Hook Elementary School shootingPolice at the scene of the shootingLocation of Sandy Hook Elementary School in Newtown, ConnecticutLocationSandy Hook Elementary School, Sandy Hook, Connecticut, U.S.DateDecember 14, 2012; 11 years ago (December 14, 2012) c. 9:35 – c. 9:40 a.m.[1][2][3] EST (UTC−05:00)TargetStudents and staff at Sandy Hook Elementary SchoolAttack typeMass shooting,...

乔治·丰泰斯Georges Fontès2011年埃罗省议会主席任期1982年3月26日—2015年4月2日 贝济耶市长任期1983年3月18日—1989年3月24日 法国众议院议员任期1986年3月16日—1986年4月1日 法国退伍军人事务国务秘书任期1986年3月20日—1988年5月10日 总统弗朗索瓦·密特朗 个人资料出生1924年9月5日法国贝济耶逝世2020年3月2日(2020歲—03—02)(95歲)法国圣希尼扬国籍 法國政党社会民主党保衛共和�...

Nick Hern BooksFounded1988FounderNick HernCountry of originUnited KingdomHeadquarters locationShepherd's BushLondon, W12United KingdomDistributionGrantham Books Services(UK)Theatre Communications Group (USA)Playwrights Canada Press (Canada)Currency Press (Australia)[1]Publication typesbooks, play-scriptsOfficial websitewww.nickhernbooks.co.uk Nick Hern Books is a London-based independent specialist publisher of plays, theatre books and screenplays. The company was founded by the form...

In this Chinese name, the family name is Hung (洪). Hung HuangBornBeijing, ChinaCitizenshipAmericanAlma materVassar CollegeOccupationMedia figureSpouses Andrew Yu (m. 1983–1985) Chen Kaige (m. 1989–1991) Pon Sai (m. 1993–2005) Yang Xiaoping (m. 2005) Children1 (adopted)Parents Zhang Hanzhi (mother) H...

Lalayecomune Lalaye – Veduta LocalizzazioneStato Francia RegioneGrand Est Dipartimento Basso Reno ArrondissementSélestat-Erstein CantoneMutzig TerritorioCoordinate48°20′N 7°16′E48°20′N, 7°16′E (Lalaye) Altitudine297 e 822 m s.l.m. Superficie8,27 km² Abitanti444[1] (2009) Densità53,69 ab./km² Altre informazioniCod. postale67220 Fuso orarioUTC+1 Codice INSEE67255 CartografiaLalaye Sito istituzionaleModifica dati su Wikidata · Manuale Lal...

Pour les articles homonymes, voir Feuerwerker. Antoinette FeuerwerkerBiographieNaissance 24 novembre 1912Anvers (Borgerhout), BelgiqueDécès 10 février 2003 (à 90 ans)Jérusalem, IsraëlNom de naissance Antoinette GluckNationalité FrançaiseFormation Faculté de droit de l'université de Strasbourg, HEC à StrasbourgActivité JuristeFratrie Salomon GluckRose WarfmanConjoint David FeuerwerkerEnfant Atara MarmorAutres informationsDistinction Chevalier des Palmes académiquesmodifier -...

![{\displaystyle f:[a,b]\rightarrow \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc0d2d0b70573525d149ab82948308455d1853d0)
![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)

![{\displaystyle P=\left\{[x_{0},x_{1}],[x_{1},x_{2}],\dots ,[x_{n-1},x_{n}]\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/096b0a34cf6fae9227f91ca153b55cb9f60e4492)




![{\displaystyle {\overline {x_{i}}}\in [x_{i-1},x_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2eb04e9f9c6be3ca045d12f4a5d324a1fb5e3ee)


![{\displaystyle [x_{i-1},x_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09cb12a889d47020c8ce7046a2eb60785e00c0b6)





![{\displaystyle f({\overline {x_{i}}})=\sup f([x_{i-1},x_{i}])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/210793697a0e80ff2a352aad3c60512ff2ea690e)
![{\displaystyle f({\overline {x_{i}}})=\inf f([x_{i-1},x_{i}])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5cbeccbbca500de064919d8ab5613c6f8d52722)






![{\displaystyle A_{\mathrm {kiri} }=\Delta x\left[f(a)+f(a+\Delta x)+\cdots +f(b-\Delta x)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0acfb89f74fd13815c3ae55244a73d0be3da5819)

![{\displaystyle A_{\mathrm {kanan} }=\Delta x\left[f(a+\Delta x)+f(a+2\,\Delta x)+\cdots +f(b)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da9155a88081cbdbb2e154e1cfaf763cfc9029df)




![{\displaystyle A_{\mathrm {tengah} }=\Delta x\left[f(a+{\tfrac {\Delta x}{2}})+f(a+{\tfrac {3\,\Delta x}{2}})+\cdots +f(b-{\tfrac {\Delta x}{2}})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c8188f1f1942f196804920c7f5f9fffb26bd8f4)





![{\displaystyle A_{\mathrm {trap} }={\tfrac {1}{2}}\,\Delta x\left[f(a)+2f(a+\Delta x)+2f(a+2\,\Delta x)+\cdots +f(b)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f07f5b1bcccbd39b36b8a42d8ecca201676f3bf7)