Identitas Bézout
|
Read other articles:

Logo Earth Hour. Earth Hour adalah sebuah kegiatan global yang diadakan oleh World Wide Fund for Nature (WWF) pada Sabtu terakhir bulan Maret setiap tahunnya. Kegiatan ini berupa pemadaman lampu yang tidak diperlukan di rumah dan perkantoran selama satu jam untuk meningkatkan kesadaran akan perlunya tindakan serius menghadapi perubahan iklim. Kegiatan yang dicetuskan WWF dan Leo Burnett ini pertama kali diselenggarakan pada tahun 2007. Saat itu, 2,2 juta penduduk Sydney berpartisipasi dengan ...

Home of the Dwarves in Norse Mythology This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Niðavellir – news · newspapers · books · scholar · JSTOR (June 2015) (Learn how and when to remove this template message) In Norse cosmology, Niðavellir (anglic. as Nidavellir; probable compound of O.N. Nið – new moon...

American politician John Plank TraceyMember of the U.S. House of Representativesfrom Missouri's 7th districtIn officeMarch 4, 1895 – March 3, 1897Preceded byJohn T. HeardSucceeded byJames Cooney Personal detailsBorn(1836-09-18)September 18, 1836Wayne County, OhioDiedJuly 24, 1910(1910-07-24) (aged 73)Springfield, MissouriPolitical partyRepublicanProfessionlawyer John Plank Tracey (September 18, 1836 – July 24, 1910) was a U.S. Representative from Missouri. Born i...

Bengali poet, writer, and editor (1887–1923) Sukumar RayBorn(1887-10-30)30 October 1887Calcutta, Bengal Presidency, British India[1][2]Died10 September 1923(1923-09-10) (aged 35)Calcutta, Bengal Presidency, British IndiaOccupationWriter, poet, editorLanguageBengaliAlma materPresidency University, KolkataLondon College of CommunicationPeriodBengal RenaissanceNotable worksAbol Tabol, Pagla Dashu, HaJaBaRaLaSpouseSuprabha DeviChildrenSatyajit Ray (son)ParentsUpendraki...

Curtis Good Informasi pribadiNama lengkap Curtis Edward GoodTanggal lahir 23 Maret 1993 (umur 31)Tempat lahir Melbourne, AustraliaTinggi 1,87 m (6 ft 1+1⁄2 in)Posisi bermain BekInformasi klubKlub saat ini Newcastle UnitedNomor 33Karier junior Box Hill United2005—2008 Nunawading City2009 VIS2009—2010 AISKarier senior*Tahun Tim Tampil (Gol)2011–2012 Melbourne Heart 25 (1)2012– Newcastle United 0 (0)2012–2013 → Bradford City (pinjaman) 3 (0)2014 → Dundee ...

Association football tournament in England 1966 FIFA World CupTournament detailsHost countryEnglandDates11–30 JulyTeams16 (from 4 confederations)Venue(s)8 (in 7 host cities)Final positionsChampions England (1st title)Runners-up West GermanyThird place PortugalFourth place Soviet UnionTournament statisticsMatches played32Goals scored89 (2.78 per match)Attendance1,563,135 (48,848 per match)Top scorer(s) Eusébio (9 goals)← 1962 1970 → I...

Detail of the Wellington Monument This is a list of public art in Hyde Park, London. A Royal Park since 1536, Hyde Park covers an area of over 350 acres.[1] Its present landscaping dates largely to the 18th century, when Queen Caroline introduced the Serpentine among other features, and to the 1820s, when Decimus Burton made improvements including the park's triumphal entrance at Wellington Arch.[2] In the immediate vicinity of the arch, at Hyde Park Corner, there is a signif...

American journalist and news anchor This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Fredricka Whitfield – news · newspapers · books · scholar · JSTOR (July 2014) (Learn how and when to remove th...

Robot used in manufacturing This article is about manufacturing robots. For mining robots, see Automated mining. Part of a series onAutomation Automation in general Banking Building Home Highway system Laboratory Library Broadcast Mix Pool cleaner Pop music Reasoning Semi-automation Telephone Attendant Switchboard Teller machine Vehicular Vending machine Robotics and robots Domestic Vacuum cleaner Roomba Lawn mower Guided vehicle Industrial Paint ODD Impact of automation Manumation OOL Bias S...

Terusan NikaraguaSpesifikasi teknisStatusSedang dibangunSejarahTanggal pengesahan2013 Terusan Nikaragua (bahasa Spanyol: Canal de Nicaragua), resminya Nicaraguan Canal and Development Project (disebut juga Terusan Besar Nikaragua atau Terusan Besar Antarlautan Nikaragua) adalah rute perkapalan yang sedang dibangun melintasi Nikaragua supaya menghubungkan Laut Karibia (sekaligus Samudra Atlantik) dengan Samudra Pasifik. Pada Juni 2013, Majelis Nasional Nikaragua menyetujui RUU yang memberi...

American alternative rock duo This article is about the American rock band. For other uses, see The Score (disambiguation). This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: The Score band – news · newspapers ·...

一中同表,是台灣处理海峡两岸关系问题的一种主張,認為中华人民共和国與中華民國皆是“整個中國”的一部份,二者因為兩岸現狀,在各自领域有完整的管辖权,互不隶属,同时主張,二者合作便可以搁置对“整个中國”的主权的争议,共同承認雙方皆是中國的一部份,在此基礎上走向終極統一。最早是在2004年由台灣大學政治学教授張亞中所提出,希望兩岸由一中各表�...

Lambang kotamadya Finnøy ialah sebuah kotamadya di provinsi Rogaland, Norwegia, yang merupakan kotamadya pulau yang terletak di Boknafjorden, 13 mil laut (24 km) utara Stavanger. Sering dinyatakan bahwa matematikawan Norwegia Niels Henrik Abel (1802-1829) lahir di Finnøy, karena ayahnya Søren Georg bertindak sebagai rektor di sini. Namun studi-studi terkini mengindikasikan bahwa ia lahir di Nedstrand, sebuah paroki di dekatnya. Finnøy berada di puncak kekuasaanya pada pertengahan aba...

1864–65 United States Senate elections ← 1862 & 1863 Various dates 1866 & 1867 → 24 of the 72 seats in the United States Senate (with special elections)25 seats needed for a majority Majority party Minority party Leader Henry B. Anthony[a] Party Republican Democratic Leader since March 4, 1863 Leader's seat Rhode Island Last election 32 seats 10 seats Seats before 31 10 Seats after 33 9 Seat change 2 1 Seats ...

Mustapha Hadji Hadji pada tahun 2012Informasi pribadiTanggal lahir 16 November 1971 (umur 52)Tempat lahir Ifrane Atlas-Saghir, MarokoPosisi bermain GelandangKarier senior*Tahun Tim Tampil (Gol)1991–1996 Nancy 243 (98)1996–1997 Sporting CP 27 (3)1997–1999 Deportivo la Coruña 31 (2)1999–2001 Coventry City 62 (12)2001–2004 Aston Villa 35 (2)2004 Espanyol 16 (1)2004–2005 Emirates Club 15 (5)2005–2007 1. FC Saarbrücken 54 (10)2007–2010 Fola Esch 44 (25)Total 518 (155)Tim na...

American author, columnist, and political commentator Mollie HemingwayHemingway in 2016BornMollie Ziegler (1974-08-03) August 3, 1974 (age 49)Denver, Colorado, U.S.Alma materUniversity of Colorado DenverOccupation(s)Author, columnist, political commentatorSpouse Mark Hemingway (m. 2006) Mollie Ziegler Hemingway (born August 3, 1974) is an American conservative author, columnist, and political commentator.[1][2] She is the editor in chie...

Land warfare branch of Denmark's military Royal Danish ArmyHærenCoat of arms of the Royal Danish ArmyFounded17 November 1614; 409 years ago (1614-11-17)[1]Country Kingdom of DenmarkAllegiance Frederik X Denmark Faroe Islands GreenlandTypeArmyRoleLand warfareSizeActive: 25,400[2]Reserve: 63,000 363 tracked and 257 wheeled armoured vehicles[3]Part ofDanish Armed ForcesEquipmentSee listEngagementsThirty Years' War (1625–1629)T...

Irish-born American military officer and politician Edward HandBorn(1744-12-31)31 December 1744Clyduff, King's County, IrelandDied3 September 1802(1802-09-03) (aged 57)Rock Ford, Lancaster, PennsylvaniaBuriedSt. James's Episcopal Cemetery Lancaster, PennsylvaniaAllegiance United Kingdom of Great Britain United StatesService/branch British Army Continental ArmyRankMajor GeneralUnitRoyal Irish RegimentCommands held1st Pennsylvania RegimentBattles/warsSiege of Yorktown Edward Hand (31 ...
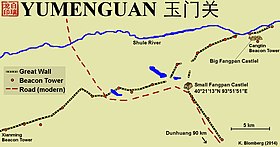
Lintasan YumenReruntuhan Kastel Fangpa Kecil di Lintasan YumenLokasi80 km barat laut Dunhuang, Gansu, TiongkokKoordinat40°21′12.6″N 93°51′50.5″E / 40.353500°N 93.864028°E / 40.353500; 93.864028 Peta tentang Lintasan Yumen Kastel Fangpa Kecil di Lintasan Yumen - pintu masuk dari utara Tembok Besar Tiongkok dari Dinasti Han di Lintasan Yumen Lintasan Yumen atau Yumenguan (Hanzi sederhana: 玉门关; Hanzi tradisional: 玉門關; Pinyin: Yùmén Gu...

زوران فيليبوفيتش معلومات شخصية الميلاد 6 فبراير 1953 (العمر 71 سنة)بودغوريتسا، جمهورية يوغوسلافيا الاشتراكية الاتحادية الطول 1.83 م (6 قدم 0 بوصة) مركز اللعب مهاجم الجنسية مونتينيغري معلومات النادي النادي الحالي منتخب صربيا لكرة القدم مسيرة الشباب سنوات فريق 1967–1970 ...


























![{\textstyle {\frac {18}{42/6}}\in [2,3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8519bf3ca74cfeb93f483852dd986533af8f7c0a)






























