37 (angka)

37 adalah bilangan prima takberaturan [en] pertama..^[2]
Jumlah kuadrat 37 bilangan prima pertama habis dibagi oleh 37.^[3]
37 adalah nilai median faktor prima kedua suatu bilangan bulat.^[4]
Setiap bilangan bulat positif adalah jumlah paling banyak 37 pangkat lima (lihat Masalah Waring [en]).^[5]
37 adalah bilangan prima kuban [en] ketiga setelah 7 dan 19..^[6]
37 adalah bilangan prima Padovan [en] kelima, setelah empat bilangan prima pertama 2, 3, 5, dan 7.^[7]
37 juga merupakan bilangan prima keberuntungan [en] kelima, setelah 3, 7, 13, dan 31.^[8]
37 adalah bilangan bintang [en] ketiga^[9] dan bilangan heksagonal tengah [en] keempat.^[10]

Terdapat tepat 37 grup refleksi kompleks [en].

Persegi ajaib terkecil, hanya menggunakan bilangan-bilangan prima dan 1, berisi 37 sebagai nilai dari sel bagian tengahnya:^[11]

31	73	7
13	37	61
67	1	43

Dalam Sains

Nomor atom Rubidium.
Temperatur normal tubuh manusia dalam Celcius.

Astronomi

NGC 2169 [en] dikenal sebagai Cluster 37, karena kemiripannya dengan angka tersebut.

Referensi

^ Sloane, N.J.A. (ed.). "Sequence A007510 (Single (or isolated or non-twin) primes: Primes p such that neither p-2 nor p+2 is prime.)". On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Diakses tanggal 2022-12-05.
^ "Sloane's A000928: Irregular primes". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Diakses tanggal 2016-05-31.
^ Sloane, N.J.A. (ed.). "Sequence A111441 (Numbers k such that the sum of the squares of the first k primes is divisible by k)". On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Diakses tanggal 2022-06-02.
^ Koninck, Jean-Marie de; Koninck, Jean-Marie de (2009). Those fascinating numbers. Providence, R.I: American Mathematical Society. ISBN 978-0-8218-4807-4.
^ Weisstein, Eric W. "Waring's Problem". mathworld.wolfram.com (dalam bahasa Inggris). Diakses tanggal 2020-08-21.
^ "Sloane's A002407: Cuban primes". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Diakses tanggal 2016-05-31.
^ "Sloane's A000931: Padovan sequence". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Diakses tanggal 2016-05-31.
^ "Sloane's A031157: Numbers that are both lucky and prime". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Diakses tanggal 2016-05-31.
^ "Sloane's A003154: Centered 12-gonal numbers. Also star numbers". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Diakses tanggal 2016-05-31.
^ "Sloane's A003215: Hex (or centered hexagonal) numbers". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Diakses tanggal 2016-05-31.
^ Henry E. Dudeney (1917). Amusements in Mathematics (PDF). London: Thomas Nelson & Sons, Ltd. hlm. 125. ISBN 978-1153585316. OCLC 645667320. Diarsipkan dari versi asli (PDF) tanggal 2023-02-01.

Pranala luar

Wikimedia Commons memiliki media mengenai 37 (number).

37 Heaven Banyak kumpulan fakta dan pranala tentang bilangan ini.

Artikel bertopik angka ini adalah sebuah rintisan. Anda dapat membantu Wikipedia dengan mengembangkannya.

Read other articles:

Daerah Västra Götaland

Västra Götaland Västra Götalands länDaerah di Swedia Lambang kebesaran CountrySwediaIbu kotaGothenburgPemerintahan • GubernurLars Bäckström • DewanVästra Götaland Regional DewanLuas • Total23.945 km2 (9,245 sq mi)Populasi (March 31 2011)[1] • Total1.589.016 • Kepadatan66/km2 (170/sq mi)Zona waktuUTC+1 (CET) • Musim panas (DST)UTC+2 (CEST)GDP/ NominalSEK 386,538 million (2004)...

Агрегатное состояние

Эта статья содержит материал неэнциклопедичного характера. Пожалуйста, улучшите её в соответствии с правилами написания статей. Агрега́тное состоя́ние вещества (от лат. aggrego «присоединяю») — физическое состояние вещества, зависящее от соответствующего сочетания ...

كلية ستانيسلاس في باريس

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (يوليو 2020) كلية ستانيسلاس في باريس معلومات التأسيس 1804 الموقع الجغرافي إحداثيات 48°50′41�...

Malayness

Socio-political term Sultan Omar Ali Saifuddin Mosque in Brunei on the eve of Ramadhan. The wealthy kingdom adopted Melayu Islam Beraja (Malay Islamic Monarchy) as the national philosophy since its independence in 1984. Malayness (Malay: Kemelayuan, Jawi: كملايوان‎) is the state of being Malay or of embodying Malay characteristics. This may include that which binds and distinguishes the Malay people and forms the basis of their unity and identity. People who call themselves Mala...

Синелобый амазон

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

Felony murder rule

Legal doctrine in some common-law jurisdictions Felony murder redirects here. For the general felony of murder in some jurisdictions, see Murder. Not to be confused with Malice murder. Part of a series onHomicide Murder Note: Varies by jurisdiction Assassination Child murder Consensual homicide Contract killing Crime of passion Depraved-heart murder Felony murder rule Foeticide Honor killing Human cannibalism Child cannibalism Human sacrifice Child sacrifice Internet homicide Lonely hearts ki...

Jeonbuk Hyundai Motors

Jeonbuk Hyundai Motors전북 현대 모터스 FCNama lengkapJeonbuk Hyundai Motors Football Club전북 현대 모터스 축구단JulukanGreens Warriors (녹색 전사) (Pasukan Hijau}Berdiri1994 ,sebagai Jeonbuk DinosStadionJeonju World Cup Stadium(Jeonju Castle)(Kapasitas: 43,348)PemilikHyundai Motor CompanyKetuaChung Mong-KooManajerFabio LefundesLigaK-League2022ke-2Situs webSitus web resmi klub Kostum kandang Kostum tandang Jeonbuk Hyundai MotorsHangul전북 현대 모터스 Hanja全�...

Humanists International

Humanists InternationalHistoireFondation 1952CadreForme juridique Charitable incorporated organisationSiège Londres (EC1V 8BB)États-UnisPays Royaume-UniOrganisationChiffre d'affaires 562 350 € (2020)Site web (en) humanists.internationalIdentifiantsIRS 52-2194803Companies House FC020642modifier - modifier le code - modifier Wikidata Humanists International, appelé jusqu'en 2019 Union internationale humaniste et éthique (en anglais International Humanist and Ethical Union,...

Michal Rozin

Michal RozinLahir25 Juni 1969 (umur 54)Tempat lahirRamat Gan, IsraelKnesset19, 20, 21Faksi yang diwakili di Knesset2013–2019Meretz Michal Rozin (Ibrani: מִיכַל רוֹזִין, lahir 25 Juni 1969) adalah seorang politikus asal Israel. Ia menjabat sebagai anggota Knesset dari partai Meretz. Referensi Pranala luar Wikimedia Commons memiliki media mengenai Michal Rozin. Michal Rozin di situs web Knesset Michal Rozin Diarsipkan 2016-11-11 di Wayback Machine. on the Meretz website Peng...

Selah (biblical figure)

Ancestor of Abraham according to Genesis in Hebrew Bible This article uses texts from within a religion or faith system without referring to secondary sources that critically analyze them. Please help improve this article. (February 2020) (Learn how and when to remove this message) SelahPortrait from Promptuarii Iconum Insigniorum (1553)Born1691 AMDied2124 AM (aged 433)ChildrenEber, and other sons and daughtersParentArpachshad (or Cainan) Selah (Hebrew: שֶׁלַח, romanized: Šélaḥ...

Élections au Danemark

Résultats des élections en 2015. Le Danemark est une monarchie constitutionnelle à régime parlementaire. Quatre types d'élections ont lieu au Danemark : les élections européennes ; les élections législatives ; les élections régionales ; les élections municipales. Élections européennes Modalités du scrutin Les élections européennes sont les élections des députés au Parlement européen. Elles sont régies par l'article 14 du Traité sur l'Union européenn...

2016年美國總統選舉

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人唐納·川普希拉莉·克林頓政党共和黨民主党家鄉州紐約州紐約州竞选搭档迈克·彭斯蒂姆·凱恩选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

Rizal Park

Cet article est une ébauche concernant les Philippines. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (avril 2020). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article...

Rififi in Tokyo

1963 film Rififi in TokyoDirected byJacques DerayWritten byAuguste Le Breton (novel) José Giovanni Jacques Deray Rodolphe-Maurice Arlaud José GiovanniProduced byJacques Bar Luigi NanneriniStarringKarlheinz Böhm Charles Vanel Barbara LassCinematographyTadashi AramakiEdited byAlbert JurgensonMusic byGeorges DelerueProductioncompaniesCompagnia Cinematografica Mondiale Compagnie Internationale de Productions CinématographiquesDistributed byMetro-Goldwyn-MayerRelease date March 29, 1...

The Taking of Tiger Mountain

2014 Chinese-Hong Kong epic action film by Tsui Hark Not to be confused with Taking Tiger Mountain by Strategy (film) or Taking Tiger Mountain (film). For other uses, see Taking Tiger Mountain (disambiguation). The Taking of Tiger MountainTheatrical release posterDirected byTsui HarkScreenplay by Huang Xin Li Yang Tsui Hark Wu Bing Dong Zhe Lin Chi-an Based onTracks in the Snowy Forestby Qu BoProduced by Huang Jianxin Shi Nansun Yu Dong Starring Zhang Hanyu Tony Leung Ka-fai Lin Gengxin Yu Na...

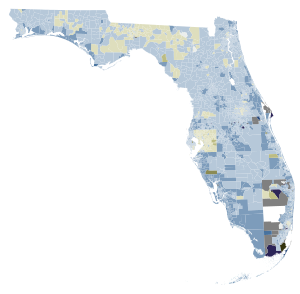
2022 Florida Amendment 1

Proposed amendment to the Florida Constitution 2022 Florida Amendment 1Limitation on the assessment of real property used for residential purposes.Results Choice Votes % Yes 4,016,022 57.26% No 2,997,158 42.74% Valid votes 7,013,180 100.00% Invalid or blank votes 0 0.00% Total votes 7,013,180 100.00% County results Precinct results Yes 90–100% 80–90% 70–80% 60–70% 50–60% No 90–100% 80–90% &...

Soviet Central Asia

Section of Central Asia formerly controlled by the Soviet Union For the geographical subregion in general, see Central Asia. Soviet Central AsiaArea4,003,451 km2 (1,545,741 sq mi)DemonymCentral Asian, SovietCountries Soviet Union 5 Republics Kazakhstan Kyrgyzstan Tajikistan Turkmenistan Uzbekistan LanguagesKarakalpak, Kazakh, Kyrgyz, Russian, Tajik, Turkmen, Uzbek, and OthersTime zones 2 time zones UTC+05:00: Standard: Kazakhstan (5 regions), Tajikistan, Turkmenistan, Uzbe...

Harry Potter and the Goblet of Fire (film)

2005 film by Mike Newell Harry Potter and the Goblet of FireTheatrical release posterDirected byMike NewellScreenplay bySteve KlovesBased onHarry Potter and the Goblet of Fireby J. K. RowlingProduced byDavid HeymanStarring Daniel Radcliffe Rupert Grint Emma Watson Robbie Coltrane Ralph Fiennes Michael Gambon Brendan Gleeson Jason Isaacs Gary Oldman Alan Rickman Maggie Smith Timothy Spall CinematographyRoger PrattEdited byMick AudsleyMusic byPatrick DoyleProductioncompanies Warner Bros. Pictur...

2020 United States House of Representatives elections in North Carolina

Not to be confused with 2020 North Carolina House of Representatives election. 2020 United States House of Representatives elections in North Carolina ← 2018 November 3, 2020 2022 → All 13 North Carolina seats to the United States House of Representatives Majority party Minority party Party Republican Democratic Last election 10 3 Seats won 8 5 Seat change 2 2 Popular vote 2,631,336 2,660,535 Percentage 49.4% 50.0% Swing 0.98% 1.61% Rep...

كايل سينجلير

كايل سينجلير معلومات شخصية الميلاد 4 مايو 1988 (العمر 36 سنة)ميدفورد الطول 6 قدم 8 بوصة (2.0 م) مركز اللعب لاعب هجوم صغير الجسم، ومدافع مسدد الهدف الجنسية الولايات المتحدة الوزن 104 كيلوغرام[1] المدرسة الأم جامعة ديوك[2] الحياة العملية الفرق أوكلاهوم...