音高
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Donabate (bahasa Irlandia: Domhnach Bat) ialah sebuah kota di County Fingal, Republik Irlandia. Donabate adalah bagian pinggiran Dublin, terletak 25 km dari ibu kota Irlandia tersebut. Kota ini didirikan di atas sebuah semenanjung kecil di Laut Irlandia, yang dibagi bersama kota Portrane. Asal nama kota ini berubah-ubah sepanjang waktu; Donabate kadang-kadang dieja « Donaghbate » Kota Donabate berpenduduk 5.713 jiwa (2006). Pada tahun 1912 dilaporkan terdapat penduduk sebaya...

Слепая подпись (англ. blind signature) — разновидность ЭЦП, особенностью которой является то, что подписывающая сторона не может точно знать содержимое подписываемого документа. Понятие слепой подписи придумано Дэвидом Чаумом[1] в 1982 году, им же предложена первая реал�...

Jambu biji getas merah Klasifikasi ilmiah Kerajaan: Plantae (tanpa takson): Angiospermae (tanpa takson): Eudikotils (tanpa takson): Rosids Ordo: Myrtales Famili: Myrtaceae Subfamili: Myrtoideae Tribus: Myrteae Genus: Psidium Jambu biji getas merah adalah varian jambu biji yang berdaging hijau sampai kekuning-kuningan dan berisi merah muda. Jambu ini beda dengan jambu pasar minggu, jambu ini bentuknya agak melonjong dan rasanya kurang manis, tetapi jambu ini memiliki khasiat yang baik karena ...

State general election for Western Australia, held on 13 March 2021 2021 Western Australian state election ← 2017 13 March 2021 2025 → ← outgoing memberselected members →All 59 seats in the Western Australian Legislative Assembly and all 36 members in the Western Australian Legislative Council30 Assembly seats are needed for a majorityOpinion pollsTurnout1,467,159 (85.46%) First party Second party Third party Leader Mark McGowan M...

American actor Lee PacePace in September 2019 at Paris Fashion WeekBornLee Grinner Pace (1979-03-25) March 25, 1979 (age 45)Chickasha, Oklahoma, U.S.[1]EducationJuilliard School (BFA)OccupationActorYears active2001–presentSpouseMatthew Foley Lee Grinner Pace[2] (born March 25, 1979)[3] is an American actor. He is known for starring as Thranduil the Elvenking in The Hobbit trilogy and as Joe MacMillan in the period drama television series Halt and Catch Fire...

Bernabò Visconti[1] Bernabò Visconti (juga disebut Barnabò) (1323 – 18 Desember 1385) merupakan seorang prajurit dan negarawan berkebangsaan Italia, yang merupakan Raja Milan. Kehidupan Ia dilahirkan di Milan, putra Stefano Visconti dan Valentina Doria. Dari tahun 1346 s/d tahun 1349 ia tinggal di pengasingan, sampai ia dipanggil pulang oleh pamannya Giovanni Visconti. Pada tanggal 27 September 1350 Bernabò menikahi Beatrice Regina della Scala, putri Mastino II, Raja Verona dan ...

Public school in Texas, United States This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: North Side High School Fort Worth, Texas – news · newspapers · books · scholar · JSTOR (April 2022) (Learn how and when to remove this template message) North Side High SchoolLocation2211 Mckinley AvenueFort Worth, Tex...

Chromium(III) iodide Names IUPAC name Chromium(III) iodide Other names Chromium triiodide, chromic iodide Identifiers CAS Number 13569-75-0 3D model (JSmol) Interactive image ChemSpider 75416 ECHA InfoCard 100.033.614 EC Number 236-991-3 PubChem CID 83586 CompTox Dashboard (EPA) DTXSID50929111 InChI InChI=1S/Cr.3HI/h;3*1H/q+3;;;/p-3Key: PPUZYFWVBLIDMP-UHFFFAOYSA-KInChI=1/Cr.3HI/h;3*1H/q+3;;;/p-3/rCrI3/c2-1(3)4Key: PPUZYFWVBLIDMP-GXOYXQMQAU SMILES [Cr](I)(I)I Properties Chemical for...

Hinokitiol[1] Names Preferred IUPAC name 2-Hydroxy-6-(propan-2-yl)cyclohepta-2,4,6-trien-1-one Other names β-Thujaplicin; 4-Isopropyltropolone Identifiers CAS Number 499-44-5 Y 3D model (JSmol) Interactive image ChEBI CHEBI:10447 N ChEMBL ChEMBL48310 Y ChemSpider 3485 Y ECHA InfoCard 100.007.165 KEGG D04876 Y PubChem CID 3611 UNII U5335D6EBI Y CompTox Dashboard (EPA) DTXSID6043911 InChI InChI=1S/C10H12O2/c1-7(2)8-4-3-5-9(11)10(12)6-8/h3-7H,1-2H3,(H,11,1...

Disambiguazione – Se stai cercando altri significati, vedi Ritratto (disambigua). Questa voce o sezione sull'argomento arte è priva o carente di note e riferimenti bibliografici puntuali. Commento: Le poche note sono tutte esplicative. Una voce così importante merita una fontazione più accurata. Sebbene vi siano una bibliografia e/o dei collegamenti esterni, manca la contestualizzazione delle fonti con note a piè di pagina o altri riferimenti precisi che indichino puntualmente la ...

A state private university in Lucknow, Uttar Pradesh, India. For the learning community based on Ken Wilber's integral theory, see Integral Institute. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Integral University – news · newspapers · books · scholar · JSTOR (December 2011) (Learn how and when to remov...
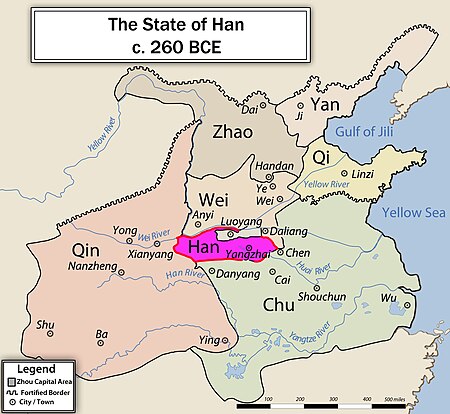
Han韓 or 韩*[g]ˤar403 SM–230 SMStatusKerajaanIbu kotaYangzhai (sebelum 375 SM)Xinzheng (setelah 375 SM)Agama Agama tradisional TiongkokPemujaan nenek moyangPemerintahanMonarkiRaja Kanselir Era SejarahPeriode Negara Perang• Pembagian Jin 403 SM• Ditaklukan oleh Qin 230 SM Mata uangUang sekopKoin tradisional Tiongkok lainnya Didahului oleh Digantikan oleh Jin (negara Tiongkok) dnsDinasti Qin Sunting kotak info • Lihat • BicaraBant...

2023 television film by Anya Adams Prom PactOfficial release posterGenreRomantic comedyWritten byAnthony LombardoDirected byAnya AdamsStarring Peyton Elizabeth Lee Milo Manheim Blake Draper Monique Green Arica Himmel Jason Sakaki David S. Jung Wendi McLendon-Covey Margaret Cho Country of originUnited StatesOriginal languageEnglishProductionExecutive producers Julie Bowen Melvin Mar Jake Kasdan Rachael Field Anya Adams Running time98 minutesProduction companies Bowen and Sons The Detective Age...

Professor at Selçuk University This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article is an orphan, as no other articles link to it. Please introduce links to this page from related articles; try the Find link tool for suggestions. (July 2016) This article may need to be rewritten to comply with Wikipedia's quality standards. You can help. The talk page may contain suggestions. (Ma...

International athletics championship event2007 German Athletics ChampionshipsDates21–22 July 2007Host cityErfurt, GermanyVenueSteigerwaldstadionRecords set1 Championship Record← 2006 Ulm 2008 Nuremberg → The 2007 German Athletics Championships were held at the Steigerwaldstadion in Erfurt on 21–22 July 2007. Results Men Gold Silver Bronze 100 m (+0.3 m/s) Alexander Kosenkow 10.35 Ronny Ostwald 10.37 Marius Broening 10.41 200 m (−0.7 m/s) Daniel Schnelting 20.88 Alexander Kos...

Public college in Purchase, New York, U.S. State University of New York at PurchaseMottoThink Wide OpenTypePublic liberal arts collegeEstablished1967; 57 years ago (1967)Parent institutionState University of New YorkEndowment$77.9 million (2019)[1]PresidentMilagros “Milly” Peña[2]ProvostEarnest Lamb[3]Academic staff300[4]Students3,695[5][6]Undergraduates3,610Postgraduates85LocationPurchase, New York, United States41°02′...

Radio station in Texarkana, ArkansasKOSYTexarkana, ArkansasBroadcast areaTexarkanaFrequency790 kHzProgrammingFormatDefunct (formerly oldies)AffiliationsWestwood OneOwnershipOwnerTownsquare Media(Townsquare License, LLC)Sister stationsKKYR, KMJI, KPWW, KYGLHistoryFormer call signsKOSY (1951–1989)KKYR (1989–2002)Technical informationFacility ID7072ClassBPower1,000 watts day500 watts nightTransmitter coordinates33°22′30″N 94°1′0″W / 33.37500°N 94.01667°W ...

Aristofanes Nama dalam bahasa asli(grc) Ἀριστοφάνης BiografiKelahirank. 445 SM Athena Kematian385 SM (59/60 tahun)Athena KegiatanSpesialisasiSastra dan drama Pekerjaancomedy writer, penulis drama, penyair GenreComedy AliranKomedi Kuno Dipengaruhi olehPindaros, Euripides dan Socrates Karya kreatifKarya terkenal(392 SM) Assemblywomen(405 SM) Katak-katak(408 SM) Plutus(411 SM) Thesmophoriazusae(412 SM) Lysistrata(414 SM) Burung-burung(421 SM) Peace(422 SM) The Wasps(423 ...

Book by Julius Evola This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Revolt Against the Modern World – news · newspapers · books · scholar · JSTOR (October 2016) (Learn how and when to remove this message) Revolt Against the Modern World First edition English hardcover, published by Inner Traditions in 1995A...

Festival in Ghana by the Ashantis Adae FestivalFlag of Ashanti with the Golden stool symbol at the centerObserved byAshantis in AshantiTypeAncestral worshipDateRepeated nine times per yearFrequencyTwice within 42 days (on a Sunday, Akwasidae, and on a Wednesday, Awukudae) Adae Festival (Twi: resting place) is a celebration in Ashanti. Considered a day of rest, it is the most important ancestral custom of the Ashanti people. Observance Within a six-week cycle, Adae has two celebration day...







![{\displaystyle {\sqrt[{12}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc835f27425fb3140e1f75a5faa35b1e8b9efc35)


