雷沃德 (加利福尼亞州克恩縣)

雷沃德
非建制地區
雷沃德在加利福尼亚州的位置
雷沃德
雷沃德
雷沃德在加利福尼亞州的位置
坐标：35°19′21″N 119°40′45″W / 35.32250°N 119.67917°W / 35.32250; -119.67917
國家美国
州份加利福尼亞州
縣克恩縣
海拔389 公尺（1,276 英尺）
时区太平洋時區（UTC-8）
 • 夏时制PDT（UTC-7）
電話區號661（英语：Area code 661）
地名信息系统ID1661304[1]

雷沃德（英語：Reward）是位於美國加利福尼亞州克恩縣的一個非建制地區。該地的面積和人口皆未知。[2]

地理

雷沃德的座標為35°19′21″N 119°40′45″W / 35.32250°N 119.67917°W / 35.32250; -119.67917[1]，而該地的平均海拔高度為389米（即1276英尺）。

參考文獻

  1. ^ 1.0 1.1 Reward. Geographic Names Information System. United States Geological Survey. 
  2. ^ American FactFinder. 美国人口调查局. [2011-05-14]. （原始内容存档于2013-09-11）. 

Read other articles:

Provinsi Kars

Kars province Kars iliProvince of TurkeyLocation of Kars Province in TurkeyCountryTurkeyRegionEastern AnatoliaLuas • Total9,587 km2 (3,702 sq mi)Populasi (2010-12-31)[1] • Total301.766 • Kepadatan31,000/km2 (82,000/sq mi)Kode area telepon0474Pelat kendaraan36Situs webkars.gov.tr Kars (Turki: Kars ili) adalah sebuah provinsi Turki. Galeri Kars city center Ruins of Ani Atatürk monument in Sarıkamış A ruined bridge in A...

 

Segunda División 2019-2020 (Spagna)

Segunda División 2019-2020Liga Adelante 2019-2020 Competizione Segunda División Sport Calcio Edizione 89ª Organizzatore RFEF Date dal 17 agosto 2019al 23 agosto 2020 Luogo  Spagna Partecipanti 22 Formula Girone all'italiana e play-off Sito web www.lfp.es Risultati Vincitore Huesca(1º titolo) Altre promozioni Cadice Elche Retrocessioni Deportivo La Coruña Numancia Extremadura UD Racing Santander Cronologia della competizione 2018-2019 2020-2021 Manuale La stagione 2019-2020 ...

 

List of Knight's Cross of the Iron Cross recipients (L)

Knight's Cross recipientsAllgradesGrand CrossGolden Oak Leaves, Swordsand DiamondsOak Leaves, Swords and DiamondsOak Leaves and SwordsOakLeaves 1940–41 1942 1943 1944 1945 Foreign Knight'sCross A Ba–Bm Bn–Bz C D E F G Ha–Hm Hn–Hz I J Ka–Km Kn–Kz L M N O P Q R Sa–Schr Schu–Sz T U V W X–Z Foreign  Knight's Cross The Knight's Cross of the Iron Cross (German: Ritterkreuz des Eisernen Kreuzes) and its variants were the highest awards in the military and paramilitary force...

Hell for Sure Lake

Lake in California, United States Hell for Sure LakeAerial image of Hell for Sure Lake [1]Hell for Sure LakeShow map of CaliforniaHell for Sure LakeShow map of the United StatesLocationThe Sierra Nevada of the U.S., within Fresno County, California.Coordinates37°08′19″N 118°48′00″W / 37.1386°N 118.8001°W / 37.1386; -118.8001TypeAlpine lakePart ofRed Mountain Basin[2]Primary outflowsFleming Creek[3]Basin countriesUnited Stat...

 

World Trade Organization Ministerial Conference of 1999

Meeting of the World Trade Organization 1999 Ministerial Conference of the World Trade OrganizationLogoDais of speakers and banners at the Seattle WTO Ministerial ConferenceDate30 November – 3 December 1999 (1999-11-30 – 1999-12-03)LocationSeattle, Washington, USAParticipantsWorld Trade Organization member countriesPrevious eventGeneva WTO Ministerial ConferenceNext event→ Doha WTO Ministerial Conference of 2001 The WTO Ministerial Conference of 1999 was th...

 

Lego Indiana Jones : La Trilogie originale

Cet article est une ébauche concernant le jeu vidéo. Vous pouvez partager vos connaissances en l’améliorant (comment ?) (voir l’aide à la rédaction). Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article contient une ou plusieurs listes (décembre 2018). Ces listes gagneraient à être rédigées sous la forme de paragraphes synthétiques, plus agréables à la lecture, les listes pouvant être aussi introduites par une partie rédigée et...

BBC Radio Cymru

Cet article est une ébauche concernant le pays de Galles. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. BBC Radio Cymru Présentation Pays Pays de Galles Propriétaire BBC Cymru Wales Langue Gallois Site web http://www.bbc.co.uk/radiocymru Historique Création 3 janvier 1977 Diffusion hertzienne Diffusion câble et Internet modifier BBC Radio Cymru est la radio nationale du Pays de Galles en langue galloise. ...

 

Kankakee Torrent

Sandstone cliff at Starved Rock State Park, carved by the force of the Kankakee Torrent some 19,000 years ago The Kankakee Torrent was a catastrophic flood that occurred about 19,000 calibrated years ago[1] in the Midwestern United States. It resulted from a breach of moraines forming a large glacial lake fed by the melting of the Late Wisconsin Laurentide Ice Sheet. The point of origin of the flood was Lake Chicago.[1] The landscape south of Chicago still shows the effe...

 

Japan Academy Film Prize for Outstanding Performance by an Actor in a Leading Role

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Japan Academy Film Prize for Outstanding Performance by an Actor in a Leading Role – news · newspapers · books · scholar · JSTOR (November 2014) (Learn how and when to remove this message) AwardJapan Academy Film Prize for Outstanding Performance by an Actor in a Leading RoleThe...

The Really Really Really Really Boring Album

2019 studio album by Regurgitator's Pogogo Show The Really Really Really Really Boring AlbumStudio album by Regurgitator's Pogogo ShowReleased1 March 2019GenreChildren's musicLength34:59LabelValve Records, ABC MusicProducerRegurgitatorRegurgitator albums chronology Headroxx(2018) The Really Really Really Really Boring Album(2019) Quarter Pounder: 25 Years of Being Consumed(2019) Singles from The Really Really Really Really Boring Album The Pogogo Show ThemeReleased: 26 July 2019[1]...

 

LVTP-5裝甲車

LVTP-5 LVTP-5类型兩棲裝甲運兵車原产地 美国服役记录服役期间1952-参与战争／衝突1958年黎巴嫩危機越戰生产历史研发者博格華納研发日期1950-1951制造数量1124基本规格重量37.4公噸长度9.04公尺宽度3.57公尺高度2.92公尺操作人数3+34 乘員装甲6-16公厘的鋼質裝甲主武器M1919A4機槍(A、A1)、白朗寧M2重機槍(A1與其他款式)、M240通用機槍(LVTH-6)、M49 24倍徑105mm榴彈炮(LVTH-6)、工蜂四型(LVTP-...

 

بوتشو

بوتشو 亳州市    خريطة الموقع تقسيم إداري البلد  الصين[1] التقسيم الأعلى آنهوي (1667–)  خصائص جغرافية إحداثيات 33°51′46″N 115°46′27″E / 33.86264°N 115.77422°E / 33.86264; 115.77422   [2] المساحة 8522.58 كم² الارتفاع 32 السكان التعداد السكاني 4850657 نسمة (إحصاء 2010 census) الكثافة ال...

2015 Wealden District Council election

Election Map of the results The 2015 Wealden District Council election took place on 7 May 2015 to elect members of the Wealden District Council in England.[1] It was held on the same day as other local elections. Results   Conservative: 50 seats   Independent: 5 seats Source:[2] By-elections between 2015 and 2019 Hellingly A by-election was held in Hellingly on 29 October 2015 after the resignation of Conservative councillor Paul Soane, who stood in the by...

 

Ferdinand von Mueller

Ferdinand von MuellerFerdinand von MuellerLahir30 June 1825Rostock, GermanyMeninggal10 October 1896KebangsaanGerman-AustralianWarga negaranoneKarier ilmiahBidangbotany, medicine, geographySingkatan penulis (botani)F.Muell. Ferdinand Jacob Heinrich von Mueller (30 Juni 1825 – 10 Oktober 1896) adalah seorang ahli botani, geografi dan dokter berkebangsaan Jerman-Australia. Ia dilahirkan di Rostock, Jerman dan dibesarkan oleh kakek neneknya setelah kedua orangtuanya meninggal. Ferdinand M...

 

1976 Dutch Grand Prix

1976 Dutch Grand Prix Race 12 of 16 in the 1976 Formula One season← Previous raceNext race → Race detailsDate August 29, 1976Official name XXIII Grote Prijs van Nederland[1]Location Circuit Park ZandvoortZandvoort, NetherlandsCourse Permanent racing facilityCourse length 4.226 km (2.626 miles)Distance 75 laps, 316.960 km (196.950 miles)Weather Warm, dryPole positionDriver Ronnie Peterson March-FordTime 1:21.31[2]Fastest lapDriver Clay Regazzoni FerrariT...

Championnat d'Italie de football 2017-2018

Serie A 2017-2018 Généralités Sport Football Organisateur(s) Federazione Italiana Giuoco Calcio (FIGC) Édition 116e Lieu(x) Italie Date Du 19 août 2017au 20 mai 2018 Participants 20 Matchs joués 380 Affluence 9351260 (24738 par match) Site web officiel Site officiel Hiérarchie Hiérarchie 1re division Niveau inférieur Serie B 2017-2018 Palmarès Tenant du titre Juventus Promu(s) en début de saison Bénévent CalcioHellas VéroneSPAL Vainqueur Juventus (34) Deuxième SSC Naples Trois...

 

認可

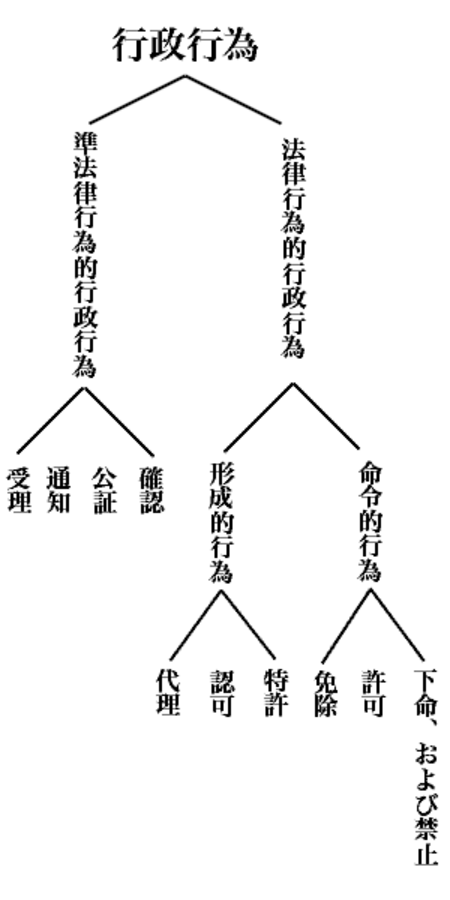
この項目では、法律上の概念について説明しています。セキュリティについては「認可 (セキュリティ)」をご覧ください。 伝統的通説による分類 認可（にんか）とは、行政法学においては行政行為のうち私人の契約、合同行為を補充して法律行為の効力要件とするものをいう（補充行為[1]）[2][3]。 概説 法令が行政庁による是認によって当事者相互の...

 

Ngành Thạch tùng

Ngành Thạch tùngThời điểm hóa thạch: 428–0 triệu năm trước đây TiềnЄ Є O S D C P T J K Pg N Silur[1][2] - gần đâyLycopodiella cernuaPhân loại khoa họcGiới (regnum)PlantaeNgành (divisio)LycopodiophytaCronquist, Takht. & W.Zimm.[3] [P.D. Cantino & M.J. Donoghue][4]Các lớp Lycopodiopsida - thạch tùng Selaginellopsida - quyển bá Isoetopsida - thủy phỉ Zosterophyllopsida † Ngành Thạch tùng hay...

ホワイトハウス

「ホワイトハウス」のその他の用法については「ホワイトハウス (曖昧さ回避)」をご覧ください。 ホワイトハウスWhite House ペンシルベニア大通りに面したレジデンスの正面 ワシントンD.C.の地図を表示アメリカ合衆国の地図を表示情報用途 アメリカ合衆国大統領官邸設計者 ジェームズ・ホーバンチャールズ・フォレン・マッキムベンジャミン・ラトローブネイサン・C�...

 

Fundamental theorem of arithmetic

Integers have unique prime factorizations Not to be confused with Fundamental theorem of algebra or Fundamental theorem of calculus. In Disquisitiones Arithmeticae (1801) Gauss proved the unique factorization theorem [1] and used it to prove the law of quadratic reciprocity.[2] In mathematics, the fundamental theorem of arithmetic, also called the unique factorization theorem and prime factorization theorem, states that every integer greater than 1 can be represented uniquely ...