莫塞萊定律
|
Read other articles:

Brit MarlingBrit Marling di Festival Film Internasional Toronto tahun 2014LahirBrit Heyworth Marling7 Agustus 1982 (umur 41)Chicago, Illinois, Amerika SerikatTempat tinggalLos Angeles, California, Amerika SerikatAlmamaterUniversitas GeorgetownPekerjaanAktris, penulis naskahTahun aktif2007–sekarangDikenal atasI Origins, Another Earth, The East, The OA Brit Heyworth Marling (lahir 7 Agustus 1982) merupakan seorang aktris dan penulis Amerika Serikat. Ia terkenal setelah membintangi ...

2012 film by Scott Derrickson SinisterTheatrical release posterDirected byScott DerricksonWritten by C. Robert Cargill Scott Derrickson Produced by Jason Blum Brian Kavanaugh-Jones Starring Ethan Hawke Juliet Rylance Fred Thompson James Ransone Clare Foley Michael Hall D'Addario CinematographyChristopher NorrEdited byFrédéric ThoravalMusic byChristopher YoungProductioncompanies Summit Entertainment Alliance Films Automatik Entertainment Blumhouse Productions IM Global Alliance Films UK Limi...

The Starving GamesPoster rilis teatrikalSutradaraJason FriedbergAaron SeltzerProduserPeter SafranDitulis olehJason FriedbergAaron SeltzerPemeran Maiara Walsh Cody Christian Brant Daugherty Lauren Bowles Diedrich Bader Penata musikTimothy Michael WynnPerusahaanproduksiSafran Company3 in the BoxDistributorKetchup EntertainmentTanggal rilis 08 November 2013 (2013-11-08)[1] Durasi83 menitNegaraAmerika SerikatBahasaInggrisAnggaran$4.5 jutaPendapatankotor$3,889,688[2] The...

Herman TinoInformasi latar belakangLahir5 Desember 1954 (umur 69)Tanjung Karang, Selangor, MalaysiaPekerjaanPenyanyiTahun aktif1980-an Herman Tino (lahir 5 Desember 1954) adalah penyanyi Malaysia yang aktif antara tahun 1982–1986. Penyanyi yang berasal dari Tanjung Karang, Selangor ini memiliki darah keturunan Jawa. Diskografi Album Akibat Putus Cinta Lagu Kupendam Biarpun Parah Akibat Putus Cinta Pelita Dalam Kabus Cinta Tertahan-tahan Ojo Kesandung Kamar Sepi Mengapa Dikenang Mengapa...

Untuk pulau, lihat Pulau Yos Sudarso.Untuk kapal, lihat KRI Yos Sudarso.Untuk halte Koridor 10, lihat Halte Transjakarta Yos Sudarso Kodamar. Yos Sudarso Informasi pribadiLahir(1925-11-24)24 November 1925Salatiga, Jawa TengahMeninggal15 Januari 1962(1962-01-15) (umur 36)Laut Aru, PapuaSuami/istriSiti Kustini (1955-1962)Anak5PekerjaanTNIKarier militerPihakIndonesiaDinas/cabang TNI Angkatan LautMasa dinas1945 - 1962Pangkat Laksamana Muda TNI (Anumerta)SatuanKorps PelautSunting kotak i...

Liga Eropa UEFA 2013–14Juventus Stadium yang menyelenggarakan pertandingan final.Informasi turnamenJadwalpenyelenggaraan4 Juli – 29 Agustus 2013 (babak kualifikasi)19 September 2013 – 14 Mei 2014 (babak utama)Jumlahtim peserta48+8 (babak utama)161+33 (keseluruhan) (dari 53 asosiasi)Hasil turnamenJuara Sevilla (gelar ke-3)Tempat kedua BenficaStatistik turnamenJumlahpertandingan205Jumlah gol475 (2,32 per pertandingan)Jumlahpenonton3.411.208 (16.640 per pertandingan)Pencetak...
Disambiguazione – Hans Andersen rimanda qui. Se stai cercando altri significati, vedi Hans Andersen (disambigua). Andersen fotografato da Thora Hallager nel 1869.[2] Hans Christian[1] Andersen (pronuncia danese [ˈhans ˈkʰʁæsd̥jan ˈɑnɐsn̩] ascoltaⓘ; Odense, 2 aprile 1805 – Copenaghen, 4 agosto 1875) è stato uno scrittore e poeta danese, celebre soprattutto per le sue fiabe. Tra le sue opere più note vi sono La principessa sul pisello (1835), Mignolina...

Cet article est une ébauche concernant un chanteur allemand. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Roger CiceroRoger Cicero en finale du Concours Eurovision de la chanson 2007BiographieNaissance 6 juillet 1970Berlin-OuestDécès 24 mars 2016 (à 45 ans)HambourgSépulture Cimetière d'OhlsdorfNom de naissance Roger Marcel Cicero CiceuNationalité allemandeFormation Amsterdam University of the Arts...

City in Miami-Dade County, Florida City in Florida, United StatesCoral GablesCityCoral Gables (in foreground) in April 2010. Downtown Miami is barely visible in the background. SealNicknames: The City Beautiful, The GablesLocation of Coral Gables in Miami-Dade County, Florida (left) and of Miami-Dade County in Florida (right)U.S. Census Bureau map showing city limitsCoordinates: 25°43′00″N 80°16′20″W / 25.71667°N 80.27222°W / 25.71667; -80.27222Country...

Motivation in human action This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Self-interest – news · newspapers · books · scholar · JSTOR (August 2014) (Learn how and when to remove this message) An appeal to self-interest during World War II Self-interest generally refers to a focus on the needs or desires (in...

American swimmer Wendy BoglioliBoglioli, at post-Olympic press conference in July, 1976, at Monmouth College, West Long Branch NJPersonal informationFull nameWendy Lou Lansbach BoglioliNational teamUnited StatesBorn (1955-03-06) March 6, 1955 (age 69)Merrill, WisconsinHeight5 ft 11 in (1.80 m)Weight141 lb (64 kg)SportSportSwimmingStrokesFreestyle, ButterflyClubCentral Jersey Aquatic ClubCollege teamMonmouth CollegeCoachDick Steadman(Monmouth)Bill Palmer...

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

Andrea ModaNama resmiAndrea Moda FormulaKantor pusatItaliaPendiriAndrea SassettiPembalap terkenalAlex CaffiEnrico BertaggiaRoberto MorenoPerry McCarthySejarah dalam ajang Formula SatuMesinJuddGelar Konstruktor0Gelar Pembalap0Jumlah lomba13Menang0Posisi pole0Putaran tercepat0Lomba pertamaGrand Prix Afrika Selatan 1992Lomba terakhirGrand Prix Italia 1992 Andrea Moda Formula merupakan sebuah tim Formula Satu asal Italia yang didirikan oleh Andrea Sassetti, yang juga merupakan seorang pengusaha p...

مخطوط لكتاب عربي يظهر فيه حساب وقت الخسوف والكسوف خسوف القمر هو ظاهرة فلكية تحدث عندما يحجب ظل الأرض ضوء الشمس المنعكس على القمر في الأوضاع العادية.[1] وتحدث هذه الظاهرة عندما تكون الشمس والأرض والقمر في حالة اقتران كوكبي كامل (فيكون خسوفا كليا) أو تقريبي (فيكون خسوفا جز...

1844 Paris newspaper Not to be confused with the Jewish-American weekly newspaper Forverts (The Forward), or Vorwärts, the main journal of the Social Democratic Party of Germany, or Vorwärts! Vorwärts!, the Nazi-youth song. Vorwärts! front page, 10 June 1844 Vorwärts! (German pronunciation: [ˈfɔʁvɛʁts], Forward!) was a biweekly newspaper published in Paris from January to December 1844.[1][2] The journal was seen as the most radical in contemporary Europe. ...

American musician Matt DennisBackground informationBirth nameMatthew Loveland DennisBorn(1914-02-11)February 11, 1914Seattle, Washington, U.S.DiedJune 21, 2002(2002-06-21) (aged 88)Riverside, CaliforniaGenresPopular musicOccupation(s)Singer, composerInstrument(s)PianoLabelsCapitolMusical artist Matthew Loveland Dennis (February 11, 1914 – June 21, 2002) was an American singer, pianist, band leader, arranger, and writer of music for popular songs. Biography Dennis was born in Seattle, W...

何鏡堂出生1938年4月(86歲) 中國廣東省第一行政督察區東莞縣石龍鎮国籍 中华人民共和国母校華南工學院职业建筑师建筑 西漢南越王博物館 浙江大學紫金港校區 安徽师范大学花津校区 华南师范大学南海校区 中國2010年上海世界博覽會中國館等 项目 侵华日军南京大屠杀遇难同胞纪念馆擴建工程 何鏡堂(1938年4月—),廣東東莞人,中國當代建築師,现任华南理工�...

مسجد تومبول واجهة المسجد تحت الترميم عام 2010 إحداثيات 43°16′10″N 26°54′36″E / 43.26944444°N 26.91°E / 43.26944444; 26.91 [1] معلومات عامة الموقع شومن القرية أو المدينة شومن الدولة بلغاريا سنة التأسيس 1744 تاريخ بدء البناء 1740 - 1744 المواصفات ارتفاع القبة 25 متر التصميم وا�...
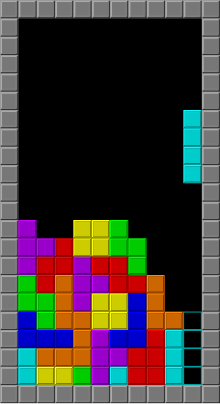
1985 video game This article is about the video game in general. For specific versions, see List of Tetris variants. For other uses, see Tetris (disambiguation). 1985 video gameTetrisA typical Tetris game screenDesigner(s)Alexey PajitnovPlatform(s)List of Tetris variantsReleaseElectronika 60USSR: 1985IBM PCUSSR: 1986EU: November 1987NA: January 1988Genre(s)Puzzletile-matchingMode(s)Single-playermultiplayer Tetris (‹See Tfd›Russian: Тетрис[a]) is a puzzle video game created i...

この項目では、衆議院の小選挙区について説明しています。かつて存在した衆議院の中選挙区については「三重県第1区 (中選挙区)」をご覧ください。 三重県第1区 行政区域 津市、松阪市(2024年1月1日現在)比例区 東海ブロック設置年 1994年(2017年区割変更)選出議員 田村憲久有権者数 355,124人1.566 倍(一票の格差・鳥取1区との比較)(総務省・2023年9月1日)テンプレ...




































