Read other articles:

العلاقات البوتسوانية التشيلية بوتسوانا تشيلي   بوتسوانا   تشيلي تعديل مصدري - تعديل   العلاقات البوتسوانية التشيلية هي العلاقات الثنائية التي تجمع بين بوتسوانا وتشيلي.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه الم...

Leon CzolgoszLeon Czolgosz sekitar tahun 1900, fotografer tidak diketahuiLahirLeon Frank CzolgoszMay 5, 1873[1]Alpena, Michigan, ASMeninggal29 Oktober 1901(1901-10-29) (umur 28)Auburn, New York, ASPekerjaanBuruh bajaGugatan kejahatanFirst-degree murderHukuman kriminalHukuman mati memakai kursi listrikStatus kriminalDieksekusiOrang tuaPaul Czolgosz[2]Mary NowakMotifUntuk memajukan anarkismeAlasanPembunuhan Presiden William McKinley Leon Frank Czolgosz (bentuk Polandia: Cz...

Infection caused by pathogens that take advantage of an opportunity not normally available Medical conditionOpportunistic infectionChest X-ray of a patient who first had influenza and then developed Haemophilus influenzae pneumonia, presumably opportunisticSpecialtyInfectious diseases  An opportunistic infection is an infection caused by pathogens (bacteria, fungi, parasites or viruses) that take advantage of an opportunity not normally available. These opportunities can stem from a vari...

Pervaja Gruppa A 1968 Competizione Vysšaja Liga Sport Calcio Edizione 31ª Organizzatore FFSSSR Date dal 6 aprile 1968al 12 novembre 1968 Luogo  Unione Sovietica Partecipanti 20 Formula Girone all'italiana Risultati Vincitore  Dinamo Kiev(4º titolo) Retrocessioni  Dinamo Kirovobad Statistiche Miglior marcatore Abduraimov Gavasheli (22) Incontri disputati 380 Gol segnati 844 (2,22 per incontro) Cronologia della competizione 1967 1969 Manuale L'edizione 1968 ...

Further information: Khelo India National multi-sport event held in India Khelo India University GamesAbbreviationKIUGFirst event2020, in Bhubaneswar, OdishaOccur everyAnnualPurposeMulti-sport events across Indian universitiesHeadquartersNew DelhiOrganisationsMinistry of Youth Affairs and SportsWebsiteKhelo India University Games Khelo India University Game is a national level multi-sport event held in India, where athletes from universities across the country compete in different sports disc...

Filipino dessert Avocado lamawAlternative namesabukado lamaw, nilamaw nga avocado, avocado milkshake, avocado con leche, milk avocado, avocado puree, avocado shake, avocado smoothie, avocado condensadaCourseDessertPlace of originPhilippinesServing temperatureChilled, room temperatureMain ingredientsAvocado, milk, sugar, ice Avocado and milk in ice (or abukado lamaw) is a traditional Filipino dessert or beverage made from avocado in milk and sugar (condensed milk, evaporated milk, or powdered ...

Malteser InternationalAbbreviationMIFormationJanuary 2, 2005; 19 years ago (2005-01-02)TypeAid agencyPurposeHumanitarian aidDevelopment aidHeadquartersCologne, Germany New York, USRegion served Worldwide(32 countries in 2019)Membership 27 Associations and Priories of the Sovereign Military Order of MaltaOfficial language English, French, GermanSecretary GeneralClemens Graf von Mirbach-HarffPresidentThierry de Beaumont-BeynacAffiliationsSovereign Military Order of MaltaWebsit...

Bilateral relationsFrance-Haiti relations France Haiti Diplomatic missionEmbassy of France, Port-au-PrinceEmbassy of Haiti, Paris France–Haiti relations are foreign relations between France and Haiti. Both nations are members of the Organisation internationale de la Francophonie, United Nations, and the World Trade Organization. History Main article: Saint-Domingue The first French to arrive to Haiti were pirates who began to use the island of Tortuga (northern Haiti) in 1625 as a base and ...

College of the University of Maryland College of Computer, Mathematical, and Natural SciencesTypePublicAffiliationUniversity of Maryland, College ParkDeanAmitabh VarshneyUndergraduates4,912[1]Postgraduates1,424[1]LocationSymons Hall, College Park, Maryland, United StatesNicknameCMNS[2]Websitecmns.umd.edu The College of Computer, Mathematical, and Natural Sciences (CMNS) at the University of Maryland, College Park, is home to ten academic departments[3] and a do...

Corte Suprema de Justicia Palacio de Justicia.LocalizaciónPaís ColombiaInformación generalSigla CSJJurisdicción República de ColombiaTipo Tribunal de JusticiaSede Bogotá ColombiaOrganizaciónPresidente Gerson Chaverra CastroComposición 23 magistradosHistoriaFundación 1886Sitio web oficial[editar datos en Wikidata] La Corte Suprema de Justicia de Colombia es la más alta instancia judicial de la jurisdicción ordinaria en la República de Colombia. La sede está ubicada en el...

1944 film For the earlier film, see The Master Detective (1933 film). The Master DetectiveGerman DVD coverGermanDer Meisterdetektiv Directed byHubert MarischkaWritten byKurt E. WalterFelix von EckardtProduced byFriedrich Wilhelm GaikStarringRudolf PlatteCinematographyOtto BaeckerWalter PindterEdited byMargarete SteinbornMusic byFrank FoxProductioncompanyBerlin-FilmDistributed byDeutsche FilmvertriebsRelease date 10 July 1944 (1944-07-10) Running time74 minutesCountryGermanyLang...

العلاقات اليونانية الكينية اليونان كينيا   اليونان   كينيا تعديل مصدري - تعديل   العلاقات اليونانية الكينية هي العلاقات الثنائية التي تجمع بين اليونان وكينيا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة الي�...

Former building and sculptures from Salonica This article is about the Roman sculptures. For the 1854 novella by Herman Melville, see The Encantadas. Las IncantadasΟι ΜαγεμένεςSide 2 of the columns in the LouvreGeneral informationStatusDemolished (sculptures transferred to the Louvre)Architectural styleCorinthian rhythmTown or cityThessalonikiCountryGreeceFrance (sculptures)Completed2nd century ADDemolished1864Height12,70 m.Technical detailsMaterialMarble Las Incantadas of Salonica...

Not to be confused with Livewell. Type of archaic sail fishing boat Sectional drawing of well smack[1] A well smack was a type of traditional fishing boat in use in the United Kingdom and then the Faroe Islands between the late 18th century and around 1920. It had a well amidships. The well was filled with circulated external water, which kept fish alive until delivered to land and sold. It was a modified form of a fishing smack. History Between roughly 1775 and 1875, well smack refer...

Borough of Remagen, Germany This article needs to be updated. Please help update this article to reflect recent events or newly available information. (September 2010) Rolandseck in 2011 Rolandseck station Rolandseck is a borough in the town of Remagen in Rhineland-Palatinate, Germany. The place consists almost entirely of villas and is a favorite summer resort. Crowning the vine-clad hills behind it lie the ruins of the castle, a picturesque ivy-covered arch, whence a fine view is obtained o...

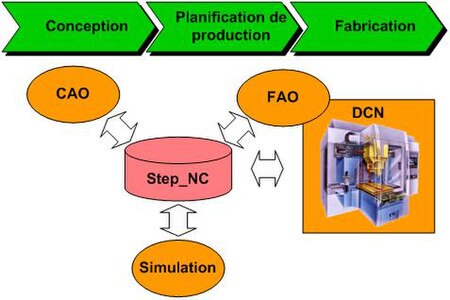
La chaine numérique actuelle simplifiée Le STEP-NC (STEP compliant Numerical Control) est un standard d’échange de données pour la programmation de commande numérique. Il est basé sur le standard STEP (STandard for the Exchange of Product model data, Standard pour l'échange de données de produit) et permet d'intégrer complètement la chaîne numérique CAO-CFAO-CN. Il regroupe à la fois les propriétés du STEP (intégration des processus de conception, de développement, de fabri...

Polynomials arising in knot theory In the mathematical field of knot theory, the HOMFLY polynomial or HOMFLYPT polynomial, sometimes called the generalized Jones polynomial, is a 2-variable knot polynomial, i.e. a knot invariant in the form of a polynomial of variables m and l. A central question in the mathematical theory of knots is whether two knot diagrams represent the same knot. One tool used to answer such questions is a knot polynomial, which is computed from a diagram of the knot and...

Imaging by sections or sectioning using a penetrative wave Not to be confused with Topography. Fig.1: Basic principle of tomography: superposition free tomographic cross sections S1 and S2 compared with the (not tomographic) projected image P Median plane sagittal tomography of the head by magnetic resonance imaging Tomography is imaging by sections or sectioning that uses any kind of penetrating wave. The method is used in radiology, archaeology, biology, atmospheric science, geophysics, oce...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Jiang Wei – berita · surat kabar · buku · cendekiawan · JSTORJiang Wei BiografiKelahiran202 (Kalender Masehi Gregorius) Gangu County (dinasti Han) Kematian3 Maret 264 (61/62 tahun)Chengdu (Cao Wei) Kegia...

Elmo LincolnLincoln pada 1923LahirOtto Elmo Linkenhelt(1889-02-06)6 Februari 1889Rochester, Indiana, Amerika SerikatMeninggal27 Juni 1952(1952-06-27) (umur 63)Los Angeles, California, Amerika SerikatMakamHollywood Forever CemeteryPekerjaanPemeranTahun aktif1913–1952Suami/istriSadie Whited (1913–1921)Ida Lee Tanchick (1935–?) star on Hollywood Walk of Fame (en) Elmo Lincoln (nama lahir Otto Elmo Linkenhelt; 6 Februari 1889 – 27 Juni 1952) adalah seorang pemeran...