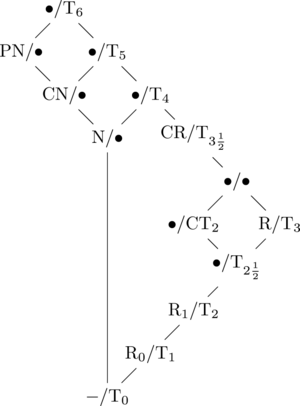
еҲҶзҰ»е…¬зҗҶ
|
Read other articles:

Ereveld Menteng PuloEreveld Menteng PuloDetailsLokasiTebet, JakartaNegaraIndonesiaJenisPemakaman perangPemilikYayasan Pemakaman Perang BelandaLuas29.000 mВІJml. kuburanSekitar 4.300Ereveld Menteng Pulo merupakan sebuah pemakaman bangsa Belanda di Jl. Menteng Pulo RT. 3 RW. 12, Menteng Dalam, Tebet, Jakarta Selatan. Ereveld Menteng Pulo adalah salah satu dari 2 ereveld yang berada di Jakarta selain Ereveld Ancol di Ancol, Pademangan, Jakarta Utara. Permakaman ini dikhususkan bagi perwira milit...

Cult of the Lamb Publikasi11 Agustus 2022GenreRoguelike, aksi-petualangan, simulasi konstruksi dan manajemenLisensiLisensi proprietarium Bahasa Daftar Inggris 60 Karakteristik teknisPlatformWindows, Nintendo Switch, PlayStation 5, Xbox Series X dan S, macOS, PlayStation 4 dan Xbox One MesinUnityModePermainan video pemain tunggal Formatdistribusi digital dan unduhan digital Metode inputpapan tombol komputer, tetikus dan gamepad Format kode Daftar 30 Informasi pengembangPengembangMassive Monste...

Chronologies DonnГ©es clГ©s 1918 1919 1920 1921 1922 1923 1924DГ©cennies :1890 1900 1910 1920 1930 1940 1950SiГЁcles :XVIIIe XIXe XXe XXIe XXIIeMillГ©naires :-Ier Ier IIe IIIe Chronologies gГ©ographiques Afrique Afrique du Sud, AlgГ©rie, Angola, BГ©nin, Botswana, Burkina Faso, Burundi, Cameroun, Cap-Vert, RГ©publique centrafricaine, Comores, RГ©publique du Congo, RГ©publique dГ©mocratique du Congo, CГҙte d'Ivoire, Djibouti, Гүgyp...

Species of cactus Sclerocactus whipplei Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Eudicots Order: Caryophyllales Family: Cactaceae Subfamily: Cactoideae Genus: Sclerocactus Species: S. whipplei Binomial name Sclerocactus whipplei(Engelm. & J.M.Bigelow) Britton & Rose Sclerocactus whipplei, or Whipple's fishhook cactus,[1] is a cactus (family Cactaceae) found in the Colorado Plateau and Canyonlands region of the southwestern ...

NeuroblastomaBentuk tampilan neuroblastoma menggunakan mikroskopInformasi umumSpesialisasiOnkologiPenyebabMutasi Genetik[1]Aspek klinisGejala dan tandaNyeri tulang, pembengkakan[1]Awal munculDibawah usia 5 tahun[1]DiagnosisBiopsi[1]PerawatanObservasi, pembedahan, radiasi, kemoterapi[1]Distribusi dan frekuensiPrevalensi1 diantara 7,000 anak [3]KematianMenyebabkan 15% kematian anak yang disebabkan oleh kanker.[2] Neuroblastoma adalah salah...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Dinesh Chandra Sinha вҖ“ news В· newspapers В· books В· scholar В· JSTOR (March 2022) Dinesh Chandra SinhaаҰҰа§ҖаҰЁа§ҮаҰ¶аҰҡаҰЁа§ҚаҰҰа§ҚаҰ° аҰёаҰҝаҰӮаҰ№Dinesh Chandra SinhaBorn1935Noakhali, Bengal, British IndiaDied16 June 2014Batanagar, Kolkata, IndiaNatio...

Retired American United States Air Force Brigadier General (Special Agent) Richard S. Beyea Jr.Born (1935-09-22) 22 September 1935 (age 88)Atlanta, GeorgiaAllegiance United StatesService/branch United States Air ForceYears of service1958вҖ“1988Rank Brigadier General (Ret.)Commands heldAir Force Office of Special InvestigationsBattles/warsVietnam WarAwards Legion of Merit Meritorious Service Medal Air Force Commendation Medal National Defense Service Medal Vietnam Service Medal ...

2012 NCAA Division I FBS football rankingsSeason2012Bowl season2012вҖ“13 bowl gamesPreseason No. 1USC (AP)LSU (Coaches) End of season championsAlabamaConference with mostteams in final AP pollSEC (7)NCAA Division I FBS football rankings ← 20112013 → Three human polls and one formula ranking make up the 2012 NCAA Division I FBS (Football Bowl Subdivision) football rankings, in addition to various publications' preseason polls. Unlike most sports, college football's gover...

ШалфРөР№ РҫРұСӢРәРҪРҫРІРөРҪРҪСӢР№ РқР°СғСҮРҪР°СҸ РәлаСҒСҒифиРәР°СҶРёСҸ Р”РҫРјРөРҪ:РӯСғРәР°СҖРёРҫСӮСӢРҰР°СҖСҒСӮРІРҫ:Р Р°СҒСӮРөРҪРёСҸРҡлаРҙР°:РҰРІРөСӮРәРҫРІСӢРө СҖР°СҒСӮРөРҪРёСҸРҡлаРҙР°:РӯРІРҙРёРәРҫСӮСӢРҡлаРҙР°:РЎСғРҝРөСҖР°СҒСӮРөСҖРёРҙСӢРҡлаРҙР°:РҗСҒСӮРөСҖРёРҙСӢРҡлаРҙР°:РӣамииРҙСӢРҹРҫСҖСҸРҙРҫРә:РҜСҒРҪРҫСӮРәРҫСҶРІРөСӮРҪСӢРөРЎРөРјРөР№СҒСӮРІРҫ:РҜСҒРҪРҫСӮРәРҫРІСӢРөР РҫРҙ:ШалфРөР№Р’РёРҙ:ШалфРөР№ РҫРұСӢРәРҪРҫРІРөРҪРҪСӢР№ РңРөР¶РҙСғРҪР°СҖРҫРҙРҪРҫРө РҪР°СғСҮРҪРҫРө РҪаз...

American political journalist (born 1976) For the editor of the Century Dictionary and Cyclopedia, see Benjamin Eli Smith. Ben SmithSmith in 2012BornBenjamin Eli Smith (1976-11-04) November 4, 1976 (age 47)New York, New York, U.S.Alma materYale University (BA)OccupationJournalistYears active1999вҖ“presentSpouse Liena Zagare (m. 2002)Children3ParentsRobert S. Smith (father)Dian Golston Smith (mother) Benjamin Eli Smith (born November 4, 1976)[1...

Sceaux иЎҢж”ҝеӣҪ гғ•гғ©гғігӮ№ең°еҹҹеңҸ (RГ©gion) гӮӨгғ«пјқгғүпјқгғ•гғ©гғігӮ№ең°еҹҹеңҸзңҢ (dГ©partement) гӮӘгғјпјқгғүпјқгӮ»гғјгғҢзңҢйғЎ (arrondissement) гӮўгғігғҲгғӢгғјйғЎе°ҸйғЎ (canton) е°ҸйғЎеәҒжүҖеңЁең°INSEEгӮігғјгғү 92071йғөдҫҝз•ӘеҸ· 92330еёӮй•·пјҲд»»жңҹпјү гғ•гӮЈгғӘгғғгғ—гғ»гғӯгғјгғ©гғіпјҲ2008е№ҙ-2014е№ҙпјүиҮӘжІ»дҪ“й–“йҖЈеҗҲ (fr) гғЎгғҲгғӯгғқгғјгғ«гғ»гғҮгғҘгғ»гӮ°гғ©гғігғ»гғ‘гғӘдәәеҸЈеӢ•ж…ӢдәәеҸЈ 19,679дәәпјҲ2007е№ҙпјүдәәеҸЈеҜҶеәҰ 5466дәә/km2дҪҸж°‘гҒ®е‘јз§° ScГ©ensең°зҗҶеә§жЁҷ еҢ—з·Ҝ48еәҰ4...

ЩҮШ°ЩҮ Ш§Щ„Щ…ЩӮШ§Щ„Ш© Ш№ЩҶ Ш§Щ„Щ…Ш¬Щ…ЩҲШ№Ш© Ш§Щ„Ш№ШұЩӮЩҠШ© Ш§Щ„ШЈШӘШұШ§Щғ ЩҲЩ„ЩҠШі Ш№ЩҶ Щ…ЩҶ ЩҠШӯЩ…Щ„ЩҲЩҶ Ш¬ЩҶШіЩҠШ© Ш§Щ„Ш¬Щ…ЩҮЩҲШұЩҠШ© Ш§Щ„ШӘШұЩғЩҠШ© ШЈШӘШұШ§ЩғTГјrkler (ШЁШ§Щ„ШӘШұЩғЩҠШ©) Ш§Щ„ШӘШ№ШҜШ§ШҜ Ш§Щ„ЩғЩ„ЩҠШ§Щ„ШӘШ№ШҜШ§ШҜ 70~83 Щ…Щ„ЩҠЩҲЩҶ ЩҶШіЩ…Ш©Щ…ЩҶШ§Ш·ЩӮ Ш§Щ„ЩҲШ¬ЩҲШҜ Ш§Щ„Щ…Щ…ЩҠШІШ©Ш§Щ„ШЁЩ„ШҜ Ш§Щ„ЩӮШ§ШҰЩ…Ш© ... ШӘШұЩғЩҠШ§ШЈЩ„Щ…Ш§ЩҶЩҠШ§ШіЩҲШұЩҠШ§Ш§Щ„Ш№ШұШ§ЩӮШЁЩ„ШәШ§ШұЩҠШ§Ш§Щ„ЩҲЩ„Ш§ЩҠШ§ШӘ Ш§Щ„Щ…ШӘШӯШҜШ©ЩҒШұЩҶШіШ§Ш§Щ„Щ…Щ…Щ„ЩғШ© Ш§Щ„Щ…ШӘШӯШҜШ©ЩҮЩҲЩ„ЩҶШҜШ§Ш§Щ„ЩҶЩ…ШіШ§ШЈШіШӘШұШ§Щ„ЩҠпҝҪ...

Software for concept mapping Example concept map created using the IHMC CmapTools computer program CmapTools is concept mapping software developed by the Florida Institute for Human and Machine Cognition (IHMC).[1] It allows users to easily create graphical nodes representing concepts, and to connect nodes using lines and linking words to form a network of interrelated propositions that represent knowledge of a topic.[2] The software has been used in classrooms and research la...

Former organized incorporated territory of the United States (1854вҖ“1867) Territory of NebraskaOrganized incorporated territory of the United States1854вҖ“1867CapitalOmaha вҖў TypeOrganized incorporated territory History вҖў KansasвҖ“Nebraska Act May 30, 1854вҖў Colorado Territory formed February 28, 1861вҖў Dakota Territory formed March 2, 1861вҖў Idaho Territory formed March 3, 1863вҖў Statehood March 1, 1867 Preceded by Succeeded by Unorganized terr...

French philosopher and sociologist Georges SorelGeorges SorelBornGeorges EugГЁne Sorel(1847-11-02)2 November 1847Cherbourg, FranceDied29 August 1922(1922-08-29) (aged 74)Boulogne-sur-Seine, FranceAlma materГүcole PolytechniqueNotable workReflections on Violence (1908)EraModern philosophy Fin de siГЁcle 20th-century philosophy RegionWestern philosophy French philosophy School Continental philosophy Sorelianism Revisionist Marxism National Syndicalism Irrationalism Main interests Scie...

Part of the LGBT rights seriesLegal status ofsame-sex unions Marriage Andorra Argentina Australia Austria Belgium Brazil Canada Chile Colombia Costa Rica Cuba Denmark Ecuador Estonia Finland France Germany Greece Iceland Ireland Liechtenstein* Luxembourg Malta Mexico Nepal Netherlands1 New Zealand2 Norway Portugal Slovenia South Africa Spain Sweden Switzerland Taiwan United Kingdom3 United States4 Uruguay Recognized Israel5 Civil unions andregistered partnerships Bolivia Croatia Cyprus Czech...

ЩҠЩҒШӘЩӮШұ Щ…ШӯШӘЩҲЩү ЩҮШ°ЩҮ Ш§Щ„Щ…ЩӮШ§Щ„Ш© ШҘЩ„Щү Ш§Щ„Ш§ШіШӘШҙЩҮШ§ШҜ ШЁЩ…ШөШ§ШҜШұ. ЩҒШ¶Щ„Ш§ЩӢШҢ ШіШ§ЩҮЩ… ЩҒЩҠ ШӘШ·ЩҲЩҠШұ ЩҮШ°ЩҮ Ш§Щ„Щ…ЩӮШ§Щ„Ш© Щ…ЩҶ Ш®Щ„Ш§Щ„ ШҘШ¶Ш§ЩҒШ© Щ…ШөШ§ШҜШұ Щ…ЩҲШ«ЩҲЩӮ ШЁЩҮШ§. ШЈЩҠ Щ…Ш№Щ„ЩҲЩ…Ш§ШӘ ШәЩҠШұ Щ…ЩҲШ«ЩӮШ© ЩҠЩ…ЩғЩҶ Ш§Щ„ШӘШҙЩғЩҠЩғ ШЁЩҮШ§ ЩҲШҘШІШ§Щ„ШӘЩҮШ§. (ШҜЩҠШіЩ…ШЁШұ 2018) ЩҮШ°ЩҮ ЩҮЩҠ ЩӮШ§ШҰЩ…Ш© Ш§Щ„ЩҶШ¬ЩҲЩ… ЩҒЩҠ ЩғЩҲЩғШЁШ© Щ…ЩҒШұШәШ© Ш§Щ„ЩҮЩҲШ§ШЎ (ШЁШ§Щ„ШҘЩҶШ¬Щ„ЩҠШІЩҠШ©: List of stars in Antlia)вҖҸ Ш§Щ„Ш§ШіЩ… ШӘШіЩ…ЩҠШ© ШЁШ§ЩҠШұ Ш§Щ„Щ…ШӘШәЩҠШұШ© ЩғШӘШ§Щ„ЩҲШ¬ пҝҪ...

Layers of grey and white matter that cover the upper surface of the cerebrum in vertebrates PalliumSchematic cross-section of the forebrain of a basal chordate such as a shark.Schematic illustration of differences in neuronal specification and migration patterns between the mammalian and avian palliumDetailsPart ofTelencephalonIdentifiersLatinpallium, or cortex cerebriNeuroLex IDbirnlex_1494TA98A14.1.09.003TA25527TE(neuroanatomy)_by_E5.14.3.4.3.1.30 E5.14.3.4.3.1.30 Anatomical terms of neuroa...

Parliamentary position of the Parliament of New Zealand Leader of the Official Opposition of New ZealandCoat of ArmsIncumbentChris Hipkinssince 27 November 2023Official Opposition of New ZealandReports toParliamentTerm lengthWhile leader of the largest political party in the House of Representatives that is not in governmentInaugural holderJohn Ballance[a]Formation2 July 1889[b]Salary$288,900 (As at 2016)[update][1]^ a. As the first parliamentary leader of an Opposition p...

Questa voce sull'argomento Calciatori tedeschi ГЁ solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Ben ZolinskiNazionalitГ Germania Altezza181 cm Peso78 kg Calcio RuoloCentrocampista Squadra Kaiserslautern CarrieraGiovanili -2006 Neubrandenburg2006-2011 Hansa Rostock Squadre di club1 2011 Hansa Rostock II0 (0)2011-2012вҶ’ Carl Zeiss Jena II12 (0)2012-2013 Hansa Rostock ...