三维投影
|
Read other articles:

Diagram Usenet beberapa server dan klien. Titik-titik biru, hijau, dan merah pada server yang merupakan kelompok-kelompok mereka bawa. Panah antara server menunjukkan bahwa server berbagi artikel dari kelompok. Panah antara komputer dan server menunjukkan bahwa pengguna berlangganan ke kelompok tertentu, dan upload dan artikel download ke dan dari server. Usenet adalah sistem diskusi Internet yang terdistribusi secara global. Sistem ini dikembangkan dari arsitektur serbaguna UUCP dari nama ya...

Patriark Melkit Gregorius III (tengah gambar) dengan beberapa Arkimandrit, mengunjungi Biara Bunda dari Caravaggio, Italia, pada 11 September 2008 Gelar arkimandrit (Yunani: ἀρχιμανδρίτης archimandritis), biasanya dipakai dalam gereja-gereja Ortodoks Timur dan Katolik Timur, awalnya merujuk kepada seorang kepala biara tertinggi yang dilantik oleh uskup untuk menaungi beberapa kepala biara 'biasa' (masing-masing disebut hegumenos) dan monasteri-monasteri, atau kepada kepala biara...

GeelongVictoriaGeelong CBD and Corio Bay from Moorpanyal Park North Shore in 2010.GeelongKoordinat38°09′S 144°21′E / 38.150°S 144.350°E / -38.150; 144.350Koordinat: 38°09′S 144°21′E / 38.150°S 144.350°E / -38.150; 144.350Jumlah penduduk160,991 (2006 Census)[1] (12th) • Kepadatan165,3/km2 (4.280/sq mi)Didirikan1836Kode pos3220Luas1.240 km2 (478,8 sq mi)Zona waktuAEST (UTC+10) • M...

This article is about the food. For other uses, see Sausage (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Sausage – news · newspapers · books · scholar · JSTOR (October 2022) (Learn how and when to remove this template message) Meat product Kiełbasa biała (white sausage), szynkowa (smok...

مقاطعة روتلاند خريطة الموقع تاريخ التأسيس 1781 تقسيم إداري البلد الولايات المتحدة [1][2] العاصمة روتلاند التقسيم الأعلى فيرمونت خصائص جغرافية إحداثيات 43°34′48″N 73°02′12″W / 43.58009°N 73.03661°W / 43.58009; -73.03661 [3] المساحة 2,447 كم² نسبة المياه ...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) 2007 في الهندمعلومات عامةالسنة 2007 2006 في الهند 2008 في الهند تعديل - تعديل مصدري - تعديل ويكي بيانات سنوات 2005: 200...

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...

Koordinat: 33°44′32″N 118°16′38″W / 33.7423°N 118.2772°W / 33.7423; -118.2772 Untuk kapal lain dengan nama serupa, lihat USS Iowa. Iowa menembakkan meriamnya. Sejarah Amerika Serikat Asal nama Negara bagian IowaDipesan 1 Juli 1939Pembangun New York Naval YardPasang lunas 27 Juni 1940Diluncurkan 27 Agustus 1942Sponsor Ilo WallaceMulai berlayar 22 Februari 1943Dipensiunkan 24 Maret 1949 Berlayar kembali 25 Agustus 1951Dipensiunkan 24 Februari 1958 Berlayar ke...

Pour les articles homonymes, voir Downey (homonymie). Robert Downey Jr. Robert Downey Jr. au Comic-Con de San Diegoen 2014. Données clés Nom de naissance Robert John Downey Junior Naissance 4 avril 1965 (59 ans)New York, État de New York, États-Unis Nationalité Américaine Profession ActeurScénariste Films notables ChaplinKiss Kiss Bang BangUnivers cinématographique MarvelTonnerre sous les tropiquesSherlock HolmesOppenheimer modifier Robert Downey Jr. /ˈɹɑbɚt ˈdaʊni ˈd͡ʒ...

提示:此条目页的主题不是中華人民共和國最高領導人。 中华人民共和国 中华人民共和国政府与政治系列条目 执政党 中国共产党 党章、党旗党徽 主要负责人、领导核心 领导集体、民主集中制 意识形态、组织 以习近平同志为核心的党中央 两个维护、两个确立 全国代表大会 (二十大) 中央委员会 (二十届) 总书记:习近平 中央政治局 常务委员会 中央书记处 �...

The Global Campaign for Equal Nationality RightsFormation2014TypeNGOPurposeGender Equality; Nationality Rights; activismHeadquartersNew YorkCampaign ManagerCatherine HarringtonWebsiteequalnationalityrights.org The Global Campaign for Equal Nationality Rights is a campaign mobilizes international action to end gender discrimination in nationality laws through local and international advocacy, activism, research, capacity building and knowledge sharing.[1] The Global Campaign for Equal ...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (مارس 2019) الانتخابات البرلمانية الأندلسية 2012 2012 البلد إسبانيا التاريخ 25 مارس 2012 الانتخابات البرلمانية الأندلسية 2008 [لغات أخرى] منصب عضو برلمان أند�...

Ruler of the Achaemenid Empire from 530 to 522 BC Cambyses II𐎣𐎲𐎢𐎪𐎡𐎹King of KingsGreat KingKing of PersiaKing of BabylonPharaoh of EgyptKing of CountriesCambyses (left, kneeling) as pharaoh while worshipping an Apis bull (524 BC)King of Kings of the Achaemenid EmpireReign530 – July 522 BCPredecessorCyrus the GreatSuccessorBardiyaCo-rulerCyrus the Great (530 BC)Pharaoh of EgyptReign525 – July 522 BCPredecessorPsamtik IIISuccessorBardiya Royal titulary Horus name ...

PBS and NPR member networks in Oregon OPB redirects here. For other uses, see OPB (disambiguation). KOTD redirects here. For the upcoming role-playing video game, see Kingdoms of the Dump. For the rap battle league, see King of the Dot. This article may rely excessively on sources too closely associated with the subject, potentially preventing the article from being verifiable and neutral. Please help improve it by replacing them with more appropriate citations to reliable, independent, third...
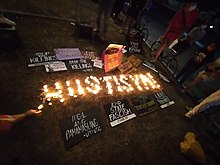
Human rights in the Philippines are protected by the Constitution of the Philippines, to make sure that people in the Philippines are able to live peacefully and with dignity, safe from the abuse of any individuals or institutions, including the state.[1][2] The concept and practice of human rights within the Philippines is defined by Article III of the Philippine Constitution,[3] as well as the United Nations' International Bill of Human Rights, to which the Philippi...

1950 film by William A. Berke The Bandit QueenThe Bandit Queen with her avenging bullwhipDirected byWilliam BerkeWritten byOrville H. Hampton(additional dialogue)Screenplay byVictor WestBudd LesserStory byVictor WestProduced byWilliam BerkeexecutiveRobert L. LippertMurray LernerStarringBarbara BrittonWillard ParkerPhillip ReedCinematographyErnest Miller(as Ernest W. Miller)Edited byCarl PiersonMusic byAlbert GlasserProductioncompanyLippert PicturesDistributed byLippert PicturesRelease dates D...

Overview of the events of 2011 in arthropod paleontology List of years in arthropod paleontology … 2008 2009 2010 2011 2012 2013 2014 … In paleontology 2008 2009 2010 2011 2012 2013 2014 In science 2008 2009 2010 2011 2012 2013 2014 In reptile paleontology 2008 2009 2010 2011 2012 2013 2014 In paleobotany 2008 2009 2010 2011 2012 2013 2014 In paleoentomology 2008 2009 2010 2011 2012 2013 2014 In paleomalacology 2008 2009 2010 2011 2012 2013 2014 In archosaur paleontology 2008 2009 2010 2...

Korea Open 2023DoppioSport Tennis Vincitori Marie Bouzková Bethanie Mattek-Sands Finalisti Luksika Kumkhum Peangtarn Plipuech Punteggio6-2, 6-1 Tornei Singolare Singolare (q) Doppio Doppio Voce principale: Korea Open 2023. Il doppio femminile del torneo di tennis professionistico Korea Open 2023, facente parte della categoria WTA 250 nell'ambito del WTA Tour 2023, si è giocato dal 9 al 15 ottobre 2023 a Seul, nella Corea del Sud. Kristina Mladenovic e Yanina Wickmayer erano le campio...



























