Đa giác lồi
|
Read other articles:

Napoleon Berkas:KucingNapoleon.jpg Nama lain Minuet Asal Amerika Serikat[1] Standar ras TICA standar Kucing domestik (Felis catus) Kucing napoleon (atau minuet) adalah salah satu ras kucing baru berbadan sedang yang merupakan hasil persilangan ras munchkin dengan persia. Keunikan dari ras kucing ini adalah memiliki kaki yang pendek.[2] Kucing ini berasal dari Amerika Serikat[1] dan pertama kali dikembangkan pada tahun 1995.[2] Sejarah Napoleon diciptakan...

Konstantinos Mitroglou Informasi pribadiTanggal lahir 12 Maret 1988 (umur 36)Tempat lahir Kavala, YunaniTinggi 1,88 m (6 ft 2 in)Posisi bermain StrikerInformasi klubKlub saat ini Atromitos F.C.Nomor 23Karier junior2004–2005 MSV Duisburg II2005–2007 Borussia Mönchengladbach IIKarier senior*Tahun Tim Tampil (Gol)2004-2005 MSV Duisburg II 12 (5)2005–2007 Borussia Mönchengladbach II 35 (38)2007– Olympiacos 48 (16)2010–2011 → Panionios (pinjaman) 11 (8)2011– �...

Deputi Bidang Koordinasi Pengelolaan Energi, Sumber Daya Alam, dan Lingkungan Hidup Kementerian Koordinator Bidang Perekonomian Republik IndonesiaGambaran umumDasar hukumPeraturan Presiden Nomor 8 Tahun 2015Susunan organisasiDeputiMontty Girianna[1]Kantor pusatGedung Ali Wardhana Jl. Lapangan Banteng Timur No.2-4, Jakarta Pusat 10710[2]Situs webwww.ekon.go.id Deputi Bidang Koordinasi Pengelolaan Energi, Sumber Daya Alam, dan Lingkungan Hidup merupakan unsur pelaksana pada...

Untuk suku semi-nomaden laut yang ada di Indonesia, lihat Suku Laut (Indonesia). Bangsa Laut bertempur melawan pasukan Mesir. Bangsa Laut (n3 ḫ3s.wt n<.t> p3 ym) Hieroglif Mesir Bangsa Laut atau Orang Laut adalah kumpulan pelaut yang menyerbu dan menjarah pada milenium kedua SM. Mereka belayar ke Laut Tengah timur, menyebabkan kerusuhan politik, dan berupaya memasuki atau menguasai wilayah Mesir pada akhir dinasti ke-19 dan khususnya selama tahun kedelapan pemerintahan Ramses III pada...
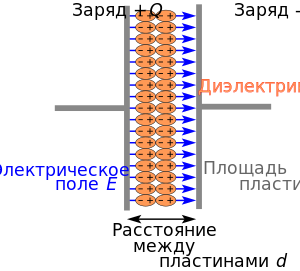
Иное название этого понятия — «изолятор»; см. также другие значения. Схема конденсатора с параллельными пластинами с диэлектриком. Две пластины с площадью A {\displaystyle A} находятся на расстоянии d {\displaystyle d} . Когда заряд ± Q {\displaystyle \pm Q} находится на пластинах, в промежут�...

Eno SigitLahirRetnosari Widowati Harjojudanto10 April 1974 (umur 49)IndonesiaPekerjaanpengusaha, penyanyiSuami/istriFahmi DavidAnakJibrilian AmelKarier musik Retnosari Widowati Harjojudanto yang lebih dikenal sebagai Eno Sigit (lahir 10 April 1974) adalah pengusaha Indonesia. Dulu putri kedua dari tiga bersaudara pasangan Sigit Hardjojudanto dan Ilsye Aneke Ratnawati ini sempat dikenal sebagai penyanyi dan sempat merilis album duet bersama Harry de Fretes. Album yang dirilis tahun 1996 ...

Town in Vermont, United StatesLemington, VermontTownLocation in Essex County and the state of Vermont.Location of Vermont in the United StatesCoordinates: 44°55′26″N 71°33′25″W / 44.92389°N 71.55694°W / 44.92389; -71.55694CountryUnited StatesStateVermontCountyEssexChartered1762Settled1789Organized1796Area • Total35.5 sq mi (92.0 km2) • Land35.4 sq mi (91.6 km2) • Water0.2 sq mi (0....

Inorganic compound (SOCl2) Thionyl chloride Names IUPAC name Thionyl chloride Other names Thionyl dichloride Sulfurous oxychloride Sulfinyl chloride Sulfinyl dichloride Dichlorosulfoxide Sulfur oxide dichloride Sulfur monoxide dichloride Sulfuryl(IV) chloride Identifiers CAS Number 7719-09-7 Y 3D model (JSmol) Interactive image ChEBI CHEBI:29290 Y ChemSpider 22797 Y ECHA InfoCard 100.028.863 EC Number 231-748-8 PubChem CID 24386 RTECS number XM5150000 UNII 4A8YJA13N4 N UN ...

Inbördeskriget i Nordjemen Rojalistiska jemenitiska styrkor försöker avvärja en egyptisk attack. Ägde rum 1962–1970 Plats Nordjemen Resultat Republikansk seger Saudiskt stöd till Iman al-Badr och rojalistiska fraktionen upphörde 1965. Tillbakadragande av egyptiska styrkor 1967. Stridande Kungariket Jemen SaudiarabienUnderstödda av: Jordanien Storbritannien* Europeiska legosoldater Arabrepubliken Jemen Förenade arabrepubliken Befälhavare och ledare I...

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...

Place in Queensland, AustraliaChinatown唐人街 (Chinese)Fortitude Valley, QueenslandEntrance, 2023LGA(s)City of Brisbane (Central Ward)State electorate(s)McConnellFederal division(s)Brisbane Brisbane ChinatownChinese布里斯班唐人街TranscriptionsStandard MandarinHanyu PinyinBù lǐsī bān tángrénjiē Chinatown, Brisbane (Chinese: 布里斯本唐人街) is a precinct in Fortitude Valley, Brisbane, Australia. It is centred on Chinatown Mall, a pedestrian street which oc...

Engagement of the Boshin War This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (April 2008) (Learn how and when to remove this message) Battle of Kōshū-KatsunumaPart of Boshin WarKondō Isami at the Battle of Kōshū-Katsunuma.Date29 March 1868LocationKatsunuma, YamanashiResult Imperial victoryBelligerents Satsuma, Chōshū, ...

Навчально-науковий інститут інноваційних освітніх технологій Західноукраїнського національного університету Герб навчально-наукового інституту інноваційних освітніх технологій ЗУНУ Скорочена назва ННІІОТ ЗУНУ Основні дані Засновано 2013 Заклад Західноукраїнський �...

Peter SarnakBiographieNaissance 18 décembre 1953 (70 ans)JohannesbourgNationalité américaineFormation Université StanfordUniversité du WitwatersrandActivités Mathématicien, professeur d'universitéAutres informationsA travaillé pour Institute for Advanced Study (depuis 2007)Université de Princeton (depuis 1991)Université Stanford (1984-1991)Université de New York (1980-2005)Membre de Royal Society (2002)Academia Europaea (2013)American Mathematical Society (2017)Académie amé...

2008 soundtrack album by John ZornFilmworks XX: Sholem AleichemSoundtrack album by John ZornReleasedSeptember 16, 2008Recorded2008Genreavant-garde, jazz, classicalLength44:32LabelTzadik TZ 7369ProducerJohn ZornJohn Zorn chronology The Art of Memory II(2008) Filmworks XX: Sholem Aleichem(2008) Filmworks XXI: Belle de Nature/The New Rijksmuseum(2008) Filmworks chronology Filmworks XIX: The Rain Horse(2008) Filmworks XX: Sholem Aleichem(2008) Filmworks XXI: Belle de Nature/The New Rijksm...

English clergyman and scholar (1849–1909) Old Court of Selwyn College, Cambridge, with the Hall on the right Richard Appleton MA (17 February 1849 – 1 March 1909) was an English scholar, clergyman of the Church of England, and the fourth Master of Selwyn College, Cambridge, 1907 – 1909. He was a fellow of Trinity College, Cambridge, and a parish priest before moving to Selwyn.[1] Early life Appleton was born in Liverpool, the son of another Revd Richard Appleton and grandson...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (نوفمبر 2019) كأس الرابطة الفرنسية 2018–19 تفاصيل الموسم كأس الرابطة الفرنسية النسخة 25 ...

IndiHomeLogo IndiHome by Telkomsel sejak 1 Juli 2023Nama sebelumnyaTelkomNet Instan (1994-2004)Speedy (2004-2015)JenisInternetTelepon rumah protokol internetTelevisi protokol internet berlanggananMotoSemua Rumah Semua Bisa (2020-2021)Aktivitas Tanpa Batas (2021-sekarang)SloganSemua Bisa Berubah Maju (2020-2021)Internetnya Indonesia (2021-sekarang)Negara IndonesiaTanggal peluncuran1994 (sebagai TelkomNet Instan)2015 (sebagai IndiHome)PemilikTelkomselInduk perusahaanTelkom IndonesiaS...

American rapper (born 1981) Safaree SamuelsSamuels in 2019BornSafaree Lloyd Samuels (1981-07-04) July 4, 1981 (age 43)New York City, U.S.Nationality American (jus soli) Jamaican (jus sanguinis)[1] Other namesSafareeScaffScaff BeezyVVS BeezyStuntmanEducationMidwood High SchoolOccupationsRappersongwritertelevision produceractorYears active2000–presentLabels916%StuntgangH2OX-RaySpouse Erica Mena (m. 2019; div. 2022)Chil...

International federation of sports for athletes with a vision impairment International Blind Sports FederationFormation1981; 43 years ago (1981)TypeSports federationHeadquartersBonn, Germany[1]PresidentIlgar RahimovWebsitewww.ibsasport.org The International Blind Sports Federation (IBSA) is a non-profit organisation founded 1981 in Paris, France. It was formerly known as the International Blind Sports Association. IBSA's mission is to promote the full integration of ...



