Số Bell
|
Read other articles:

Interdependence of human economies and natural ecosystems For the academic journal, see Ecological Economics (journal). Not to be confused with Environmental economics. Part of a series onEcological economicsHumanity's economic system viewed as a subsystem of the global environment Concepts Carbon fee and dividend Carrying capacity Ecological market failure Ecological model of competition Ecosystem services Embodied energy Energy accounting Entropy pessimism Index of Sustainable Economic Welf...

Aim and IgniteAlbum studio karya Fun (band)Dirilis25 Agustus 2009Direkam2008GenreIndie pop, alternative rock, baroque pop, neo-psychedeliaDurasi42:15LabelNettwerkProduserSteven McDonaldKronologi Fun (band) Aim and Ignite(2009) Some Nights(2012)Some Nights2012 Aim and Ignite adalah debut album studio dari band indie pop bernama Fun (band). Album ini dirilis pada tanggal 25 Agustus 2009 melalui Nettwerk. Judul album ini diambil dari lirik lagu Light a Roman Candle with Me Daftar lagu Be Cal...

Untuk pengertian lain, lihat Windsor. WindsorKotaCity of WindsorFoto dari atas ke bawah, kanan ke kiri: Downtown Windsor skyline, Ambassador Bridge, Charlie Brooks Memorial Peace Fountain, Dillon Hall di Universitas Windsor, dan Caesars Windsor.Julukan: The City of Roses, Automotive Capital of Canada[1] [2]Motto: The river and the land sustain us.Location of Windsor next to Essex County, in the province of OntarioNegaraKanadaProvinsiOntarioPembagian sensusEssexDihuni...

Perjalanan Tak TergantikanAlbum studio karya The RainDirilis10 Januari 2009Direkam2008GenrePop, rock, countryLabelNagaswaraKronologi The Rain Serenade(2007)Serenade2007 Perjalanan Tak Tergantikan(2009) Jingga Senja dan Deru Hujan(2012)Jingga Senja dan Deru Hujan2012 Perjalanan Tak Tergantikan adalah album keempat dari grup band The Rain yang dirilis pada tanggal 10 Januari 2009 melalui Nagaswara. Album ini melahirkan 4 single yaitu Boleh Saja Benci, Meninggalkan Cerita Ini, Percaya dan Pe...

Thai badminton player Badminton playerPornpawee ChochuwongChochuwong at the 2017 SEA Games.Personal informationCountryThailandBorn (1998-01-22) 22 January 1998 (age 26)Rayong, ThailandHeight1.70 m (5 ft 7 in)HandednessRightWomen's singlesHighest ranking8 (4 October 2022)Current ranking16 (30 January 2024) Medal record Women's badminton Representing Thailand Sudirman Cup 2017 Gold Coast Mixed team 2019 Nanning Mixed team Uber Cup 2018 Bangkok Women's team 20...

Pour les articles homonymes, voir Panic Button. Panic Button Données clés Titre original Panic Button Réalisation Chris Crow Scénario Chris CrowFrazer Lee Acteurs principaux Scarlett Alice Johnson Jack Gordon Michael Jibson Pays de production Royaume-Uni Genre Horreur Thriller Durée 96 minutes Sortie 2011 Pour plus de détails, voir Fiche technique et Distribution. modifier Panic Button est un film britannique réalisé par Chris Crow sorti en 2011 Synopsis Quatre gagnants d'un jeu en l...

Sceaux 行政国 フランス地域圏 (Région) イル=ド=フランス地域圏県 (département) オー=ド=セーヌ県郡 (arrondissement) アントニー郡小郡 (canton) 小郡庁所在地INSEEコード 92071郵便番号 92330市長(任期) フィリップ・ローラン(2008年-2014年)自治体間連合 (fr) メトロポール・デュ・グラン・パリ人口動態人口 19,679人(2007年)人口密度 5466人/km2住民の呼称 Scéens地理座標 北緯48度4...

Rovasenda komune di Italia Tempat Negara berdaulatItaliaRegion di ItaliaPiedmontProvinsi di ItaliaProvinsi Vercelli NegaraItalia Ibu kotaRovasenda PendudukTotal907 (2023 )GeografiLuas wilayah29,27 km² [convert: unit tak dikenal]Ketinggian221 m Berbatasan denganArborio Brusnengo Buronzo Gattinara Ghislarengo Masserano Roasio San Giacomo Vercellese Lenta SejarahSanto pelindungMaria Diangkat ke Surga Informasi tambahanKode pos13040 Zona waktuUTC+1 UTC+2 Kode telepon0161 ID ISTAT00212...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

Greek-British Marxist historian, long associated with Hull University For the actor, playwright and theatre manager, see John Faucit Saville. For those of a similar name, see John Savile (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: John Saville – news · newspapers · books · scholar · JST...

Henry Holiday, l'incontro immaginario fra Dante e Beatrice (con il vestito bianco) accompagnata dall'amica Vanna (con il vestito rosso), sul Ponte Santa Trinita in Firenze (1883) Beatrice Portinari, detta Bice, coniugata de' Bardi (Firenze, 1265/66 – Firenze, 8 giugno 1290), è, secondo alcuni critici letterari, la donna che Dante trasfigura nel personaggio di Beatrice, musa e ispiratrice del poeta. La sua morte causò a Dante una profonda crisi. Stemma Portinari Indice 1 Personaggio storic...
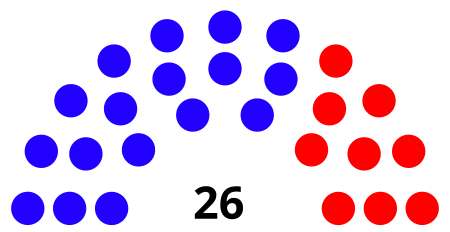
This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Louisville Metro Council – news · newspapers · books · scholar · JSTOR (January 2024) (Learn how and when to remove this message) Louisville Metro CouncilTypeTypeUnicameral of Louisville/Jefferson County Metro, KentuckyTerm limitsNoneHistoryFoundedJanuary ...

Syahril SabirinSyahril pada 1998 Gubernur Bank Indonesia ke-11Masa jabatanFebruari 1998 – Mei 2003PresidenSoehartoB. J. HabibieAbdurrahman WahidMegawati SoekarnoputriPendahuluSudrajad DjiwandonoPenggantiBurhanuddin Abdullah Informasi pribadiLahir14 Oktober 1943 (umur 80)Bukittinggi, Sumatera Barat, Masa Pendudukan JepangKebangsaanIndonesiaSuami/istriMurni Syahril SabirinAnakMelissa Sari SabirinStevano SabirinAlma materUniversitas Gajah MadaKolese WilliamsUniversitas Vander...

Francobollo che ritrae Felice Matteucci e Eugenio Barsanti Felice Matteucci (Lucca, 12 febbraio 1808 – Capannori, 13 settembre 1887) è stato un ingegnere e inventore italiano. Brevetto inglese per il motore Barsanti-Matteucci (12 giugno 1857) conservato presso l'archivio del Museo Galileo Modello del motore Barsanti-Matteucci all'osservatorio Ximeniano di Firenze Con Eugenio Barsanti realizzò il primo motore a combustione interna. Indice 1 Biografia 2 Opere 3 Dediche 4 Note 5 Bibliografia...

دوري الدرجة الأولى الروماني 1910–11 تفاصيل الموسم دوري الدرجة الأولى الروماني النسخة 2 البلد رومانيا التاريخ بداية:17 أكتوبر 1910 نهاية:6 فبراير 1911 المنظم اتحاد رومانيا لكرة القدم البطل أوليمبيا بوخارست مباريات ملعوبة 4 عدد المشاركين 3 دوري الدرجة...

French professional golfer (born 1990) Alexander Levy redirects here. For the Israeli architect, see Pagoda House. Alexander LévyPersonal informationNicknameEl Toro[1]Born (1990-08-01) 1 August 1990 (age 33)Orange, California, U.S.Height1.78 m (5 ft 10 in)Weight82 kg (181 lb; 12.9 st)Sporting nationality FranceResidenceBandol, FranceCareerTurned professional2011Current tour(s)European TourFormer tour(s)Challenge TourProfessional wins5Highest ra...

Hindu temple Anjaneya Temple, NanganallurReligionAffiliationHinduismDistrictChennaiDeityHanumanFestivalsHanumath Jayanthi, Gokulashtami, Sri Rama NavamiGoverning bodyHindu Religious & Charitable Endowments DepartmentLocationLocationNanganallurStateTamil NaduCountryIndiaLocation in Tamil NaduGeographic coordinates12°59′11″N 80°11′40″E / 12.986276°N 80.194308°E / 12.986276; 80.194308 This article needs additional citations for verification. Please help im...

NGC 843 Données d’observation(Époque J2000.0) Constellation Triangle Ascension droite (α) 02h 11m 08,2s[1] Déclinaison (δ) 35° 05′ 54″ Localisation dans la constellation : Triangle Astrométrie Caractéristiques physiques Liste des objets célestes modifier NGC 843 est constitué de trois étoiles située dans la constellation du Triangle. L'astronome prussien Heinrich d'Arrest[2] a enregistré la position de ces étoiles le 18 novembre 1865...

History of Kolkata, India The neutrality of this article is disputed. Relevant discussion may be found on the talk page. Please do not remove this message until conditions to do so are met. (September 2021) (Learn how and when to remove this message) Kolkata (formerly Calcutta) was a colonial city. The British East India Company developed Calcutta as a village by establishing an artificial riverine port in the 18th century CE. Kolkata was the capital of the British India until 1911, when the ...

Reservoir in PolandNyskie LakeNyskie LakeCoordinates50°27′27″N 17°16′51″E / 50.45750°N 17.28083°E / 50.45750; 17.28083TypereservoirPrimary inflowsNysa KłodzkaPrimary outflowsNysa KłodzkaBasin countriesPolandSurface area20 km2 (7.7 sq mi)Water volume124×10^6 m3 (101,000 acre⋅ft) Nyskie Lake (Polish: Jezioro Nyskie or Jezioro Głębinowskie) is a reservoir constructed on the Nysa Kłodzka river in Poland in 1971. Its name co...






![{\displaystyle B_{n}\sim {\frac {1}{\sqrt {n}}}\left[{\lambda \left(n\right)}\right]^{n+{\frac {1}{2}}}e^{\lambda \left(n\right)-n-1}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d208e268a6c641d268ac765f9462a4f17f02a824)
