Sóng trọng trường
|
Read other articles:

Don Goodman Informasi pribadiTanggal lahir 9 Mei 1966 (umur 57)Tempat lahir InggrisPosisi bermain PenyerangKarier senior*Tahun Tim Tampil (Gol)1998 Sanfrecce Hiroshima * Penampilan dan gol di klub senior hanya dihitung dari liga domestik Don Goodman (lahir 9 Mei 1966) adalah pemain sepak bola asal Inggris. Karier Don Goodman pernah bermain untuk Sanfrecce Hiroshima. Pranala luar (Jepang) Profil dan statistik di situs web resmi J. League Data Site Artikel bertopik pemain sepak bola Inggr...

The following is a list of Playboy Playmates of 1984, the 30th anniversary year of the publication. Playboy magazine names their Playmate of the Month each month throughout the year. January Main article: Penny Baker Penny BakerPersonal detailsBorn (1965-10-05) October 5, 1965 (age 58)Buffalo, New York[1]Height5 ft 8 in (1.73 m)[1] Penny Baker (born October 5, 1965)[1] is an American model and actress. After being interviewed in Chicago, she was ch...

Chronologies Données clés 1812 1813 1814 1815 1816 1817 1818Décennies :1780 1790 1800 1810 1820 1830 1840Siècles :XVIIe XVIIIe XIXe XXe XXIeMillénaires :-Ier Ier IIe IIIe Chronologies géographiques Afrique Afrique du Sud, Algérie, Angola, Bénin, Botswana, Burkina Faso, Burundi, Cameroun, Cap-Vert, République centrafricaine, Comores, République du Congo, République démocratique du Congo, Côte d'Ivoire, Djibouti, Égyp...

العلاقات المصرية الأردنية الأردن مصر السفارات سفارة مصر في الأردن السفير : خالد ثروت [1] العنوان : 7 شارع محمد علي بدير، عبدون، عمّان سفارة الأردن في مصر السفير : أمجد العضايلة [2] العنوان : 6 شارع باسم الخطيب، الدقي، ال...

Pemandangan kota Alicante Alicante merupakan nama kota di Spanyol. Letaknya 180 km dari Valencia. Luasnya 201,27 km² dan populasi 322.431 jiwa (2006). Artikel bertopik geografi atau tempat Spanyol ini adalah sebuah rintisan. Anda dapat membantu Wikipedia dengan mengembangkannya.lbs

English scholar and Orientalist (1854–1933) Palestine Under the Moslems: A Description of Syria and the Holy Land from A.D. 650 to 1500 Guy Le Strange (24 July 1854 – 24 December 1933) was a British Orientalist noted especially for his work in the field of the historical geography of the pre-modern Middle Eastern and Eastern Islamic lands, and his editing of Persian geographical texts.[1] He was a scholar of the Persian, Arabic, and Spanish languages. Le Strange was one of the ori...

Bashi adalah selat di utara Selat Luzon Selat Bashi (Hanzi sederhana: 巴士海峡; Hanzi tradisional: 巴士海峽; Pinyin: Bāshì hǎixiá) adalah suatu perairan yang bisa dilayari antara Pulau Mavulis (Pulau Y'Ami) di Filipina dan Pulau Anggrek di Taiwan. Selat ini merupakan bagian dari Selat Luzon di Samudra Pasifik. Selat ini memiliki ciri khas berupa badai selama musim hujan, Juni sampai Desember. Selat Bashi merupakan jalur penting bagi operasi militer. Taiwan dan Filipina...

Malaysian convenience store chain This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: KK Super Mart – news · newspapers · books · scholar · JSTOR (November 2021) (Learn how and when to remove this message) KK Supermart & Superstore Sdn. Bhd.Trade nameKK Super MartCompany typePrivate limited companyIndustryGrocery stores, convenience stores, retailFounde...

Sri LankaNickname(s)Tuskers, Brave Elephants[1]EmblemElephantUnionSri Lanka RugbyHead coachAaron DunneCaptainSrinath SooriyabandaraMost capsSrinath Sooriyabandara {74} First colours Second colours World Rugby rankingCurrent 41 (as of 6 May 2024)Highest37 (29 June 2015)Lowest64 (26 April 2004)First international All Ceylon 6–33 New Zealand (12 September 1907)Biggest win Sri Lanka 75–3 Pakistan (27 October 2004)Biggest defeat Japan 129–6 Sri Lanka ...

County in Mississippi, United States County in MississippiForrest CountyCountyHattiesburg Municipal Court.Location within the U.S. state of MississippiMississippi's location within the U.S.Coordinates: 31°11′N 89°16′W / 31.19°N 89.26°W / 31.19; -89.26Country United StatesState MississippiFounded1908[1]Named forNathan B. ForrestSeatHattiesburgLargest cityHattiesburgArea • Total470 sq mi (1,200 km2) • Land4...

Karate event in Budapest 2023 World ChampionshipsVenueLászló Papp Budapest Sports ArenaLocation Budapest, HungaryDates24–29 October← Dubai 2021Cairo 2025 → The 2023 World Karate Championships was held from 24 to 29 October 2023 in Budapest, Hungary.[1][2][3] Iranian team's visa problems The visas of 21 Iranian karateka were not issued for various reasons.[4] These karatekas were present in the men's kata and the women's committee.[...

此條目可参照烏克蘭語維基百科、英語維基百科和波蘭語維基百科相應條目来扩充,其中部分條目在對應語言版為高品質條目。 (2023年10月24日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 此条目页的主題...

Protein-coding gene in the species Homo sapiens FANCD2IdentifiersAliasesFANCD2, FA-D2, FA4, FACD, FAD, FAD2, FANCD, Fanconi anemia complementation group D2, FA complementation group D2External IDsOMIM: 613984; MGI: 2448480; HomoloGene: 13212; GeneCards: FANCD2; OMA:FANCD2 - orthologsGene location (Human)Chr.Chromosome 3 (human)[1]Band3p25.3Start10,026,370 bp[1]End10,101,932 bp[1]RNA expression patternBgeeHumanMouse (ortholog)Top expressed intesticleventricular zoneseco...

Peggy SaundersNazionalità Regno Unito Tennis Carriera Singolare1 Vittorie/sconfitte Titoli vinti Miglior ranking Risultati nei tornei del Grande Slam Australian Open - Roland Garros - Wimbledon 4R (1929) US Open QF (1929) Doppio1 Vittorie/sconfitte Titoli vinti Miglior ranking Risultati nei tornei del Grande Slam Australian Open - Roland Garros F (1927) Wimbledon V (1928, 1929) US Open V (1929) Doppio misto1 Vittorie/sconfitte Titoli vinti...

روبرتو أيالا (بالإسبانية: Roberto Ayala) معلومات شخصية الميلاد 14 أبريل 1973 (العمر 51 سنة)بارانا، انتري ريوس الطول 1.77 م (5 قدم 9 1⁄2 بوصة) مركز اللعب مدافع الجنسية الأرجنتين معلومات النادي النادي الحالي الأرجنتين (field assistant)[1] مسيرة الشباب سنوات فريق فيرو كاريل ...
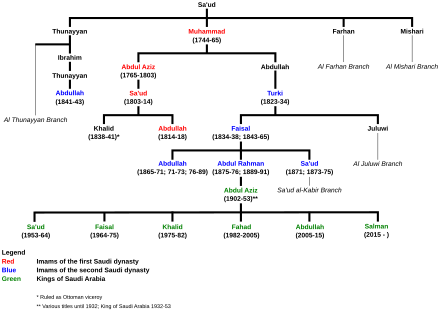
Genealogische Tabelle der Führer der Āl Saud Die Saudi-Dynastie (arabisch آل سعود Al Sa'ud, DMG Āl Saʿūd, dt.: ‚Nachkommen von Saʿūd‘) ist eine seit etwa 1735 existierende arabische Dynastie auf der Arabischen Halbinsel. Seit 1932 sind die Saud die Herrscherdynastie des Königreiches Saudi-Arabien. Die Königsfamilie ist weit verzweigt. Der Gründer des modernen Saudi-Arabien, König Abd al-Aziz ibn Saud, hatte schätzungsweise eintausend Enkel.[1] Nach Schä...

French writer, archaeologist and historian (1803–1870) For the French national heritage database, see Base Mérimée. Prosper MériméeBorn(1803-09-28)28 September 1803Paris, FranceDied23 September 1870(1870-09-23) (aged 66)Cannes, FranceOccupationWriter, historian, archaeologistSenator (1853–1870), member of the Académie Française (elected 1844)Literary movementRomanticismNotable worksLa Vénus d'Ille (1837)Carmen (1845)ParentsLéonor Mérimée (father)RelativesAugustin-Jean Fresn...

Reporter appointed by an organization to report on its meeting proceedings A rapporteur is a person who is appointed by an organization to report on the proceedings of its meetings. The term is a French-derived word. For example, Dick Marty was appointed rapporteur by the Parliamentary Assembly of the Council of Europe to investigate extraordinary rendition by the CIA. Rapporteur of the European Parliament The rapporteur is an eminent role in the legislative process of the European Parliament...

لمعانٍ أخرى، طالع غود هوب (توضيح). غود هوب الإحداثيات 34°06′32″N 86°52′02″W / 34.108777°N 86.867164°W / 34.108777; -86.867164 [1] تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة كولمان خصائص جغرافية المساحة 20.672727 كيلومتر مربع20.672689 كيلومتر م...

سفر أيوبمعلومات عامةاللغة العبرانية العنوان الأصلي אִיוֹב (بالعبرية) النوع الأدبي أداب الحكمه شخصيات القائمة ... أيوبElihu (en) Zophar (en) Eliphaz (en) Bildad (en) يهوهالشيطان التقديمالأجزاء القائمة ... سفر أيوب 10 سفر أيوب 11 سفر أيوب 12 سفر أيوب 14 سفر أيوب 15 سفر أيوب 16 سفر أيوب 17 سفر أيوب 18 ...