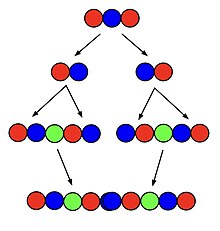
Siêu hoán vị

Các hoán vị trong siêu hoán vị có 3 dấu.

Trong toán học tổ hợp, siêu hoán vị trên n dấu là xâu mà mọi hoán vị của n dấu đó đều là xâu con của xâu đó. Mặc dù xâu siêu hoán vị tầm thường có thể tìm thấy ngay bằng cách nối tất cả các hoán vị lại với nhau, ta có thể tìm thấy các siêu hoán vị có độ dài nhỏ hơn (ngoại trừ trường hợp n = 1) vì các hoán vị được phép chèn lên nhau. Ví dụ chẳng hạn, trong trường hợp n = 2, siêu hoán vị 1221 chứa mọi hoán vị cần có (12 và 21), nhưng mà xâu ngắn hơn 121 cũng chứa đủ hai hoán vị đó.

Hiện đã được chứng minh rằng cho 1 ≤ n ≤ 5, siêu hoán vị cho n dấu có độ dài 1! + 2! + ... + n! (dãy số A180632 trong bảng OEIS). Bốn siêu hoán vị cho 1, 2, 3 và 4 dấu có độ dài tương ứng là 1, 3, 9, và 33, và các xâu tương ứng là 1, 121, 123121321, và 123412314231243121342132413214321. Tuy nhiên, đối với n = 5, có nhiều xâu hoán vị nhỏ nhất có độ dài 153. Một trong các số đó được biểu diễn ở dưới đây, một xâu khác có cùng độ dài có thể thu được từ xâu này bằng cách đổi tất cả các vị trí của tất cả của bốn và năm ở nửa sau của xâu (đằng sau số 2 in đậm):[1]

123451234152341253412354123145231425314235142315423124531243512431524312543121345213425134215342135421324513241532413524132541321453214352143251432154321

Đối với n > 5, siêu hoán vị nhỏ nhất chưa được tìm thấy và cũng chưa có cách để nhận dạng và tìm chúng, nhưng đã có các cận trên và cận dưới cho độ dài các xâu đó.

Tìm siêu hoán vị

Sơ đồ hình thành siêu hoán vị của 3 dấu từ siêu hoán vị có hai dấu.

Một trong những thuật toán hay dùng để tìm siêu hoán vị có dấu là thuật toán đệ quy. Đầu tiên, siêu hoán vị có cấp được tách thành các hoán vị theo thứ tự xuất hiện trong siêu hoán vị. Sau đó, mỗi hoán vị này sau đó được đặt ngay cạnh bản sao của chúng cùng với ký hiệu thứ n đứng giữa.Cuối cùng, các xâu thu được được xếp cạnh nhau và các dấu giống nhau và cạnh nhau thì sẽ hợp về còn một.[2]

Lấy ví dụ, siêu hoán vị cấp 3 có thể được tạo từ siêu hoán vị có 2 dấu; bắt đầu từ siêu hoán vị 121 và tách nó thành hai hoán vị 12 và 21, các hoán vị được sao lại và thêm vào thành 12312 và 21321. Sau đó đặt chúng cùng nhau thu được 1231221321, Các dấu 2 đứng giữa hợp lại với nhau thành siêu hoán vị 123121321 có 3 dấu. Thuật toán này cho phép tìm siêu hoán vị ngắn nhất cho mọi n nhỏ hơn hoặc bẳng 5, tuy nhiên kết quả sẽ càng trở nên dài hơn siêu hoán vị ngắn nhất khi n lớn dần.[2]

Cách khác để tìm siêu hoán vị là dựa trên xây đồ thị mà mỗi hoán vị là một đỉnh, và các hoán vị được nối với nhau bằng các cạnh có trọng số. Trọng số của mỗi cạnh được tính bằng cách đếm số dấu có thể thêm vào cuối hoán vị (và bỏ cùng số lượng đó ở đầu hoán vị) để thành hoán vị kia.[2] Lấy ví dụ, cạnh từ 123 đến 312 có trọng số 2 vì 123 + 12 = 12312 = 312. Bất kỳ đường đi Hamilton qua đồ thị này đều là siêu hoán vị, và bài toán tìm đường đi có trọng số ngắn nhất trở thành bài toán người đi du lịch. Siêu hoán vị đầu tiên có độ dài nhỏ hơn được tìm thấy trên máy tính theo phương pháp này là của Robin Houston.[3]

Cận dưới và cận trên

Thuật toán tìm siêu hoán vị nhỏ nhất cho xâu có nhiều hơn hoặc bằng 6 dấu hiện vẫn chưa được tìm thấy.[4] Tuy nhiên, có nhiều bài chứng minh gần đây đã thu hẹp lại cận trên và cận dưới của bài toán.[5]

Cận dưới, hay bài toán Haruhi

Vào tháng 9 năm 2011, một người dùng ẩn danh trên board Science & Math ("/sci/") của 4chan đã chứng minh được rằng siêu hoán vị nhỏ nhất trên n dấu (với n ≥ 2) có độ dài ít nhất n! + (n−1)! + (n−2)! + n − 3.[4] Lấy cảm hứng từ bộ anime Haruhi Suzumiya của Nhật Bản, bài toán trên diễn đàn được gọi là "bài toán Haruhi":[6] nếu bạn muốn xem hết 14 tập của mùa đầu tiên của bộ trong mọi thứ tự có thể, thì xâu ngắn nhất của các tập mà bạn cần xem là gì?[7] Bài chứng minh cho cận dưới này nhận được chú ý của cộng đồng vào tháng 10 năm 2018, sau khi nhà toán học và khoa học máy tính Robin Houston đã tweet về nó.[4] Vào ngày 25 tháng 10 năm 2018, Robin Houston, Jay Pantone, và Vince Vatter đã tải bản chứng minh đã được sửa lên bảng tra cứu dãy số nguyên trực tuyến (OEIS).[7][8] Phiên bản được xuất bản có ghi danh "người dùng nặc danh 4chan" và xuất hiện trong bài viết của Engen và Vatter (2019).[9] Riêng "bài toán Haruhi" (trường hợp có 14 dấu), cận dưới và cận trên hiện tại tương ứng là 93,884,313,611 và 93,924,230,411.[4] Điều này có nghĩa là để xem hết 14 tập đầu tiên trong mọi thứ tự có thể sẽ mất khoảng 4 triệu năm.

Cận trên

Vào ngày 20 tháng 10 năm 2018, sử dụng cách xây dựng của Aaron Williams cho các đường đi Hamilton qua đồ thị Cayley của nhóm đối xứng,[10] tác giả khoa học viễn tưởng và là nhà toán học Greg Egan đã đưa thuật toán có thể sinh ra siêu hoán vị có độ dài n! + (n−1)! + (n−2)! + (n−3)! + n − 3.[2] Tính đến hết năm 2018, đây là các siêu hoán vị duy nhất được biết đến và tìm thấy cho n ≥ 7. Tuy nhiên, vào ngày 2 tháng 1 năm 2019, Bogdan Coanda đã công bố tìm được siêu hoán vị cho n=7 có độ dài 5907, hay (n! + (n−1)! + (n−2)! + (n−3)! + n − 3) − 1, lập kỷ lục mới cho giá trị cận.[2] Vào 27 tháng 2 năm 2019, sử dụng các ý tưởng được phát triển bởi Robin Houston, Egan đã tìm ra siêu hoán vị cho n = 7 có độ dài 5906.[2] Câu hỏi rằng liệu có siêu hoán vị nào nhỏ hơn tồn tại cho n > 7 vẫn là câu hỏi mở. Cận dưới lớn nhất cho n = 7 vẫn là 5884.

Xem thêm

Đọc thêm

  • Ashlock, Daniel A.; Tillotson, Jenett (1993), “Construction of small superpermutations and minimal injective superstrings”, Congressus Numerantium, 93: 91–98, Zbl 0801.05004
  • Anonymous 4chan Poster; Houston, Robin; Pantone, Jay; Vatter, Vince (25 tháng 10 năm 2018). “A lower bound on the length of the shortest superpattern” (PDF). On-Line Encyclopedia of Integer Sequences.

Tham khảo

  1. ^ Johnston, Nathaniel (28 tháng 7 năm 2013). “Non-uniqueness of minimal superpermutations”. Discrete Mathematics. 313 (14): 1553–1557. arXiv:1303.4150. Bibcode:2013arXiv1303.4150J. doi:10.1016/j.disc.2013.03.024. S2CID 12018639. Zbl 1368.05004. Truy cập ngày 16 tháng 3 năm 2014.
  2. ^ a b c d e f Egan, Greg (20 tháng 10 năm 2018). “Superpermutations”. gregegan.net. Truy cập ngày 15 tháng 1 năm 2020.
  3. ^ Houston, Robin (21 August 2014). "Tackling the Minimal Superpermutation Problem". arΧiv:1408.5108 [math.CO]. 
  4. ^ a b c d Griggs, Mary Beth (24 tháng 10 năm 2018). “An anonymous 4chan post could help solve a 25-year-old math mystery”. The Verge.
  5. ^ Houston, Robin (21 tháng 8 năm 2014). “Tackling the Minimal Superpermutation Problem”. arXiv:1408.5108 [cs, math].
  6. ^ Anon, - San (17 tháng 9 năm 2011). “Permutations Thread III ニア愛”. Warosu.
  7. ^ a b Klarreich, Erica (5 tháng 11 năm 2018). “Sci-Fi Writer Greg Egan and Anonymous Math Whiz Advance Permutation Problem”. Quanta Magazine (bằng tiếng Anh). Truy cập ngày 21 tháng 6 năm 2020.
  8. ^ Anonymous 4chan poster; Houston, Robin; Pantone, Jay; Vatter, Vince (25 tháng 10 năm 2018). “A lower bound on the length of the shortest superpattern” (PDF). OEIS. Truy cập ngày 27 tháng 10 năm 2018.
  9. ^ Engen, Michael; Vatter, Vincent (2021), “Containing all permutations”, American Mathematical Monthly, 128 (1): 4–24, doi:10.1080/00029890.2021.1835384
  10. ^ Aaron, Williams (2013). "Hamiltonicity of the Cayley Digraph on the Symmetric Group Generated by σ = (1 2 ... n) and τ = (1 2)". arΧiv:1307.2549v3 [math.CO]. 

Liên kết ngoài

Read other articles:

Gwatʼsinux

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Gwatʼsinux – news · newspapers · books · scholar · JSTOR (May 2022) (Learn how and when to remove this template message) A Gwat'sinux man sits with a carved wooden bowl The Gwat'sinux or Quatsino, for whom Quatsino Sound on northern Vancouver Island is named, are one of the mai...

 

Eritroblastosis fetalis

Eritroblastosis fetalis adalah kelainan darah yang berpotensi mengancam nyawa janin atau bayi yang baru lahir.[1] Eritroblastosis fetalis umumnya disebabkan terjadinya isoimunisasi, yaitu proses pembentukan antibodi terhadap antigen individu lain yang berbeda.[2][3][4] Kelahiran anak pertama belum terkena dampak serius dari eritroblastosis fetalis, tetapi kelahiran anak berikutnya akan menimbulkan komplikasi.[2] Sebab Eritroblastosis fetalis biasanya te...

 

Sebastián Mora

Not to be confused with Sebastián Mora-Mora. Spanish racing cyclist Sebastián MoraMora during the 2017 Tour SeriesPersonal informationBornSebastián Mora Vedri (1988-02-19) 19 February 1988 (age 36)Villarreal, SpainHeight1.81 m (5 ft 11 in)Weight70 kg (154 lb)Team informationCurrent teamBurgos BHDisciplinesTrackRoadRoleRiderAmateur teams2007Würth2009–2010Asfaltos Guerola–CA Valencia Terra i Mar2011–2012UPV–Bancaja–CC Alginet2013Atika Sport–Asm...

Connollystraße

Street in Munich, Germany Connollystraße with a fountain The Connollystraße is a street in the Olympic Village and student quarter of the Olympic Park Munich. Description The street was named in 1971 after James Brendan Connolly, the first Olympic champion of the modern era (1896). It leads from the Helene-Mayer-Ring to the Kusocinskidamm to Straßbergerstraße. The road is accessible on the surface for pedestrians and cyclists, underground for motorists. Access is via the Lerchenauer Stra�...

 

Carl West Rich

American politician This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (August 2014) (Learn how and when to remove this template message) Carl West RichMember of the U.S. House of Representativesfrom Ohio's first districtIn officeJanuary 3, 1963 – January 3, 1965Preceded byGordon H. SchererSucceeded byJohn...

 

Kementerian Pertahanan Nasional (Meksiko)

Kementerian Pertahanan Nasional MeksikoSecretaría de la Defensa Nacional (SEDENA)LogoInformasi Kementerian PertahananDibentuk1821 (1821) (sebagai Kementerian Perang dan Angkatan Laut)Nomenklatur Kementerian Pertahanan sebelumnyaKementerian Perang dan Angkatan Laut (1821–1937)Wilayah hukum MeksikoKantor pusatBoulevard Manuel Ávila Camacho S/N. Esq. Av. Ind. Mil. Col. Lomas de Sotelo; Deleg. Miguel Hidalgo Mexico City, 1120019°26′25″N 99°12′57″W / 19.4402...

Myrtle Avenue, Hounslow

Street in the London Borough of Hounslow A Boeing 747-400 of Qantas approaching Heathrow Airport's runway 27L in 2004 over Myrtle Avenue A view of the airport from Myrtle Avenue, July 2020. Visible in the centre of the image is Concorde G-BOAB, which has been present at the airport since landing there in 2000. Myrtle Avenue is a street in the London Borough of Hounslow which is near the eastern end of Heathrow Airport's south runway, 27L.[1] This makes it noisy when aircraft are landi...

 

Taylor Walls

American baseball player (born 1996) Baseball player Taylor WallsWalls in 2017 with the Hudson Valley RenegadesTampa Bay Rays – No. 6Shortstop / Second basemanBorn: (1996-07-10) July 10, 1996 (age 27)Cordele, Georgia, U.S.Bats: SwitchThrows: RightMLB debutMay 22, 2021, for the Tampa Bay RaysMLB statistics (through 2023 season)Batting average.189Home runs17Runs batted in84 Teams Tampa Bay Rays (2021–present) Davis Taylor Walls (born July 10, 1996) is an American profess...

 

Joe Mercer

Joe Mercer Informasi pribadiNama lengkap Joseph MercerTanggal lahir 9 August 1914Tempat lahir Ellesmere Port, Cheshire, InggrisTanggal meninggal 9 Agustus 1990(1990-08-09) (umur 76)Tempat meninggal InggrisPosisi bermain gelandang kiriKarier junior Ellesmere PortKarier senior*Tahun Tim Tampil (Gol)1932–1946 Everton 170 (1)1946–1955 Arsenal 247 (2)Tim nasional1938–1939 Inggris 5 (0)Kepelatihan1955–1958 Sheffield United1958–1964 Aston Villa1965–1971 Manchester City1972–1974 C...

Человек прямоходящий

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...

 

Stasiun Palur

Stasiun Palur Y13 Bangunan baru Stasiun Palur, 2019LokasiDagen, Jaten, Karanganyar, Jawa Tengah 57764IndonesiaKoordinat7°34′1″S 110°52′29″E / 7.56694°S 110.87472°E / -7.56694; 110.87472Koordinat: 7°34′1″S 110°52′29″E / 7.56694°S 110.87472°E / -7.56694; 110.87472Ketinggian+93 mOperator KAI Commuter Letakkm 256+484 lintas Surabaya Kota-Kertosono-Madiun-Solo Balapan[1] Jumlah peron3 (satu peron sisi yang cukup tinggi...

 

Jacques Hadamard

Jacques HadamardJacques Salomon HadamardLahir(1865-12-08)8 Desember 1865Versailles, PrancisMeninggal17 Oktober 1963(1963-10-17) (umur 97)Paris, PrancisKebangsaanPrancisAlmamaterÉcole Normale SupérieureDikenal atasperkalian HadamardBukti dari teorema bilangan primamatriks HadamardPenghargaanGrand Prix des Sciences Mathématiques (1892)Prix Poncelet (1898) CNRS Gold medal (1956)Karier ilmiahBidangMatematikaInstitusiUniversitas BordeauxSorbonneCollège de FranceÉcole PolytechniqueÉcole...

Peppermint - L'angelo della vendetta

Peppermint - L'angelo della vendettaJennifer Garner in una scena del filmTitolo originalePeppermint Lingua originaleinglese Paese di produzioneStati Uniti d'America Anno2018 Durata102 minuti Genereazione, thriller RegiaPierre Morel SoggettoChad St. John SceneggiaturaChad St. John ProduttoreGary Lucchesi, Tom Rosenberg, Richard S. Wright Produttore esecutivoGary Lucchesi Casa di produzioneLakeshore Entertainment, Huayi Brothers, Tang Media Productions Distribuzione in italianoSTX Films, Lu...

 

Западный округ (Краснодар)

У этого термина существуют и другие значения, см. Западный округ. Западный внутригородской округ город Краснодар Дата основания 1936 год Дата упразднения 1994 Прежние имена Кагановичский, Ленинский районы Микрорайоны Дубинка, Черёмушки, Покровка Площадь 22[1]  км² Насе...

 

华盛顿州

  关于与「华盛顿州」標題相近或相同的条目页，請見「华盛顿」。   此條目介紹的是美國西北部太平洋沿岸的州。关于与之同名的美国首都所在地，请见「華盛頓哥伦比亚特区」。 此條目需要擴充。 (2007年9月26日)请協助改善这篇條目，更進一步的信息可能會在討論頁或扩充请求中找到。请在擴充條目後將此模板移除。 华盛顿州 美國联邦州State of Washington...

2016年美國總統選舉

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 %   获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

 

هواية جمع الطوابع

تعتبر هواية جمع طوابع البريد من أكثر الهوايات انتشارًا في العالم وهي هواية تثقيفية تؤدي إلى اهتمام أصحابها بالتطورات التاريخية للبلد الذي يجمعوا طوابعها.[1][2][3] البدايات الأولى بيني بلاك أول طابع بريد في العالم بدأت الهواية مع إصدار أول طابع بريد في بريطانيا ع�...

 

Arginina

Questa voce o sezione sull'argomento biochimica non è ancora formattata secondo gli standard. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Argininaformula di struttura Nome IUPACacido 2(S)-ammino-5-guanidilpentanoico AbbreviazioniRARG Nomi alternativiL-arginina acido α-ammino-δ-guanidinvalerianico Caratteristiche generaliFormula bruta o molecolareC6H14N4O2 Massa molecolare (u)174,20 Aspettosolido cristallino biancas...

中華民國國軍中的中共間諜列表

 本表是動態列表，或許永遠不會完結。歡迎您參考可靠來源來查漏補缺。 潛伏於中華民國國軍中的中共間諜列表收錄根據公開資料來源，曾潛伏於中華民國國軍、被中國共產黨聲稱或承認，或者遭中華民國政府調查審判，為中華人民共和國和中國人民解放軍進行間諜行為的人物。以下列表以現今可查知時間為準，正確的間諜活動或洩漏機密時間可能早於或晚於以下所歸�...

 

Francesco Rizzo (footballer)

Italian footballer (1943–2022) Francesco Rizzo Rizzo with Bologna in 1970Personal informationDate of birth (1943-05-30)30 May 1943Place of birth Rovito, ItalyDate of death 17 July 2022(2022-07-17) (aged 79)Height 1.73 m (5 ft 8 in)Position(s) MidfielderYouth career1959–1960 CosenzaSenior career*Years Team Apps (Gls)1960–1961 Cosenza 1961 AC Milan 1961–1962 Alessandria 1962–1968 Cagliari 1968–1970 Fiorentina 47 (8)1970–1972 Bologna 53 (4)1972–1974 Catanzaro ...