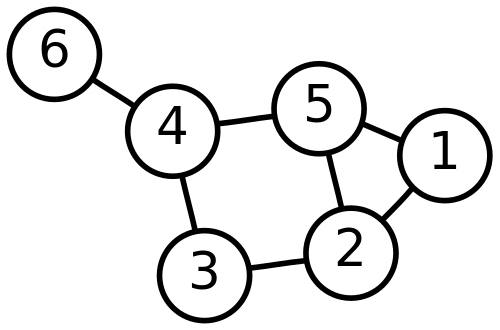
Ma trận Laplace

Trong lý thuyết đồ thị, ma trận Laplace, hay còn gọi là ma trận Kirchhoff, hoặc ma trận dẫn nạp, là một cách biểu diễn đồ thị bằng ma trận. Theo định lý Kirchhoff, nó có thể dùng để tính số cây bao trùm của đồ thị. Ma trận Laplace cũng cung cấp nhiều thông tin khác về đồ thị; có thể xem chi tiết hơn ở lý thuyết phổ đồ thị. Bất đẳng thức Cheeger trong hình học Riemann cũng có một dạng rời rạc sử dụng ma trận Laplace. Nó có thể dùng để tính xấp xỉ lát cắt thưa nhất (tiếng Anh - sparsest cut) của đồ thị thông qua giá trị đặc trưng thứ hai của ma trận Laplace.

Định nghĩa

Cho một đồ thị G = (V, E) với tập hợp đỉnh V và tập hợp cạnh E, cùng với một hàm trọng số $w:E\rightarrow \mathbb {R} ^{+}$ ( $\mathbb {R} ^{+}$ dùng để chỉ tập hợp số thực dương). Ma trận kề A_G của đồ thị được định nghĩa như sau:

A_{G}(i,j):={\begin{cases}w(i,j)&khi\ (i,j)\in E\\0&khi\ (i,j)\not \in E\end{cases}}

Ma trận bậc D_G là một ma trận đường chéo được định nghĩa như sau:

D_{G}(i,i):=\sum _{j}A_{G}(i,j)

Ma trận Laplace L_G được định nghĩa bởi^[1]^[2]

L_{G}=D_{G}-A_{G}

Có một định nghĩa khác tương đương như sau. Định nghĩa ma trận Laplace L_e của một cạnh e=(i,j) là ma trận với L_e(i,i)=L_e(j,j)=1 và L_e(i,j)=L_e(j,i)=-1. Ma trận L_G được định nghĩa bởi

L_{G}=\sum _{e\in E}w_{e}L_{e}

Ví dụ

Dưới đây là một ví dụ đơn giản về một đồ thị có nhãn, vô hướng và ma trận Laplace của nó.

Dán nhãn đồ thị	Ma trận bậc	Ma trận kề	Ma trận Laplace
	${\textstyle \left({\begin{array}{rrrrrr}2&0&0&0&0&0\\0&3&0&0&0&0\\0&0&2&0&0&0\\0&0&0&3&0&0\\0&0&0&0&3&0\\0&0&0&0&0&1\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrrrrr}0&1&0&0&1&0\\1&0&1&0&1&0\\0&1&0&1&0&0\\0&0&1&0&1&1\\1&1&0&1&0&0\\0&0&0&1&0&0\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrrrrr}2&-1&0&0&-1&0\\-1&3&-1&0&-1&0\\0&-1&2&-1&0&0\\0&0&-1&3&-1&-1\\-1&-1&0&-1&3&0\\0&0&0&-1&0&1\\\end{array}}\right)}$

Tính chất

Với bất kì đồ thị G nào cùng với ma trận Laplace tương ứng với các giá trị đặc trưng $\lambda _{0}\leq \lambda _{1}\leq \cdots \leq \lambda _{n-1}$ :

L luôn xác định không âm ( $\forall i,\lambda _{i}\geq 0;\quad \lambda _{0}=0$ ).
Số giá trị đặc trưng của ma trận Laplace nhận giá trị 0 là số thành phần liên thông của đồ thị.
$\lambda _{0}$ luôn bằng 0 do mọi ma trận Laplace đều có vectơ đặc trưng $[1,1,\dots ,1]$ tương ứng với giá trị đặc trưng 0.

Ghi chú

^ Weisstein, Eric W., "Laplacian Matrix" từ MathWorld.
^ “Bài giảng thứ 2 lớp của Dan Spielman” (PDF). Bản gốc (PDF) lưu trữ ngày 24 tháng 1 năm 2012. Truy cập ngày 11 tháng 9 năm 2011. Chú thích có tham số trống không rõ: |3= (trợ giúp)

Read other articles:

Stasiun Taiyō

Stasiun Taiyō大洋駅Stasiun Taiyō pada Maret 2008LokasiKumiage 2676-3, Hokota-she, Ibaraki-ken 311-2103JepangKoordinat36°06′31″N 140°34′34″E / 36.1085°N 140.5762°E / 36.1085; 140.5762Koordinat: 36°06′31″N 140°34′34″E / 36.1085°N 140.5762°E / 36.1085; 140.5762Operator Kashima Rinkai TetsudoJalur■ Jalur Ōarai-KashimaLetak39.0 km dari MitoJumlah peron1 peron pulauLayanan Terminal bus Informasi lainStatusTanpa stafSitu...

Université de Londres

Université de LondresSenate House, siège de l'universitéHistoireFondation 1836StatutType Université fédéraleNom officiel University of LondonDirecteur Wendy ThomsonMembre de Jisc (en), Digital Preservation Coalition (en), Association des universités européennesSite web www.london.ac.ukChiffres-clésÉtudiants 170 000[1]LocalisationPays Royaume-UniVille Londresmodifier - modifier le code - modifier Wikidata Senate House, siège de l'université de Londres. Le premier bâtiment de l'uni...

Macleaya cordata

Species of plant Macleaya cordata Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Eudicots Order: Ranunculales Family: Papaveraceae Genus: Macleaya Species: M. cordata Binomial name Macleaya cordata(Willd.) R.Br. Synonyms Bocconia cordata Willd. Macleaya cordata, the five-seeded plume-poppy,[1] is a species of flowering plant in the poppy family Papaveraceae,[2] which is used ornamentally.[3] It is native to China and Japa...

Lift (Shannon Noll song)

2005 single by Shannon Noll LiftSingle by Shannon Nollfrom the album Lift Released5 December 2005 (2005-12-05)[1]Length4:19LabelSony BMGSongwriter(s)Shannon Noll, Andrew Roachford, Bryon Jones, Adam ReilyProducer(s)Bryon Jones, Adam ReilyShannon Noll singles chronology Shine (2005) Lift (2005) Now I Run (2006) Lift is the second single by Australian singer Shannon Noll from his second album of the same name (2005). The song debuted at number 13 during the Christmas seas...

Mergosono massacre

1947 anti-Chinese massacre in Malang, East Java, Indonesia Mergosono massacrePart of the Indonesian National Revolution 200km124miles LocationMalang, East Java, Dutch East IndiesDate31 July 1947 (1947-07-31)Attack typemassacreDeaths30[1]VictimsChinese community of MergosonoPerpetratorsIndonesian revolutionaries vteIndonesian National Revolution1945 Bersiap Kotabaru Semarang Medan Ambarawa Surabaya Kolaka Cumbok Borneo West Kalimantan Kumai 1946 Lengkong East Sumat...

Slaad

Fictional Dungeons & Dragons monster This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Slaad – news · newspapers · books · scholar · JSTOR (December 2015) (Learn how and when to remove this message) SlaadFirst appearanceFiend Folio (1981)In-universe informationTypeOutsiderAlignmentChaotic neutral The slaad...

Walbridge A. Field

American judge Walbridge Abner FieldMember of the U.S. House of Representativesfrom Massachusetts's 3rd districtIn officeMarch 4, 1877 – March 28, 1878Preceded byHenry L. PierceSucceeded byBenjamin DeanIn officeMarch 4, 1879 – March 3, 1881Preceded byBenjamin DeanSucceeded byAmbrose RanneyAssociate Justice of the Massachusetts Supreme Judicial CourtIn officeFebruary 21, 1881 – September 4, 1890Appointed byJohn Davis LongPreceded bySeth AmesSucceede...

Jerry Yan

Jerry YanLahir廖洋震 / Liào Yángzhèn1 Januari 1977 (umur 47)Taoyuan, TaiwanPekerjaanaktor, penyanyiTahun aktif1993 - sekarangSitus webwww.starjerry.net Jerry Yan (Chinese: 言承旭; pinyin: Yán Chéngxù) (lahir 1 Januari 1977) adalah aktor asal Taiwan. Ia juga merupakan anggota F4. Ia memiliki nama asli Liao Yangzhen (Chinese: 廖洋震; pinyin: Liào Yángzhèn). Filmografi Film Tahun Judul Inggris Judul Mandarin Peran Catatan 2004 Magic Kitchen 魔幻厨房 Guo Keli 2012...

Fécamp Abbey

Benedictine abbey in Fécamp, Seine-MaritimeAbbey church, Fécamp The Abbey of the Holy Trinity at Fécamp, commonly known as Fécamp Abbey (French: Abbaye de la Trinité de Fécamp), is a Benedictine abbey in Fécamp, Seine-Maritime, Upper Normandy, France. The abbey is known as the first producer of bénédictine, a herbal liqueur based on brandy.[1] First foundation Around 658, Waningus, a Merovingian count, founded a nunnery here, which was destroyed by the Vikings in 841.[2&#...

Isabel Swan

Brazilian sailor You can help expand this article with text translated from the corresponding article in Portuguese. (May 2020) Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipedia. Consider adding a topic to this tem...

List of diplomatic missions of Panama

This article uses bare URLs, which are uninformative and vulnerable to link rot. Please consider converting them to full citations to ensure the article remains verifiable and maintains a consistent citation style. Several templates and tools are available to assist in formatting, such as reFill (documentation) and Citation bot (documentation). (August 2022) (Learn how and when to remove this message) Countries with Panamanian diplomatic missions The Republic of Panama's status as major flag...

نور هشام عبد الله

تان سري [لغات أخرى]‏ نور هشام عبد الله معلومات شخصية الميلاد 21 أبريل 1963 (61 سنة) سيبانغ [لغات أخرى]‏ مواطنة ماليزيا الحياة العملية المدرسة الأم الجامعة الوطنية الماليزية (الشهادة:دكتور في الطب) (–1988) المهنة مسؤول، وجراح اللغات المل�...

Andromache

Wife of Hector in Greek mythology Not to be confused with Andromeda (mythology). For other uses, see Andromache (disambiguation). Andromache Mourning Hector by Jacques-Louis David, 1783 In Greek mythology, Andromache (/ænˈdrɒməkiː/; Ancient Greek: Ἀνδρομάχη, Andromákhē [andromákʰɛ:]) was the wife of Hector, daughter of Eetion, and sister to Podes.[1] She was born and raised in the city of Cilician Thebe, over which her father ruled. The name means 'man batt...

Amenhotep II

Seventh Pharaoh of the Eighteenth dynasty of Egypt Amenhotep IIAmenophis IIAmenhotep II standing before Osiris.PharaohReign1427–1401 BC or 1427–1397 BCPredecessorThutmose IIISuccessorThutmose IVRoyal titulary Horus name Ka nakht wer pekhtykꜢ nḫt wr-pḥtyVictorious bull, great of might[1] Nebty name Weser fau, sekha em wasetwsr fꜢw sḫꜤi m wꜢstRich in splendor, who has been made to appear in Thebes[1] Golden Horus Ity sekhem.ef em tau nebuiṯi sḫm.f m...

Lord of the manor

Landholder of a rural estate For other uses, see Lord of the manor (disambiguation) and Lady of the manor (disambiguation). Ightham Mote, a 14th-century moated manor house near Sevenoaks, Kent, England English feudalismHarold Sacramentum Fecit Willelmo Duci(Bayeux Tapestry) FiefEcclesiastical fiefCrown landAllodial titleAppanageVassalFeoffmentSeignorySubinfeudationFeoffeeFealtyHomageAffinityFeudal maintenanceFeudal fragmentationBastard feudalismLivery Manorialism Lord of the manorManorial cou...

一中同表

一中同表，是台灣处理海峡两岸关系问题的一种主張，認為中华人民共和国與中華民國皆是“整個中國”的一部份，二者因為兩岸現狀，在各自领域有完整的管辖权，互不隶属，同时主張，二者合作便可以搁置对“整个中國”的主权的争议，共同承認雙方皆是中國的一部份，在此基礎上走向終極統一。最早是在2004年由台灣大學政治学教授張亞中所提出，希望兩岸由一中各表�...

Jon Bon Jovi

American rock musician (born 1962) Jon Bon JoviBon Jovi in 2012BornJohn Francis Bongiovi Jr. (1962-03-02) March 2, 1962 (age 62)Perth Amboy, New Jersey, U.S.EducationSt. Joseph High SchoolSayreville War Memorial High SchoolOccupations Singer songwriter musician actor Years active1975–presentSpouse Dorothea Hurley (m. 1989)Children4, including JakeRelatives Tony Bongiovi (cousin) Robert Hegyes (cousin) Millie Bobby Brown (daughter-in-law) Musical care...

Alison Drennan

Australian rules footballer Australian rules footballer Alison Drennan Drennan in May 2019Personal informationDate of birth (1991-01-30) 30 January 1991 (age 33)Original team(s) Southern Saints (VFLW)Debut Round 1, 2019, North Melbourne vs. Carlton, at North Hobart OvalHeight 176 cm (5 ft 9 in)Position(s) MidfielderClub informationCurrent club West CoastPlaying career1Years Club Games (Goals)2019 North Melbourne 07 (1)2020 St Kilda 05 (0)2021–2023 Gold Coast 40...

National Institute for Space Research

Brazilian space technology organization This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: National Institute for Space Research – news · newspapers · books · scholar · JSTOR (September 2019) (Learn how and when to remove this message) National Institute for Space ResearchInstituto Nacional de Pesquisas Espacia...

Square lattice

2-dimensional integer lattice Square lattices Upright squareSimple diagonal squareCentered Upright square tiling. The vertices of all squares together with their centers form an upright square lattice. For each color the centers of the squares of that color form a diagonal square lattice which is in linear scale √2 times as large as the upright square lattice. In mathematics, the square lattice is a type of lattice in a two-dimensional Euclidean space. It is the two-dimensional version of t...

/profillengkap.com/index.php/article/Colorado Western Slope

Trans Jateng

/profillengkap.com/index.php/article/Robin Jenkins

Dil Chahta Hai

Eryngium

Komando Resor Militer 051

Bahasa Menominee

Kalaripayattu

Renaud Jay

Daftar permainan video di Museum of Modern Art

Buncis

Fox Entertainment