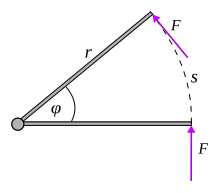
Công (vật lý học)
| |||||||||||||||||||||||||||||
Read other articles:

This article is about the city in Germany. For other uses, see Marburg (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Marburg – news · newspapers · books · scholar · JSTOR (August 2013) (Learn how and when to remove this template message) Town in Hesse, GermanyMarburg TownView of Marburg, ...

Bendungan biwara di Algonquin Park, Ontario, Kanada Bendungan biwara atau kolam biwara adalah bendungan yang dibangun oleh biwara untuk membuat kolam sebagai tempat perlindungan dari para predator seperti koyote, serigala dan beruang, serta untuk tempat penyimpanan makanan pada musim dingin. Struktur bendungan ini memodifikasi lingkungan alam sedemikian rupa sehingga keseluruhan ekosistem yang telah ada mengalami perubahan. Hal ini menjadikan biwara sebagai spesies kunci. Pranala luar Wikimed...

Sanggraloka menggabungkan sebuah hotel dan berbagai rekreasi, seperti kolam renang. Sanggraloka atau resor (bahasa Inggris: resort) adalah tempat untuk relaksasi atau rekreasi, menarik pengunjung untuk berlibur. Sanggraloka juga tempat, kota atau kadang-kadang bangunan komersial yang dioperasikan oleh suatu perusahaan. Sanggraloka sendiri menyediakan banyak keinginan pengunjung seperti makanan, minuman, penginapan, olahraga, hiburan, dan perbelanjaan. Sebutan sanggraloka kadang-kadang salah d...

Deinococcus radiodurans Bentuk tetrad Deinococcus radiodurans dilihat menggunakan mikroskop transmisi elektron (TEM) Klasifikasi ilmiah Domain: Bacteria Filum: Deinococci Ordo: Deinococcales Famili: Deinococcuceae Genus: Deinococcus Spesies: D. radiodurans Nama binomial Deinococcus radioduransBrooks & Murray, 1981 [1] Deinococcus radiodurans adalah salah satu bakteri kelompok ekstremofil (dapat hidup di suasana ekstrem) dengan karakteristik utama berupa ketahanan terhadap ef...

Untuk orang lain dengan nama yang sama, lihat Michael Griffin. Michael D. Griffin Menteri Tingkat Rendah Pertahanan untuk Riset dan TeknikMasa jabatan19 Februari 2018 – 10 Juli 2020PresidenDonald Trump PendahuluJabatan dibentukPenggantiMichael Kratsios (pelaksana tugas)Administrator Badan Penerbangan dan Antariksa Amerika Serikat ke-11Masa jabatan13 April 2005 – 20 Januari 2009PresidenGeorge W. BushWakilShana Dale PendahuluSean O'KeefePenggantiCharles Bolden Informasi pr...

Filoktetes di Pulau Lemnos (1788) oleh Jean Germain Drouais. Filoktetes (bahasa Yunani Kuno: Φιλοκτήτης, translit. Philoktētēs) dalam mitologi Yunani adalah putra raja Poias dari Meliboia, Thessalia. Dia adalah seorang pahlawan Yunani yang terkenal karena keterlibatannya dalam Perang Troya. Kisahnya menjadi tema dalam setidaknya dua sandiwara oleh Sofokles, salah satunya berjudul namanya sendiri, serta dua drama lainnya masing-masing oleh Aiskhilos dan Euripides. Akan tet...

Form of megalithic tomb Gallery grave, missing a portion of its tumulus and all its stone caps, in a cemetery in Herrljunga, Sweden. A gallery grave is a form of megalithic tomb built primarily during the Neolithic Age[1] in Europe in which the main gallery of the tomb is entered without first passing through an antechamber or hallway.[1][2][3] There are at least four major types of gallery grave (complex, transepted, segmented, and wedge-shaped), and they may ...

Untuk kegunaan lain, lihat Pulang (disambiguasi). PulangGenre Drama Roman SkenarioNataya BagyaCeritaMonty TiwaSutradaraSergi SutantoPemeran Della Dartyan Cok Simbara Ira Wibowo Dwi Sasono Rangga Nattra Lagu pembukaPulang oleh Kevin WidayaLagu penutupPulang oleh Kevin WidayaPenata musikAndi RiantoNegara asalIndonesiaBahasa asliBahasa IndonesiaJmlh. musim1Jmlh. episode6ProduksiProduser eksekutif Monika Rudijono Tina Arwin Indra Yudhistira Produser Tia Hendani Sumarsono SinematografiKoko K...

Северный морской котик Самец Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапси...

艾德礼伯爵 阁下The Rt Hon. The Earl AttleeKG OM CH PC FRS联合王国首相任期1945年7月26日—1951年10月26日君主乔治六世副职赫伯特·莫里森前任温斯顿·丘吉尔继任温斯顿·丘吉尔联合王国副首相任期1942年2月19日—1945年5月23日(战时内阁)君主乔治六世首相温斯顿·丘吉尔前任职位创立继任赫伯特·莫里森反对党领袖任期1951年10月26日—1955年11月25日君主乔治六世伊丽莎白二�...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Idola Kecil – berita · surat kabar · buku · cendekiawan · JSTOR Idola KecilPresenterZizan Razak Alif SatarNegara asalMalaysiaJmlh. musim5Jmlh. episodevariasiProduksiDurasi60 menitRilis asliJaringanTV9For...

City in Washington, United States City in Washington, United StatesOcean ShoresCityOcean Shores main entranceLocation of Ocean Shores, WashingtonCoordinates: 46°58′18″N 124°9′17″W / 46.97167°N 124.15472°W / 46.97167; -124.15472CountryUnited StatesStateWashingtonCountyGrays HarborFounded1970IncorporatedNovember 3, 1970Government • TypeCouncil–manager • MayorFrank Eluden[1]Area[2] • Total13.78 sq ...

Fringe theory that the Armenian genocide did not occur The Iğdır Genocide Memorial and Museum promotes the view that Armenians committed genocide against Turks, rather than vice versa.[1] Armenian genocide denial is the claim that the Ottoman Empire and its ruling party, the Committee of Union and Progress (CUP), did not commit genocide against its Armenian citizens during World War I—a crime documented in a large body of evidence and affirmed by the vast majority of scholars...

2003 live album by The WhoThe Who Live at the Royal Albert HallLive album by The WhoReleasedJune 2003Recorded27 November 2000 and 8 February 2002VenueRoyal Albert Hall, City of Westminster, London, England, United KingdomGenreRockLength161:57LabelSteamhammerDirectorDick CarruthersProducerBob PriddenThe Who chronology The Ultimate Collection(2002) The Who Live at the Royal Albert Hall(2003) Then and Now(2004) Professional ratingsReview scoresSourceRatingThe Encyclopedia of Popular Mus...

Aspect of Carlist history Carlist standard During 40 years of post-Francoist Spain there have been some 200 works published on Carlist history during the Franco regime (1939 to 1975; the Civil War period is not discussed here); there are some 100 authors who have contributed. The number of major studies – books or unpublished PhD works - stands at around 50, the rest are articles in specialized reviews (pieces in popular newspapers or periodicals are not acknowledged here). Except some 15 t...

American judge (born 1974) Tom KleehChief Judge of the United States District Court for the Northern District of West VirginiaIncumbentAssumed office March 19, 2022Preceded byGina M. GrohJudge of the United States District Court for the Northern District of West VirginiaIncumbentAssumed office November 5, 2018Appointed byDonald TrumpPreceded byIrene Patricia Murphy Keeley Personal detailsBorn (1974-09-14) September 14, 1974 (age 49)Wheeling, West Virginia, U.S.EducationWest Virgi...

هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (يناير 2022) هذه الم...

Questa voce sugli argomenti valute e Isola del Principe Edoardo è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Dollaro dell'Isola del Principe Edoardofuori corsoNome localePrince Edward Island dollar Codice ISO 4217- Stati Isola del Principe Edoardo Simbolo$ Frazionicent (1/100) Monete1 cent Banconote1, 2, 5, 10, 20 $ Periodo di circolazione1871 - 1873 Sostituita dadollaro canadese dal 1873 Tasso di cambio() Lista valute ISO 4217 -...

Bupati AgamPetahanaAndri Warmansejak 26 Februari 2021KediamanRumah Dinas Bupati AgamDibentuk8 Oktober 1945 (di bawah pemerintahan Indonesia)Pejabat pertamaMuhammad Djosan St. Bidjo RadjoSitus webwww.agamkab.go.id Bupati Agam adalah politisi yang dipilih untuk bertanggung jawab dalam mengatur dan mengelola pemerintahan Kabupaten Agam, sebagai bagian dari sistem penyelenggaraan pemerintahan daerah di Indonesia. Setelah proklamasi kemerdekaan Indonesia, Muhammad Djosan St. Bidjo Radjo diang...

جزء من سلسلة حولالماركسية مؤلفات نظرية المخطوطات الاقتصادية والفلسفية (1844) أطروحات حول فويرباخ الأيديولوجية الألمانية بيان الحزب الشيوعي برومير الثامن عشر للويس بونابرت غرندريسه مساهمة في نقد الاقتصاد السياسي رأس المال جدليات الطبيعة مفاهيم اشتراكية علمية حتمية اقتصاد...