Read other articles:

Coleen RooneyRooney in a branch of T for TelecomLahirColeen Mary McLoughlin03 April 1986 (umur 37)Liverpool, Merseyside, InggrisTempat tinggalPrestbury, CheshireKebangsaanInggrisNama lainColeen McLoughlinPendidikanSt John Bosco Arts CollegePekerjaanPresenter televisi, kolumnisSuami/istriWayne Rooney ​(m. 2008)​Anak3 Coleen Mary Rooney (née McLoughlin; lahir 3 April 1986) adalah seorang presenter televisi Inggris, kolumnis dan selebriti endorser produk ...

Эту статью предлагается удалить.Пояснение причин и соответствующее обсуждение вы можете найти на странице Википедия:К удалению/4 сентября 2022.Пока процесс обсуждения не завершён, статью можно попытаться улучшить, однако следует воздерживаться от переименований или нем�...

Joie DavidowBornPhiladelphia, Pennsylvania, U.S.EducationUniversity of Pennsylvania (BA)New England Conservatory of Music (Master of Music)Occupation(s)Author, EditorKnown forco-founder of LA Weekly Joie Davidow is an author and editor best known as co-founder of LA Weekly and L.A. Style magazines, and for her memoir Marked for Life. Early life and education Davidow was born in Philadelphia, United States, to a Romanian Jewish mother and Russian Jewish father.[1] She grew up in t...

Train in India Dadar–Sainagar Shirdi Superfast ExpressOverviewService typeSuperfast ExpressLocaleMaharashtraFirst service28 August 2010Current operator(s)Central RailwaysRouteTerminiDadarSainagar ShirdiStops8Distance travelled336 km (209 mi)Average journey time6 hoursService frequencyTri-weeklyTrain number(s)12131 / 12132On-board servicesClass(es)AC 2 tier, AC 3 tier, Sleeper class, General UnreservedSeating arrangementsYesSleeping arrangementsYesCatering facilitiesNot availableOb...

2016 book by Michael Leahy The Last Innocents:The Collision of the Turbulent Sixties and the Los Angeles Dodgers AuthorMichael LeahyCountryUnited StatesLanguageEnglishGenreNon-fictionPublisherHarperCollinsPublication dateMay 10, 2016ISBN978-0-06-236056-4 The Last Innocents: The Collision of the Turbulent Sixties and the Los Angeles Dodgers is a book by author Michael Leahy, centered around the Los Angeles Dodgers teams of the 1960s. The book was the winner of the 2016 Casey Award as the best ...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府（Oguzkhan Presidential Palace）機關所在地阿什哈巴德任命者直接选举任期7年，可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關（英语：National Council of Turkmenistan） ...

Online travel agency platform Omio GmbHCompany typeTravel websiteFounded2013; 11 years ago (2013)FounderNaren ShaamHeadquartersBerlin, GermanyWebsiteomio.com GoEuro Travel GmbH, doing business as Omio, formerly known as GoEuro, is a German online travel comparison and booking website based in Berlin, Germany.[1] It was founded in 2013 as GoEuro by Naren Shaam.[2][3] Omio employs more than 300 people and is active in 37 countries globally.[4] T...

Egyptian pharaoh (First Dynasty) Hor-AhaAha Menes(?)Faience vessel fragment with serekh inscribed with the Horus-name Aha, on display at the British Museum.PharaohReign31st century BCPredecessorNarmerSuccessorDjerRoyal titulary Horus name Hor-AhaḤrw-ꜥḥꜣHorus, the fighter Nomen Tetittj ConsortBenerib, KhenthapChildrenDjerFatherNarmer ?BurialChambers B10, B15, B19, Umm el-Qa'abDynasty1st Dynasty Hor-Aha (or Aha or Horus Aha) is considered the second pharaoh of the First Dynasty of ...

M156 redirects here. For other uses, see M156 (disambiguation). Reciprocating internal combustion engine Mercedes-Benz M156/M159OverviewManufacturerMercedes-AMGLayoutConfigurationNaturally aspirated 90° V8Displacement6.2 L (6,208 cc)Cylinder bore102.2 mm (4.02 in)Piston stroke94.6 mm (3.72 in)ValvetrainDOHC 4 valves x cyl.Compression ratio11.3:1RPM rangeMax. engine speed7,250-8,000CombustionFuel systemFuel injectionFuel typeGasolineOil systemM156: Wet sumpM159: ...

County in Florida, United States Volusia redirects here. For the unincorporated community, see Volusia, Florida. For the moth, see Peoria (moth). County in FloridaVolusia CountyCountyVolusia County courthouse in DeLand, built in 2001 LogoLocation within the U.S. state of FloridaFlorida's location within the U.S.Coordinates: 29°3′N 81°9′W / 29.050°N 81.150°W / 29.050; -81.150Country United StatesState FloridaFoundedDecember 29, 1854Named forCommunity o...

منتخب تايبيه الصينية لكرة القدم معلومات عامة بلد الرياضة  تايوان الفئة كرة القدم للرجال  رمز الفيفا TPE  الاتحاد اتحاد تايبيه الصينية لكرة القدم كونفدرالية آفك (آسيا) الملعب الرئيسي ملعب كاوهسيونغ الوطني الموقع الرسمي الموقع الرسمي  الطاقم واللاعبون المدرب غاري ...

Wrestling event 2024 Asian Wrestling ChampionshipsHost city Bishkek, KyrgyzstanDates11–16 April 2024StadiumBishkek ArenaChampionsFreestyle IranGreco-Roman IranWomen Japan← 20232025 → The 2024 Asian Wrestling Championships is the 20th edition of Asian Wrestling Championships of combined events, and took place from 11 to 16 April in Bishkek, Kyrgyzstan.[1][2] Competition schedule All times are (UTC+6) Date Time Event 11 April 11.00-13.30 Q...

American actress (1910–2006) Not to be confused with Jane Wyman. Jane WyattWyatt in the 1930sBornJane Waddington Wyatt(1910-08-12)August 12, 1910Franklin Lakes, New Jersey, U.S.DiedOctober 20, 2006(2006-10-20) (aged 96)Los Angeles, California, U.S.Alma materBarnard CollegeOccupationActressYears active1931–1996Spouse Edgar Bethune Ward ​ ​(m. 1935; died 2000)​Children3AwardsEmmy Award (1958, 1959, 1960) Jane Waddington Wyatt (/...

Questa voce sull'argomento società di pallacanestro francesi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Stade Philippin omnisports Rouen BasketPallacanestro Segni distintiviUniformi di gara Casa Trasferta Colori sociali Bianco e blu Dati societariCittàRouen Nazione Francia ConfederazioneFIBA Europe FederazioneFFBB CampionatoPro B Fondazione1998 DenominazioneStade Philippin omnisports Rouen Basket(1998-presente) ImpiantoSalle des Cotonniers...

「東ドイツ」はこの項目へ転送されています。二度の世界大戦でドイツが失った、本項で述べられているドイツ民主共和国よりさらに東の領土については「旧ドイツ東部領土」をご覧ください。 ドイツ民主共和国 Deutsche Demokratische Republik (ドイツ語) ← ← 1949年 - 1990年 → （国旗） （国章） 国の標語: „Proletarier aller Länder, vereinigt Euch!“（ドイツ語）万国の労働者よ...

50th season of Europe's secondary club football tournament organised by UEFA 2020–21 UEFA Europa LeagueThe Stadion Gdańsk in Gdańsk hosted the finalTournament detailsDatesQualifying:18 August 2020 – 1 October 2020Competition proper:22 October 2020 – 26 May 2021TeamsCompetition proper: 48+8Total: 158+55 (from 55 associations)Final positionsChampions Villarreal (1st title)Runners-up Manchester UnitedTournament statisticsMatches played204Goals scored618 (3.03 per match)Att...

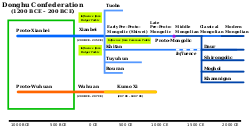
Official language of Mongolia Mongolianмонгол хэлᠮᠣᠩᠭᠣᠯ ᠬᠡᠯᠡ MongolPronunciation[ˈmɔɴ.ɢəɮ xiɮ]Native toMongolian PlateauRegionAll of Mongolia, Inner Mongolia, Buryatia, Kalmykia; parts of Irkutsk Oblast, Zabaykalsky Krai in Russia; parts of Liaoning, Jilin, Heilongjiang, Xinjiang, Gansu and Qinghai provinces in China; Issyk-Kul Region in KyrgyzstanEthnicityMongols, BuryatsNative speakers(6.2 million cited 1982–2020)[1]Language familyM...

Extremely large or complex datasets This article is about large collections of data. For the band, see Big Data (band). For the practice of buying and selling of personal and consumer data, see Surveillance capitalism. Non-linear growth of digital global information-storage capacity and the waning of analog storage[1][needs update] Big data primarily refers to data sets that are too large or complex to be dealt with by traditional data-processing application software. Data wit...

この項目では、鹿児島県の企業について説明しています。茨城県の企業については「タイヨー (茨城県)」をご覧ください。 株式会社タイヨー>[広報 1]Taiyo Co., Ltd. タイヨー本社種類 株式会社市場情報 非上場(以下は過去のデータ)東証2部 99492013年7月16日[広報 1] - 2013年11月27日[広報 1] 大証2部（廃止） 99491994年7月28日[広報 1] - 2013年7月12日 福証 9949...

Camille Jordan, auteur du théorème clé de la théorie En mathématiques et plus précisément en algèbre non commutative, un module sur un anneau est dit semi-simple ou complètement réductible s'il est somme directe de sous-modules simples ou, ce qui est équivalent, si chacun de ses sous-modules possède un supplémentaire. Les propriétés des modules semi-simples sont utilisées en algèbre linéaire pour l'analyse des endomorphismes, dans le cadre des anneaux semi-simples et pour la...