Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. Yuto Miyazawa宮澤佑門Nama lahirYuto MiyazawaLahir21 Februari 2000 (umur 24)Tokyo, JepangGenreRock, hard rock, heavy metalPekerjaanMusikusInstrumenGitar, vokalTahun aktif2008–sekarangLabelRelixArtis terkaitThe RobotixSitus webhttp://www.yutog...

Carlo SalottiPrefek Kongregasi bagi RitusSalotti pada sekitar tahun 1939.GerejaGereja Katolik RomaPenunjukan14 September 1938Masa jabatan berakhir24 Oktober 1947PendahuluCamillo LaurentiPenerusGaetano CicognaniJabatan lainKardinal-Uskup Palestrina (1939-47)ImamatTahbisan imam22 September 1894Tahbisan uskup6 Juli 1930oleh Wilhelmus Marinus van RossumPelantikan kardinal13 Maret 1933 (in pectore)16 Desember 1935 (diumumkan)oleh Paus Pius XIPeringkatKardinal-Imam (1935-39)Cardinal-Bishop (19...

Untuk aktris Inggris, lihat Anna Shaffer. SantoAnna SchäfferMystic, StigmatistLahir(1882-02-18)18 Februari 1882Mindelstetten, Bavaria, Kekaisaran JermanMeninggal5 Oktober 1925(1925-10-05) (umur 43)Mindelstetten, Bavaria, GermanyDihormati diKatolik RomaBeatifikasi7 Maret 1999, Saint Peter's Basilica, Kota Vatikan oleh Paus John Paul IIKanonisasi21 Oktober 2012, Vatican City oleh Paus Benedict XVI[1]Pesta5 Oktober (Katolik Roma) Bagian dari seri tentangMistisisme Kristiani Teologi...

Ular Bangkai laut Ular bangkai laut, Trimeresurus albolabris Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Subfilum: Vertebrata Kelas: Reptilia Ordo: Squamata Subordo: Serpentes Famili: Viperidae Subfamili: Crotalinae Genus: Trimeresurus Spesies: T. albolabris Nama binomial Trimeresurus albolabrisGray, 1842 Ular bangkai laut biasa juga dikenal dengan sebutan viper Hijau adalah sejenis ular berbisa yang berbahaya. Memiliki nama ilmiah Trimeresurus albolabris, ular ini juga dikena...

History of Indian state of Bihar The Maurya Empire with capital at Patliputra spanned across the Indian subcontinent as well as over parts of modern-day Iran and modern-day Myanmar. History of South Asia Outline Palaeolithic (2,500,000–250,000 BC) Madrasian culture Soanian culture Neolithic (10,800–3300 BC) Bhirrana culture (7570–6200 BC) Mehrgarh culture (7000–3300 BC) Edakkal culture (5000–3000 BC) Chalcolithic (3500–1500 BC) Anarta tradition (c. 3950–1900 BC) Ahar-Banas...

Voce principale: Pandemia. Corsia dell'Ospedale di Camp Funston nel Kansas durante l'influenza spagnola del 1918 Una pandemia influenzale è un'epidemia di virus influenzale che si espande su scala mondiale e infetta una grande porzione della popolazione umana. A differenza delle regolari epidemie stagionali le pandemie avvengono irregolarmente, e ne compaiono circa 3 in ogni secolo[1]. Il fatto che sia dichiarata pandemia non vuol dire che sia una patologia grave, dato che tale defi...

追晉陸軍二級上將趙家驤將軍个人资料出生1910年 大清河南省衛輝府汲縣逝世1958年8月23日(1958歲—08—23)（47—48歲） † 中華民國福建省金門縣国籍 中華民國政党 中國國民黨获奖 青天白日勳章（追贈）军事背景效忠 中華民國服役 國民革命軍 中華民國陸軍服役时间1924年－1958年军衔 二級上將 （追晉）部队四十七師指挥東北剿匪總司令部參謀長陸軍�...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Wasserkuppe – news · newspapers · books · scholar · JSTOR (April 2016) (Learn how and when to remove this template message) Mountain in Germany WasserkuppeHighest pointElevation950.2 m above sea level (NN) (3,117 ft)Prominence585 m...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています（詳細）。 数字の大字（だいじ）は、漢数字の一種。通常用いる単純な字形の漢数字（小字）の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券（「壱」が大字） 弐千円日本銀行券（「弐」が大字） 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题，请协助参考外语维基百科扩充条目。请勿直接提交机械翻译，也不要翻译不可靠、低品质内容。依版权协议，译文需在编辑摘要注明来源，或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌：《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

British retail company The Flannels Group LimitedTrade nameFlannelsFormerlyCleverjoin Limted (1988–2000)[1]Company typePrivateIndustryRetailFounded1976; 48 years ago (1976)FounderNeil ProsserHeadquartersLondon, United KingdomNumber of locations50+ProductsClothingFootwearAccessoriesServicesFlannels Elite+Flannels RentalNumber of employees700 (2024)ParentSportsdirect.com Retail Limited[2][a]Websiteflannels.com The Flannels Group Limited, trading as Fl...

Cet article est une ébauche concernant une localité tunisienne. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Kalâa Kebira Vue sur Kalâa Kebira. Administration Pays Tunisie Gouvernorat Sousse Délégation(s) Kalâa Kebira Démographie Population 53 323 hab. (2014[1]) Densité 4 761 hab./km2 Géographie Coordonnées 35° 52′ 15″ nord, 10° 32′ 07″ es...

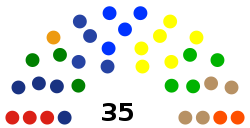
Dewan Perwakilan Rakyat Daerah Kabupaten Kuantan SingingiDewan Perwakilan RakyatKabupaten Kuantan Singingi2019-2024JenisJenisUnikameral Jangka waktu5 tahunSejarahSesi baru dimulai9 September 2019PimpinanKetuaDr. Adam, S.H., M.H. (Golkar) sejak 25 Februari 2021 Wakil Ketua IZulhendri Nazaruddin, S.T. (PPP) sejak 2 Oktober 2019 Wakil Ketua IIJuprizal, S.E., M.Si. (Gerindra) sejak 2 Oktober 2019 KomposisiAnggota35Partai & kursi  PDI-P (3)   NasDem (4)  &#...

Yangtze River Express金鹏航空 IATA ICAO Kode panggil Y8 YZR YANGTZE RIVER Didirikan15 Januari 2003PenghubungBandar Udara Internasional Pudong ShanghaiArmada14Kantor pusatShanghai, Republik Rakyat TiongkokSitus webhttp://www.yzr.com.cn/ Yangtze River Express Boeing 747-481 Yangtze River Express (Yangtze River Express Airlines Company Limited) (扬子江快运航空公司 atau 扬子江快运) adalah nama maskapai penerbangan kargo yang berbasis di Shanghai, Republik Rakyat Tiongkok. Sejara...

American football player (born 1992) American football player Hau'oli KikahaNo. 45, 44Position:LinebackerPersonal informationBorn: (1992-07-24) July 24, 1992 (age 31)Hauʻula, Hawaii, U.S.Height:6 ft 3 in (1.91 m)Weight:246 lb (112 kg)Career informationHigh school:Kahuku (Kahuku, Hawaii)College:WashingtonNFL draft:2015 / Round: 2 / Pick: 44Career history New Orleans Saints (2015–2017) Dallas Renegades (2020) Career highlights and awards Unan...

Japanese philosopher Miyake SetsureiMiyake SetsureiBornJuly 7, 1860Kanazawa, Ishikawa, Japan[1]DiedNovember 26, 1945(1945-11-26) (aged 85)OccupationPhilosopher, author, journalistGenrePolitics, culture Part of a series onConservatism in Japan Ideologies Capitalist Fiscal State Corporate  Nationalist Minzoku Populist Shōwa Statism Ultra Neo Paternalistic Religious State Shinto Ultra Principles Anti-communism Asian values Authority Bushido Discipline Duty Elitism Aristocracy ...

Queen of France from 1615 to 1644 This article is about the queen consort. For other women named Anne of Austria, see Anna of Austria (disambiguation). Anne of AustriaInfanta of SpainPortrait by Peter Paul Rubens, c. 1620sQueen consort of FranceTenure24 November 1615 – 14 May 1643Queen consort of NavarreTenure24 November 1615 – 20 October 1620Queen regent of FranceRegency14 May 1643 – 7 September 1651MonarchLouis XIVBorn(1601-09-22)22 September 1601Benavente Palace, Valladolid, Cr...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (يناير 2018) الدوري البحريني الممتاز 1975–76معلومات عامةالرياضة كرة القدم البطولة الدوري الب...

Imperial Japanese Navy ship For other ships with the same name, see List of ships named Yamato. Yamato undertaking sea trials in the Bungo Channel, 20 October 1941 History Empire of Japan NameYamato NamesakeYamato Province, and an archaic name for Japan OrderedMarch 1937 BuilderKure Naval Arsenal Laid down4 November 1937 Launched8 August 1940 Commissioned16 December 1941 Stricken31 August 1945[1] FateSunk by American planes during Operation Ten-Go, 7 April 1945 General characteristics...

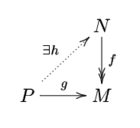
In matematica, un modulo proiettivo è un modulo con la proprietà di essere addendo diretto di un modulo libero: ovvero P è proiettivo se esiste un modulo libero F e un suo sottomodulo N tale che F è la somma diretta di P ed N. Questo concetto è il duale di quello di modulo iniettivo; è stato introdotto da Henri Cartan e Samuel Eilenberg nel 1956. Indice 1 Definizioni equivalenti 2 Esempi e proprietà 3 Risoluzioni proiettive 4 Note 5 Bibliografia 6 Collegamenti esterni Definizioni equiv...