Рівняння Дірака
| |||||||||||||||||||||||||||||
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Eduardo Gadiano Gubernur Mindoro BaratPetahanaMulai menjabat 30 Juni 2019PresidenRodrigo Duterte PendahuluMario Gene MendiolaPenggantiPetahanaWalikota SablayanMasa jabatan2010–2019 PendahuluGodofredo B. MintuPenggantiAndres D. Dangeros Informasi ...

American comic book writer and artist (born 1946) Walt SimonsonSimonson at the Big Apple Summer Sizzler, June 13, 2009BornWalter Simonson (1946-09-02) September 2, 1946 (age 77)Knoxville, Tennessee, U.S.NationalityAmericanArea(s)Writer, ArtistNotable worksThorFantastic FourDetective Comics (Manhunter)Metal MenStar SlammersOrionStar WarsX-FactorAwardsShazam Award: Outstanding New Talent (1973) Best Individual Short Story (Dramatic) (1973, with Archie Goodwin) Best Individual Short Story (...

10th Minnesota Infantry Regiment10th Minnesota Infantry Regiment Battle FlagActiveAugust 12, 1862 – August 28, 1865DisbandedAugust 28, 1865Country United StatesAllegianceUnionBranchInfantrySizeRegimentEngagementsAmerican Civil War Dakota War of 1862 Battle of Fort Ridgely Battle of New Ulm Battle of Acton Attack on Hutchinson Battle of Wood Lake Sibley's Expedition Against the Sioux Battle of Big Mound Battle of Dead Buffalo Lake Battle of Stony Lake Forrest's Defense of Mississippi Ba...

Miss IndonesiaLogo Miss IndonesiaTanggal pendirian2005TipeKontes kecantikanKantor pusat JakartaLokasi IndonesiaJumlah anggota Miss World(2006-sekarang)Miss ASEAN (2005)Bahasa resmi IndonesiaChairwoman and FounderLiliana TanoesoedibjoTokoh pentingMartha TilaarWulan TilaarLina PriscillaSitus webwww.missindonesia.co.id Miss Sumatera Selatan adalah sebuah gelar yang didapat bagi perwakilan provinsi Sumatera Selatan di ajang Miss Indonesia, dan pemegang titel saat ini adalah Audra Nabila Kasa...

Internazionali Femminili di Palermo 2013Doppio Sport Tennis Vincitori Kristina Mladenovic Katarzyna Piter Finalisti Karolína Plíšková Kristýna Plíšková Punteggio 6-1, 5-7, [10-8] Tornei Singolare Singolare (q) Doppio Doppio 2012 2014 Voce principale: Internazionali Femminili di Palermo 2013. Il doppio dell'Internazionali Femminili di Palermo 2013 è stato un torneo di tennis facente parte del WTA Tour 2013. Renata Voráčová e Barbora Záhlavová-Strýcová erano le detentric...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. Logo Kampanye Memeluk Ukraina. Memperkuat Persatuan. Merangkul Ukraina, Memperkuat Persatuan (Bahasa Inggris: Embrace Ukraine, Strengthen the Union; Bahasa Ukrainia: Прийми Україну. Зміцни Союз atau Pryimy Ukrainu. Zmitsny Soiuz)...

The 2008 Clemson Tigers team taking the field at Memorial Stadium. The Clemson Tigers college football team competes as part of the National Collegiate Athletic Association (NCAA) Division I Football Bowl Subdivision, representing Clemson University in the Atlantic Division of the Atlantic Coast Conference (ACC). Clemson has played their home games at Memorial Stadium in Clemson, South Carolina since 1942.[1] The Tigers have three national championship titles (1981, 2016 and 2018) al...

Pakistani Baloch separatist and militant leader Dr. Allah Nazar BalochDr. Allah Nazar Balochi in left with Aslam Baloch in right sideNative nameاللہ نذر بلوچBorn2 October 1968[1]RankLeaderCommands heldBaloch Liberation Front (BLF)Battles/warsInsurgency in BalochistanSpouse(s)Fazela Baloch[2] Dr. Allah Nazar Baloch (Urdu: اللہ نذر بلوچ, Balochi: الله نذر بلۏچ), is the current leader of Baloch Liberation Front (BLF), a militant group operating in...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (نوفمبر 2017) الخطوط الجوية الجنوبية العليا إياتا إيكاو رمز النداء؟؟ تاريخ الإنشاء 2013 الجنسية جنوب السودان موقع ويب الموقع الرسمي تعديل مصدري - تعديل ا�...

Військово-музичне управління Збройних сил України Тип військове формуванняЗасновано 1992Країна Україна Емблема управління Військово-музичне управління Збройних сил України — структурний підрозділ Генерального штабу Збройних сил України призначений для планува...

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

العلاقات الإيطالية الليبيرية إيطاليا ليبيريا إيطاليا ليبيريا تعديل مصدري - تعديل العلاقات الإيطالية الليبيرية هي العلاقات الثنائية التي تجمع بين إيطاليا وليبيريا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه ال...

American college football season 2008 California Golden Bears footballEmerald Bowl championEmerald Bowl, W 24–17 vs. Miami (FL)ConferencePacific-10 ConferenceRankingCoachesNo. 25Record9–4 (6–3 Pac-10)Head coachJeff Tedford (7th season)Offensive coordinatorFrank Cignetti Jr. (1st season)Offensive schemePro-styleDefensive coordinatorBob Gregory (7th season)Base defense4–3Home stadiumCalifornia Memorial Stadium(Capacity: 71,799)Seasons← 20072...

Iyokan Iyokan Klasifikasi ilmiah Kerajaan: Plantae (tanpa takson): Angiospermae (tanpa takson): Eudikotil (tanpa takson): Rosid Ordo: Sapindales Famili: Rutaceae Genus: Citrus Spesies: C. × iyo Iyokan (伊予柑 - C. × iyo), juga dikenal sebagai anadomikan (穴門みかん) dan Gokaku no Iyokan,[1] adalah sebuah buah sitrus Jepang, yang penampilannya mirip dengan jeruk mandarin. Buah tersebut adalah buah sitrus paling banyak diproduksi kedua di Jepang setelah satsuma mandarin....
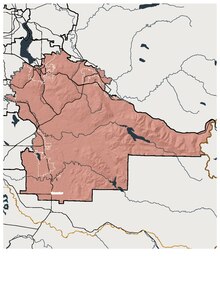
American legislative district Washington 5th legislative district map Washington's 5th legislative district is one of forty-nine districts in Washington state for representation in the state legislature. The district borders Kittitas County on the east, the 31st legislative district on the south, parts of Maple Valley, Renton, and Issaquah on the west, and Snohomish County on the north.[1] The largely rural district is represented by state senator Mark Mullet and state representatives...
European balance of power in the 19th century This article is about the 19th-century diplomatic term. For the jazz album, see European Concert. Concert of Europe1815 to 1848/1860s – 1871 to 1914The national boundaries within Europe as set by the Congress of Vienna, 1815Including Regency era Bourbon Restoration Revolutions of 1830 Revolutions of 1848 Causes of World War I Chronology Napoleonic era League of Nations The Concert of Europe was a general agreement among the great powers...

Nathanael Liminski (2023) Nathanael Liminski (* 19. September 1985 in Bonn) ist ein deutscher Politiker (CDU) in Nordrhein-Westfalen. Seit dem 29. Juni 2022 ist er Minister für Bundes- und Europaangelegenheiten, Internationales sowie Medien des Landes Nordrhein-Westfalen im Kabinett Wüst II und bereits seit dem 30. Juni 2017 Chef der Staatskanzlei des Landes Nordrhein-Westfalen (CdS). Liminski wurde als enger Vertrauter, langjähriger Mitarbeiter und Vordenker des gescheiterten CDU-Kan...

Decorative pattern of stylized foliage, characteristic of Muslim art For other uses, see Arabesque (disambiguation). Stone relief with arabesques of tendrils, palmettes and half-palmettes in the Umayyad Mosque, Damascus, Syria Part of a 15th-century ceramic panel from Samarkand (Uzbekistan) with white calligraphy on a blue arabesque backgroundThe arabesque is a form of artistic decoration consisting of surface decorations based on rhythmic linear patterns of scrolling and interlacing foliage,...

List of events ← 1784 1783 1782 1785 in the United States → 1786 1787 1788 Decades: 1770s 1780s 1790s 1800s See also: History of the United States (1776–1789) Timeline of the American Revolution List of years in the United States 1785 in the United States1785 in U.S. states States Connecticut Delaware Georgia Maryland Massachusetts New Hampshire New Jersey New York North Carolina Pennsylvania Rhode Island South Carolina Virginia List of years in the United States by state or ter...

Members of the New South Wales Legislative Council who served in the 58th Parliament were elected at the 2019 and 2023 elections. As members serve eight-year terms, half of the Council was elected in 2019 and did not face re-election in 2023, and the members elected in 2023 will not face re-election until 2031.[1][2] The President was Matthew Mason-Cox until May 2023[3] and Ben Franklin from May 2023. Name Party End term Years in office Mark Banasiak Shooters, ...























![{\displaystyle i\hbar {\frac {d\psi }{dt}}=\left[c\sum _{i=1}^{3}\alpha _{i}p_{i}+\alpha _{0}mc^{2}\right]\psi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/735fc4b857b229c30073896de01685ed6a1dcf38)

















![{\displaystyle \left[i\hbar c\left(\alpha _{0}{\frac {\partial }{c\partial t}}+\sum _{j=1}^{3}\alpha _{0}\alpha _{j}{\frac {\partial }{\partial x_{j}}}\right)-mc^{2}\right]\psi =0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5c25448000ca5910ad5e828acbf9931465d513f)














![{\displaystyle \sigma ^{\mu \nu }={\frac {i}{2}}\left[\gamma ^{\mu },\gamma ^{\nu }\right]_{-}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d76aaf33b2ff2e23aedb8a593053b0da67971b9f)
