Перетин прямих
|
Read other articles:

Grand Prix AustraliaSirkuit Grand Prix MelbourneInformasi lombaJumlah gelaran85Pertama digelar1928Terbanyak menang (pembalap) Lex Davison (4) Michael Schumacher (4)Terbanyak menang (konstruktor) Ferrari (13)Panjang sirkuit5.303 km (3.295 mi)Jarak tempuh307.574 km (191.071 mi)Lap58Balapan terakhir (2023)Pole position Max VerstappenRed Bull Racing-Honda RBPT1:16.732Podium 1. M. VerstappenRed Bull Racing-Honda RBPT2:32:38.371 2. L. HamiltonMercedes+0.179 3. F. AlonsoAston Ma...

Claudio BigagliClaudio Bigagli in Tu mi turbi, 1983Lahir8 Desember 1955 (umur 68)Montale, Tuscany, ItaliaPekerjaanPemeranTahun aktif1976-kini Claudio Bigagli (lahir 8 Desember 1955) adalah seorang pemeran asal Italia. Ia tampil dalam lebih dari 40 film dan acara televisi sejak 1976. Ia tampil dalam Fiorile, yang masuk dalam Festival Film Cannes 1993.[1] Filmografi pilihan The Face with Two Left Feet (1979) The Night of the Shooting Stars (1982) Via degli specchi (1982) Tu m...

A Series of Unfortunate Events PengarangLemony Snicket (pseudonim digunakan oleh) Daniel HandlerIlustratorBrett HelquistPerancang sampulBrett HelquistNegaraAmerika SerikatBahasaBahasa InggrisGenreBuku anak, komedi hitam, gothik, fiksi absurdisPenerbitHarperCollinsTgl. terbit (bhs. Inggris)30 September 1999 – 13 Oktober 2006 Halaman ini berisi artikel tentang serial buku. Untuk film, lihat Lemony Snicket's A Series of Unfortunate Events. Untuk permainan video, lihat Lemon...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Juni 2012. Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Pe...
Disambiguazione – Se stai cercando altri significati, vedi Rio de Janeiro (disambigua). Rio de JaneirocomuneMunicípio do Rio de Janeiro Rio de Janeiro – Veduta LocalizzazioneStato Brasile Stato federato Rio de Janeiro MesoregioneRio de Janeiro MicroregioneRio de Janeiro AmministrazioneSindacoEduardo Paes (PSD) dal 1º gennaio 2021 Data di istituzione1º marzo 1565 TerritorioCoordinate22°54′25″S 43°11′17″W / 22.906944°S 43.188056°W-22.9069...

Wi-fi network provided by local government Computer network typesby scale Nanoscale Near-field (NFC) Body Personal (PAN) Near-me Local (LAN) Storage (SAN) Wireless (WLAN) Virtual (VLAN) Home (HAN) Building Campus (CAN) Backbone Metropolitan (MAN) Municipal wireless (MWN) Wide (WAN) Cloud Internet Interplanetary Internet vte LinkNYC was announced by New York City Mayor Bill de Blasio in 2014 and will eventually replace the city's network of payphones. A municipal wireless network is a citywide...

Women's outer garment, popular in 19th century A visite in silk trimmed with beaver fur, 1885 A visite is a specific type of woman's outer garment similar to a mantle or wrap. It was particularly popular in the late 19th century, being specifically designed to accommodate the then fashionable bustle.[1] The visite replaced the huge shawls that had previously been worn over large crinoline skirts, combining shawl and coat elements, and was even on occasion made using shawls that were v...

Strongest Chil WooPoster promosi untuk Strongest Chil WooGenreDrama sejarahLagaDitulis olehBaek Wun-cheolSutradaraPark Man-yeongPemeranEric MunKu Hye-sunYoo Ah-inLee EonKim ByulNegara asalKorea SelatanBahasa asliKoreaJmlh. episode20ProduksiDurasiSenin dan Selasa pukul 21:55Rilis asliJaringanKBS2Format gambar480i (SDTV)1080i (HDTV)Rilis17 Juni (2008-06-17) –19 Agustus 2008 (2008-08-19) Strongest Chil WooHangul최강칠우 Hanja最強七迂 Alih AksaraChoegang ChilwoMcCune–R...

Deschampsia flexuosa Avenella flexuosa Canche flexueuseClassification GRIN Règne Plantae Famille Poaceae Sous-famille Pooideae Tribu Poeae Sous-tribu Airinae Genre Avenella EspèceAvenella flexuosa(L.) Drejer, 1838[1] Synonymes Aira flexuosa L., 1753 (basionyme) Deschampsia flexuosa (L.) Trin., 1836 etc. Avenella flexuosa, en français Canche flexueuse, Canche des montagnes, Deschampsie flexueuse[2] ou Foin tortueux[3], est une espèce de plantes à fleurs de la famille des Poaceae et du gen...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

Questa voce sull'argomento centri abitati del Mississippi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Ocean Springscity(EN) Ocean Springs, Mississippi Ocean Springs – Veduta LocalizzazioneStato Stati Uniti Stato federato Mississippi ConteaJackson AmministrazioneSindacoConnie Moran TerritorioCoordinate30°24′34.99″N 88°47′49.99″W30°24′34.99″N, 88°47′49.99″W (Ocean Springs) Altitudine7[1] m s.l.m. S...

H.M.A. TihamiLahir15 Agustus 1951 (umur 72)Serang, Banten, IndonesiaPekerjaanDosenSuami/istriFauziah Sy. Anasi Prof. Dr. HMA. Tihami, MA adalah Rektor IAIN Sultan Maulana Hasanuddin Banten Periode 2004-2010 (lahir 15 Agustus 1951) dari pasangan KH M Sulaiman dan Hj Zainab. Pernikahannya dengan Fauziah Syarbini Anasi dikaruniai anak: Helmy Faizi Bahrul Ulumi, Ivo Fauziastuti Tihamayati, Via Tuhamah Fauziastuti dan Ovi Fauzia Tihamayati. Pendidikan Formal SDN Pontang II, Pontang (1965) Ma...

Portuguese footballer In this Portuguese name, the first or maternal family name is Silva and the second or paternal family name is Coentrão. Fábio Coentrão Coentrão with Real Madrid in 2012Personal informationFull name Fábio Alexandre da Silva Coentrão[1]Date of birth (1988-03-11) 11 March 1988 (age 36)[1]Place of birth Vila do Conde, Portugal[1]Height 1.78 m (5 ft 10 in)[1]Position(s) Left-back, wingerYouth career1999–2006 Rio ...

Complex of several Hindu temples in Punjab, Pakistan Katas Raj Templesکٹاس راج مندرकटासराजThe temples surround a pond regarded as sacred by HindusReligionAffiliationHinduismDistrictChakwal districtDeityShivaLocationLocationChoa SaidanshahStatePunjabCountryPakistan Shown within Punjab, PakistanShow map of Punjab, PakistanKatas Raj Temples (Pakistan)Show map of PakistanGeographic coordinates32°43′26.4″N 72°57′05.9″E / 32.724000°N 72.951639°E&...

Public research university in Amherst, Massachusetts, US Not to be confused with Amherst College. University of Massachusetts AmherstLatin: Universitas MassachusettensisFormer namesMassachusetts Agricultural College (1863–1931)[1]Massachusetts State College (1931–1947)MottoEnse petit placidam sub libertate quietem (Latin)Motto in EnglishBy the sword we seek peace, but peace only under liberty.TypePublic land-grant research universityEstablishedApril 29, 1863; 161...

This article is part of a series onTaxation in the United States Federal taxation Alternative minimum tax Capital gains tax Corporate tax Estate tax Excise tax Gift tax Generation-skipping transfer tax Income tax Payroll tax Internal Revenue Service (IRS) Internal Revenue Code (IRC) IRS tax forms Revenue by state History Constitutional authority Taxpayer standing Court Protest Evasion Resistance State and local taxation State income tax Property tax Sales tax State and local tax deduction Us...

On the existence of a tangent to an arc parallel to the line through its endpoints For the theorem in harmonic function theory, see Harmonic function § The mean value property. For any function that is continuous on [ a , b ] {\displaystyle [a,b]} and differentiable on ( a , b ) {\displaystyle (a,b)} there exists some c {\displaystyle c} in the interval ( a , b ) {\displaystyle (a,b)} such that the secant joining the endpoints of the interval [ a , b ] {\displaystyle [a,b]} is parallel ...
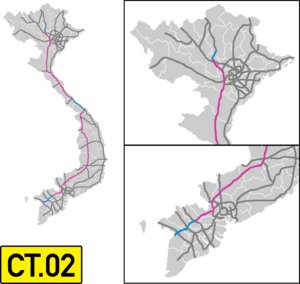
Bài viết hoặc đề mục này có chứa thông tin về một công trình hiện đang trong quá trình thi công.Nó có thể chứa thông tin có tính chất dự đoán, và nội dung có thể thay đổi lớn và thường xuyên khi quá trình xây dựng tiếp diễn và xuất hiện thông tin mới. Đừng nhầm lẫn với Đường cao tốc Bắc – Nam phía Đông. Đường cao tốcBắc – Nam phía TâyBảng kí hiệu đường cao tốc Bắc – Nam ...

この記事には複数の問題があります。改善やノートページでの議論にご協力ください。 出典がまったく示されていないか不十分です。内容に関する文献や情報源が必要です。(2021年2月) 雑多な内容を羅列した節があります。(2021年2月) あまり重要でない事項が過剰に含まれているおそれがあり、整理が求められています。(2021年2月)出典検索?: 日本列島ズバリ...

古代道路の例。東山道武蔵路跡(東京都国分寺市) 日本の古代道路(にほんのこだいどうろ)は、古代日本の道路または道路網を指す。特に、中央政府・律令体制構築期の政府が、古墳時代、飛鳥時代、奈良時代、平安時代前期にかけて計画的に整備・建設した道路または道路網を指す。 令文・史料には、駅、駅路、駅馬、伝馬の名が見られ、駅の制度と伝馬の制度と...




































































![{\displaystyle d_{i}^{2}={{\left[\left|\left|p-{{a}_{i}}\right|\right|\right]}^{2}}-{{\left[{{\left(p-{{a}_{i}}\right)}^{T}}*{{n}_{i}}\right]}^{2}}={{\left(p-{{a}_{i}}\right)}^{T}}*\left(p-{{a}_{i}}\right)-{{\left[{{\left(p-{{a}_{i}}\right)}^{T}}*{{n}_{i}}\right]}^{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d45f08b39fb50806e32f53c6b2b3d488c2bb3663)


![{\displaystyle {\underset {i}{\mathop {\sum } }}\,d_{i}^{2}={\underset {i}{\mathop {\sum } }}\,\left[{{\left(p-{{a}_{i}}\right)}^{T}}*\left(p-{{a}_{i}}\right)-{{\left[{{\left(p-{{a}_{i}}\right)}^{T}}*{{n}_{i}}\right]}^{2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/826ea130f757e6f4759f41b3905f2452d1659ffb)
![{\displaystyle {\underset {i}{\mathop {\sum } }}\,\left[2*\left(p-{{a}_{i}}\right)-2*\right[{{\left(p-{{a}_{i}}\right)}^{T}}*{{n}_{i}}]*{{n}_{i}}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88dc9b6afb099b69ef1670dbe49409488e934e36)
![{\displaystyle {\underset {i}{\mathop {\sum } }}\,\left(p-{{a}_{i}}\right)={\underset {i}{\mathop {\sum } }}\,\left[{{n}_{i}}*{{n}_{i}}^{T}\right]*\left(p-{{a}_{i}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3dd33cbc551e150164ebfb8ec356b009e4239e8d)
![{\displaystyle [{\underset {i}{\mathop {\sum } }}\,\left[{{n}_{i}}*{{n}_{i}}^{T}-I\right]]*p={\underset {i}{\mathop {\sum } }}\,\left[{{n}_{i}}*{{n}_{i}}^{T}-I\right]*{{a}_{i}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/587075fa921c47f9804acd965982ce93f3124264)




