Методи розв'язання нелінійних рівнянь
|
Read other articles:

Comic book series Ultimate Fantastic FourCover to Ultimate Fantastic Four #39Art by Salvador LarrocaPublication informationPublisherMarvel ComicsScheduleMonthlyFormatOngoing seriesGenre Superhero Publication dateFebruary 2004 – February 2009No. of issues60Main character(s)Reed RichardsSusan StormJohnny StormBenjamin GrimmCreative teamCreated byBrian Michael BendisMark MillarAdam Kubert(based upon the original characters by Stan Lee and Jack Kirby)Written byBrian Michael Bendi...

Trajectory of Earth around the Sun Not to be confused with Geocentric orbit. Earth at seasonal points in its orbit (not to scale) Earth orbit (yellow) compared to a circle (gray) Earth orbits the Sun at an average distance of 149.60 million km (8.317 light minutes, 92.96 million mi)[1] in a counterclockwise direction as viewed from above the Northern Hemisphere. One complete orbit takes 365.256 days (1 sidereal year), during which time Earth has traveled 940 million km (584 ...

Peta letak Pulau Talango Aeng Talango Aeng adalah sebuah pulau kecil di antara gugusan pulau-pulau di sebelah timur Pulau Madura. Secara administratif, pulau ini termasuk wilayah Kecamatan Raas), Kabupaten Sumenep, Jawa Timur. Raas sendiri merupakan nama sebuah pulau yang berada di sebelah barat daya Pulau Talango Aeng. lbsPulau di Jawa TimurKabupaten Banyuwangi Pulau Merah Kabupaten Gresik Pulau Bawean Kabupaten Jember Nusa Barung Kabupaten Malang Pulau Sempu Kabupaten Sampang Pulau Kambing ...
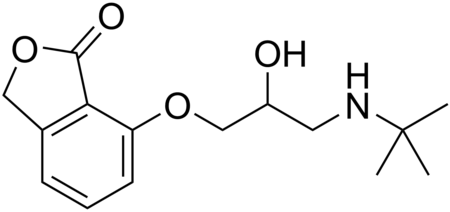
Chemical compound AfurololClinical dataATC codenoneIdentifiers IUPAC name 7-[3-(tert-Butylamino)-2-hydroxy-propoxy]-3H-isobenzofuran-1-one CAS Number65776-67-2 NPubChem CID176877ChemSpider154050 YUNIIWQ1WRV49R9ChEMBLChEMBL1742435 NChemical and physical dataFormulaC15H21NO4Molar mass279.336 g·mol−13D model (JSmol)Interactive image SMILES O=C1OCc2cccc(OCC(O)CNC(C)(C)C)c12 InChI InChI=1S/C15H21NO4/c1-15(2,3)16-7-11(17)9-19-12-6-4-5-10-8-20-14(18)13(10)12/h4-6,11,16-17H,7-9...

جزء من سلسلة مقالات سياسة الاتحاد الأوروبيالاتحاد الأوروبي الدول الأعضاء (27) إسبانيا إستونيا إيطاليا ألمانيا أيرلندا البرتغال بلجيكا بلغاريا بولندا جمهورية التشيك الدنمارك رومانيا سلوفاكيا سلوفينيا السويد فرنسا فنلندا قبرص كرواتيا لاتفيا لوكسمبورغ ليتوانيا مالطا المج...

Former trade union of the United States Metal and Machinery Workers Industrial UnionMerged intoMechanics Educational Society of AmericaFounded1907Dissolved1950LocationUnited States of AmericaKey peopleFrank CedervallAffiliationsIndustrial Workers of the World, Congress of Industrial OrganizationsWebsiteLink The Metal and Machinery Workers Industrial Union No. 440 (MMWIU) was a labor union in the United States which existed from 1907 to 1950. It organized workers in the manufacturing indu...

Pour les articles homonymes, voir Sainte-Colombe. Cet article est une ébauche concernant une commune de la Côte-d'Or. Vous pouvez partager vos connaissances en l’améliorant (comment ?). Le bandeau {{ébauche}} peut être enlevé et l’article évalué comme étant au stade « Bon début » quand il comporte assez de renseignements encyclopédiques concernant la commune. Si vous avez un doute, l’atelier de lecture du projet Communes de France est à votre disposition po...

Pour les articles homonymes, voir Première République. République françaisePremière République 21 septembre 1792 – 18 mai 1804(11 ans, 7 mois et 27 jours)Pavillon national de février 1794, en usage sur mer seulement Blason de la République Devise Liberté, Égalité, Fraternité Hymne La Marseillaise La République française (vert foncé) et ses républiques sœurs (vert clair), en 1799.Informations générales Statut État non reconnu Régime d'assemblée...

2013 single by YG featuring Jeezy and Rich Homie Quan My NiggaSingle by YG featuring Jeezy and Rich Homie Quanfrom the album My Krazy Life and Boss Yo Life Up Gang ReleasedSeptember 17, 2013 (2013-09-17)Recorded2013, The Blue Room Studios (Atlanta, Georgia)GenreHip hopLength3:56Label Pu$haz Ink CTE Def Jam Songwriter(s) Keenon Jackson Dijon McFarlane Mikely Adam Daniel Wall Jay Jenkins Dequantes Lamar Calvin Broadus Awood Johnson Craig Lawson Corey Miller Producer(s) DJ Mustard...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: New England town – news · newspapers · books · scholar · JSTOR (May 2023) (Learn how and when to remove this message) Unit of government in New England, US TownAlso known as:New England town This map shows the six New England states and their local political su...

Monts du Forez Carte de localisation des monts du Forez. Géographie Altitude 1 631 m, Pierre-sur-Haute Massif Massif central Administration Pays France Région Auvergne-Rhône-Alpes Départements Haute-Loire, Puy-de-Dôme, Loire Géologie Âge Paléozoïque Roches Granite modifier Les monts du Forez sont une chaîne de montagne du Massif central séparant la vallée de la Dore de la plaine du Forez. Ils culminent à Pierre-sur-Haute à 1 631 mètres d'altitude. Top...

Sceaux 行政国 フランス地域圏 (Région) イル=ド=フランス地域圏県 (département) オー=ド=セーヌ県郡 (arrondissement) アントニー郡小郡 (canton) 小郡庁所在地INSEEコード 92071郵便番号 92330市長(任期) フィリップ・ローラン(2008年-2014年)自治体間連合 (fr) メトロポール・デュ・グラン・パリ人口動態人口 19,679人(2007年)人口密度 5466人/km2住民の呼称 Scéens地理座標 北緯48度4...

Fictional planets and moons in the Star Wars media franchise Star Wars galaxy redirects here. For the video game, see Star Wars Galaxies. For the comic series named Star Wars Galaxy, see Star Wars (UK comics). Nevarro redirects here. Not to be confused with Navarro. Carida redirects here. For the synonym of a genus of shrimp, see Hippolyte (crustacean). Remains of the film set for the Lars Homestead on the Planet Tatooine at Chott el-Jerid, Tunisia (pictured in 2010) The fictional universe of...

GarcimoreGarcimore au Festival de l'Ille de Betton en 1977.BiographieNaissance 16 novembre 1940Elche de la Sierra (province d'Albacete, Espagne)Décès 18 avril 2000 (à 59 ans)Le Gué-de-Longroi (Eure-et-Loir, France)Sépulture Le Gué-de-LongroiNom de naissance José García MorenoNationalités espagnolefrançaiseActivité PrestidigitateurPériode d'activité 1962-2000Autres informationsA travaillé pour TF1Radiodiffusion-télévision françaisemodifier - modifier le code - modifier Wi...

This is a list megalopolises grouped by geographical region and country. Africa Nile Delta and Nile River at night from space Pretoria, South Africa Nairobi, Kenya Lagos, Nigeria Country Megalopolis Major cities and areas Populationestimate Egypt Greater Cairo The Governorates of Cairo, Giza, Qalyubiyya and Helwan 22,183,000[1] Nile Delta Governorates of Alexandria, Beheira, Kafr el-Sheikh, Gharbia, Monufia, Qalyubiyya, Dakahlia, Damietta, Al Sharqia, and Port Said 50,322,424&#...

Prisoner at Guantanamo Bay detention camp Ammar al-BaluchiBaluchi's detainee assessment memorandum by the U.S. Department of Defense, 8 December 2006BornAli Abdul Aziz Ali (1977-08-29) 29 August 1977 (age 46)[1]Al Ahmadi, KuwaitArrested29 April 2003Karachi, PakistanCitizenshipPakistaniDetained at Guantánamo Bay, CubaISN10018OccupationComputer technicianSpouse Aafia Siddiqui (m. 2003; div. 2003)RelativesKhalid Sheikh Mohamm...

1874 tone poem written by Camille Saint-Saëns For the medieval allegory, see Danse Macabre. Danse macabre, Op. 40, is a symphonic poem for orchestra, written in 1874 by the French composer Camille Saint-Saëns. It premiered 24 January 1875. It is in the key of G minor. It started out in 1872 as an art song for voice and piano with a French text by the poet Henri Cazalis, based on the play Danza macàbra by Camillo Antona-Traversi.[1] In 1874, the composer expanded and reworked the pi...

Questa voce sull'argomento giornalisti italiani è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Gazzaniga in visita alla squadra di calcio dell'Empoli nella seconda metà degli anni 80, mentre posa tra l'allenatore Salvemini (a sinistra) e l'attaccante Ekström (a destra) Gian Maria Gazzaniga (Codevilla, 6 giugno 1927 – Retorbido, 11 agosto 2009) è stato un giornalista italiano[1]. Biografia...

2010 Mauritian general election ← 2005 5 May 2010 2014 → All 70 seats in the National Assembly35 seats needed for a majority First party Second party Leader Navin Ramgoolam Paul Berenger Party Labour Party MMM Alliance PTR–PMSD–MSM MMM–UN–MMSD Seats won 41 19 Popular vote 1,001,903 847,095 Percentage 49.69% 42.01% Prime Minister before election Navin Ramgoolam Labour Party Subsequent Prime Minister Navin Ramgoolam Labour Party Politics of...

Subdivision of the Soviet occupation zone and one of the states of Soviet East Germany State of BrandenburgLand Mark Brandenburg (1947) Provinz Mark Brandenburg (1945–1947) Subdivision of the Soviet occupation zone State of East Germany 1947–1952 Flag Coat of arms Brandenburg within Allied-occupied Germany in 1947Comparison of the country borders of 1947 (violet) and 1990 (red); since 1990 the State of Berlin covers the Greater Berlin area.CapitalPotsdamArea • 195027,612 ...


![{\displaystyle [x_{1},x_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91bdff343d848c2b70c68b5c04a2479b14a9fef0)









