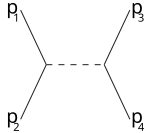
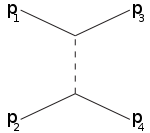
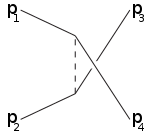
Кінематичні змінні Мандельштама
|
Read other articles:

Barony in the Peerage of the United Kingdom This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Baron Brabazon of Tara – news · newspapers · books · scholar · JSTOR (April 2020) Baron Brabazon of Tara, of Sandwich in the County of Kent, is a title in the Peerage of the United Kingdom. It was created on...

أُنشئت أسس النظام الصحي الموحد في الدستور البرازيلي لعام 1988، بموجب مبادئ العالمية والتكامل والإنصاف. البرازيل لديها نظام تشغيل وإدارة لامركزي، والمشاركة الاجتماعية موجودة على جميع المستويات الإدارية.[1] النظام الصحي البرازيلي هو تركيبة معقدة يتشارك فيها القطاع العا�...

Fictional robot from Borderlands Fictional character ClaptrapBorderlands characterFirst appearanceBorderlands (2009)Created byGearbox SoftwareVoiced by Various David Eddings (Borderlands, Borderlands 2, Borderlands: The Pre-Sequel, Tales from the Borderlands) Jim Foronda (Borderlands 2 VR, Commander Lilith & the Fight for Sanctuary DLC, Borderlands 3, Tiny Tina's Wonderlands) Jack Black (film) In-universe informationSpeciesModel CL4P-TP Steward Bot Claptrap is a fictional character that a...

Cet article est une ébauche concernant l’économie. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Pour l’article homonyme, voir Intensité énergétique (physique). L’intensité énergétique est une mesure de l'efficacité énergétique d'une économie. Elle est calculée comme le quotient de la consommation d'énergie au produit intérieur brut. Elle est généralement exprimée en tonnes équivalent ...

Cet article est une ébauche concernant les monuments historiques français et l’Ille-et-Vilaine. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Fours à chauxFours à Chaux à Chartres-de-Bretagne.PrésentationType Four à chauxFondation 1865, 1876Patrimonialité Inscrit MH (1987)LocalisationCommune Chartres-de-BretagneCoordonnées 48° 02′ 37″ N, 1° 43′ 00″ OLocal...

Papa Innocenzo VIII213º papa della Chiesa cattolica Elezione29 agosto 1484 Incoronazione12 settembre 1484 Fine pontificato25 luglio 1492(7 anni e 331 giorni) Cardinali creativedi Concistori di papa Innocenzo VIII Predecessorepapa Sisto IV Successorepapa Alessandro VI NomeGiovanni Battista Cybo de Mari NascitaGenova, 1432 Ordinazione sacerdotalein data sconosciuta Nomina a vescovo5 novembre 1466 da papa Paolo II Consacrazione a vescovo28 gennaio 1467 Creazione a cardinale7 mag...

Sculpture by Auguste Rodin GlaucusBronze version, Museo Soumaya, Mexico CityArtistAuguste RodinYear1889MediumPlaster, later bronze Glaucus is a sculpture by the French artist Auguste Rodin, first conceived in 1886 as a representation of the mythological figure Glaucus, son of Poseidon. Originally made in plaster, bronze casts of it are now in the Brooklyn Museum and the Museo Soumaya. Inspiration It was one of many studies arising from Rodin's reading of Ovid's Metamorphoses, here drawing on ...

Об одноимённом фильме см. Наркотик (фильм). Аптечная упаковка героина, XIX век Марихуана, или каннабис (содержит Тетрагидроканнабинол) Нарко́тик (от греч. ναρκωτικός — приводящий в оцепенение, греч. νάρκωσις — ступор) — согласно определению ВОЗ, «химический а�...

此條目需要补充更多来源。 (2021年7月4日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:美国众议院 — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 美國眾議院 United States House of Representatives第118届美国国会众议院徽章 众议院旗...

Red Bull RB16B Max Verstappen (ici lors du GP d'Autriche qu'il remporte) champion du monde 2021 au volant de la RB16B. Présentation Équipe Red Bull Racing Honda Constructeur Red Bull Racing Année du modèle 2021 Concepteurs Adrian NeweyPierre Waché Rob Marshall Dan Fallows Spécifications techniques Châssis Monocoque composite moulée en fibre de carbone et nid d'abeilles Suspension avant Doubles triangles superposés, poussoirs, basculeurs avec barre de torsion et barres anti-roulis Su...

Empire on the Indian subcontinent, 1799–1849 Not to be confused with Kingdom of Sikkim. Sikh EmpireSarkār-i-KhālsaKhālasā Rāj1799–1849 Flag Seal of Ranjit Singh Motto: ਅਕਾਲ ਸਹਾਇAkāl SahāiWith God's GraceAnthem: ਦੇਗ ਤੇਗ ਫ਼ਤਿਹDēg Tēg FatehVictory to Charity and ArmsSikh Empire at the death of Ranjit Singh in 1839StatusEmpireCapital Gujranwala (1799–1802) Lahore (1802–1849) Court languagePersian[1][2][3]Spo...

2nd-century Christian apocalyptic text For the Nag Hammadi text, see Gnostic Apocalypse of Peter. For the 10th-century Arabic text, see Arabic Apocalypse of Peter. The beginning of the Greek fragment of the Apocalypse of Peter found in Akhmim, Egypt Part of a series onNew Testament apocryphaFirst page of the Gospel of Judas(Page 33 of Codex Tchacos) Apostolic Fathers 1 Clement 2 Clement Epistles of Ignatius Polycarp to the Philippians Martyrdom of Polycarp Didache Barnabas Diognetus The Sheph...

Diane NguyenTokoh BoJack HorsemanPenampilanperdanaBoJack Horseman: The BoJack Horseman Story, Chapter One (2014)PenciptaRaphael Bob-WaksbergPengisi suaraAlison BrieInformasiNama lengkapDiane NguyenSpesiesManusiaPekerjaanPenulisKeluarga Ma Nguyen (ibu) Pa Nguyen (ayah; almarhum) Marty, Artie, Gary, dan Tommy Nguyen (saudara) Pihak lain Mr. Peanutbutter (mantan suami) Guy (suami) Diane Nguyen (kelahiran 19 Maret 1980) adalah sebuah karakter fiksi dari seri televisi animasi Netflix BoJack Horsem...

La Renaissance (Prancis)E Zingo (Sango)Lagu kebangsaan Republik Afrika TengahPenulis lirikBarthélémy BogandaKomponisHerbert PepperPenggunaan1960 La Renaissance (Terlahir kembali) adalah lagu kebangsaan Republik Afrika Tengah. Lirik lagu ini diciptakan oleh Barthélémy Boganda. Adapun komposisi lagu ini disusun oleh Herbert Pepper. Lirik Ô Centrafrique, ô berceau des Bantous ! Reprends ton droit au respect, à la vie ! Longtemps soumis, longtemps brimé par tous, Mais de c...

You can help expand this article with text translated from the corresponding article in Hungarian. (November 2019) Click [show] for important translation instructions. View a machine-translated version of the Hungarian article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English...

2008 film by Andrew Stanton This article is about the animated film. For the title character, see WALL-E (character). For other uses, see WALL-E (disambiguation) and Walle. WALL•ETheatrical release posterDirected byAndrew StantonScreenplay by Andrew Stanton Jim Reardon Story by Andrew Stanton Pete Docter Produced byJim MorrisStarring Ben Burtt Elissa Knight Jeff Garlin Fred Willard John Ratzenberger Kathy Najimy Sigourney Weaver Cinematography Jeremy Lasky Danielle Feinberg Edited byStephen...

Fat-soluble vitamers This article is about the family of vitamers. For vitamin K1, the form most commonly used as a dietary supplement or in a multi-vitamin, see Phytomenadione. Vitamin KDrug classVitamin K structures.Class identifiersUseVitamin K deficiency, Warfarin overdoseATC codeB02BABiological targetGamma-glutamyl carboxylaseClinical dataDrugs.comMedical EncyclopediaExternal linksMeSHD014812Legal statusIn Wikidata Vitamin K is a family of structurally similar, fat-soluble vitamers found...

Cells that primarily compose adipose tissue, specialized in storing energy as fat AdipocyteIllustration depicting white fat cells.Morphology of three different classes of adipocytesDetailsIdentifiersLatinadipocytusMeSHD017667THH2.00.03.0.01005 FMA63880Anatomical terms of microanatomy[edit on Wikidata] Adipocytes, also known as lipocytes and fat cells, are the cells that primarily compose adipose tissue, specialized in storing energy as fat.[1] Adipocytes are derived from mesenchym...

Region in Tanzania Region in Lake, TanzaniaSingida Region Mkoa wa Singida (Swahili)Region From top to bottom: Lake Singidani, Misuni Rocks in Misuni ward, Singida & High rise in Utemeni ward, Singida MunicipalNickname: Tanzania's heartlandLocation in TanzaniaCoordinates: 6°44′43.08″S 34°9′11.52″E / 6.7453000°S 34.1532000°E / -6.7453000; 34.1532000Country TanzaniaZoneLakeRegion15 October 1963CapitalSingidaDistricts List Ikungi DistrictItig...

Historic church in Massachusetts, United States United States historic placeTrinity Episcopal ChurchU.S. National Register of Historic Places Show map of MassachusettsShow map of the United StatesLocationMelrose, MassachusettsCoordinates42°27′34″N 71°04′07″W / 42.45937°N 71.06865°W / 42.45937; -71.06865Built1886ArchitectCharles Brigham; Smith, WilliamArchitectural styleLate 19th And 20th Century Revivals, Shingle StyleNRHP reference No.950006...