Коефіцієнт кластеризації
|
Read other articles:

Untuk film yang berjudul sama, lihat Thumbelina (film 1994). ThumbelinaIlustrasi karya Vilhelm Pedersen,Ilustrator pertama AndersenPengarangHans Christian AndersenJudul asliTommelisePenerjemahMary HowittNegaraDenmarkBahasaDenmarkGenreCerita dongeng sastraTerbitanFairy Tales Told for Children. First Collection. Buklet Kedua. 1835. (Eventyr, fortalte for Børn. Første Samling. Andet Hefte. 1835.)Jenis terbitanKumpulan cerita dongengPenerbitC. A. ReitzelJenis mediaCetakTanggal terbit16 Desember...

Dutch art historian Rookmaaker with students, 1970 Henderik Roelof Hans Rookmaaker (February 27, 1922 – March 13, 1977) was a Dutch Christian scholar, professor, and author who wrote and lectured on art theory, art history, music, philosophy, and religion. In 1948 he met Christian theologian Francis Schaeffer and became a member of L'Abri in Switzerland. Rookmaaker and his wife Anky opened a Dutch branch of L'Abri in 1971. Following a doctorate in art history with a dissertation on Gauguin ...

Branch of the Teutonic Order, 1237–1561 Not to be confused with Livonian Brothers of the Sword. Livonian Order Seal of the Livonian Order's masterVTOIINLIVONIA MENDATORIS•DOMand the coat of arms of Teutonic Knights in the Livonian Order [citation needed]Active1237–1561Country State of the Teutonic Order (1237–1435) Livonian Confederation (1435–1561) BranchTeutonic OrderGarrison/HQWenden (Cēsis), Fellin (Viljandi)Battle honoursLivonian Crusade, Battle of the Ice, Wesenb...

Pour les articles homonymes, voir Réforme. Ne doit pas être confondu avec Calendrier grégorien. Grégoire VII, miniature du XIIe siècle. La réforme grégorienne est une politique menée durant le Moyen Âge sous l'impulsion de la papauté. Si les historiens admettent que le pape Léon IX (1049-1054) a commencé le redressement de l'Église, c'est néanmoins le pape Grégoire VII (1073-1085) qui a laissé son nom à la réforme. De plus, les efforts pour sortir l'Égl...

Andi Herry IskandarAndi Herry Iskandar sebagai Wakil Wali Kota Makassar (2004–2009) Penjabat Bupati MarosMasa jabatan27 Agustus 2015 – 17 Februari 2016PresidenJoko WidodoGubernurSyahrul Yasin Limpo PendahuluM. Hatta RahmanPenggantiM. Hatta RahmanPenjabat Bupati Luwu UtaraMasa jabatan28 Agustus 2010 – 3 November 2010PresidenSusilo Bambang YudhoyonoGubernurSyahrul Yasin Limpo PendahuluArifin JunaidiPenggantiArifin JunaidiWali Kota Makassar Ke-19Masa jabatan2008–200...

New York City Subway service New York City Subway serviceBroadway ExpressAn Astoria–Ditmars Boulevard-bound N train of R46s leaving 30th AvenueNote: Dashed red line shows late night service via the Montague Street Tunnel. Dashed pink line shows limited rush hour service to/from 96th Street.Northern end Astoria–Ditmars Boulevard (all times) 96th Street–Second Avenue (limited rush hour service) Southern endConey Island–Stillwell AvenueStations28 (weekdays)32 (weekends)45 (late...

هذه المقالة عن قافزات الأوراق. لمعانٍ أخرى، طالع قافز (توضيح). تحتاج النصوص المترجمة في هذه المقالة إلى مراجعة لضمان معلوماتها وإسنادها وأسلوبها ومصطلحاتها ووضوحها للقارئ، لأنها تشمل ترجمة اقتراضية أو غير سليمة. فضلاً ساهم في تطوير هذه المقالة بمراجعة النصوص وإعادة...

Bupati KupangPetahanaAlexon Lumba, M.Hum. (Pj.)sejak 7 April 2024Masa jabatan5 tahunDibentuk1958Pejabat pertamaC.M.K. Amalo (ad interim);Willem Cornelis Hendrik Oematan (definitif)Situs webkupangkab.go.id Berikut merupakan Daftar Bupati Kupang dari masa ke masa. No. Potret Nama Bupati (Masa Hidup) Mulai Menjabat Selesai Menjabat Prd. Jabatan Sebelumnya Wakil Bupati Ref. sebelum DPRD Kab. Kupang terbentuk dan melakukan pemilihan bupati, C.M.K. Amalo menjabat sebagai Pejabat Bupati Kupang ...

Two regions of Ancient Egypt In Egyptian history, the Upper and Lower Egypt period (also known as The Two Lands) was the final stage of prehistoric Egypt and directly preceded the unification of the realm. The conception of Egypt as the Two Lands was an example of the dualism in ancient Egyptian culture and frequently appeared in texts and imagery, including in the titles of Egyptian pharaohs. The Egyptian title zmꜣ-tꜣwj (Egyptological pronunciation sema-tawy) is usually translated as Uni...

Political convention 1976 Democratic National Convention1976 presidential election NomineesCarter and MondaleConventionDate(s)July 12–15, 1976CityNew York CityVenueMadison Square GardenKeynote speakerBarbara JordanCandidatesPresidential nomineeJimmy Carter of GeorgiaVice presidential nomineeWalter Mondale of Minnesota‹ 1972 · 1980 › Madison Square Garden was the site of the 1976 Democratic National Convention Barbara Jordan delivering the keynote address on the firs...

Line of tower computers designed and manufactured by Apple Not to be confused with iMac G5, Power Mac G4, iMac G4, Power Mac G4 Cube, PowerBook G4, or iBook G4. Power Mac G5Apple Power Mac G5DeveloperApple Computer, Inc.Product familyPower MacintoshTypeDesktopRelease dateJune 23, 2003Introductory priceUS$1,999 (equivalent to $3,310 in 2023)DiscontinuedAugust 7, 2006CPU1.6 – 2.7 GHz PowerPC G5Single-processorDual-processors, single-coreDual-coreDual-processors, dual-corePredecessorPower ...

For the Japanese pottery, see Shikokai. Political party in Japan Shikōkai 志公会LeaderTarō AsōFounderTarō AsōFounded3 July 2017Preceded byBanchō Seisaku KenkyūjoIdeologyConservatismBig tentTypeLiberal Democratic Party factionCouncillors15 / 117Representatives41 / 259Politics of JapanPolitical partiesElections Shikōkai (Japanese: 志公会) is a faction led by Tarō Asō[1] within the Liberal Democratic Party (LDP).[2] It is currently the third-largest facti...

В Википедии есть статьи о других людях с фамилией Лукьянова. Кира Александровна Лукьянова Дата рождения 23 ноября 1962(1962-11-23) (61 год) Место рождения Саратов, РСФСР, СССР Гражданство Россия Род деятельности предпринимательница, политик, депутатка Государственной дум�...

Universidad Internacional de KirguistánМеждународный университет Кыргызстана Tipo PúblicaFundación 1993LocalizaciónDirección Biskek, KirguistánCoordenadas 42°52′39″N 74°35′08″E / 42.877451, 74.585494Sitio web http://iuk.kg/[editar datos en Wikidata] La Universidad Internacional de Kirguistán[1][2] (en ruso: Международный университет Кыргызстана) es una universid...

Nemzeti Bajnokság I 1909-1910 Competizione Nemzeti Bajnokság I Sport Calcio Edizione 9ª Organizzatore MLSZ Luogo Ungheria Partecipanti 9 Risultati Vincitore Ferencváros(5º titolo) Retrocessioni MAC Statistiche Miglior marcatore Imre Schlosser (19) Cronologia della competizione 1908-1909 1910-1911 Manuale L'edizione 1909-10 del Nemzeti Bajnokság I vide la vittoria finale del Ferencvárosi TC, che conquista il suo quinto titolo, il secondo consecutivo. Capocannoniere...

莎拉·阿什頓-西里洛2023年8月,阿什頓-西里洛穿著軍服出生 (1977-07-09) 1977年7月9日(46歲) 美國佛羅里達州国籍 美國别名莎拉·阿什頓(Sarah Ashton)莎拉·西里洛(Sarah Cirillo)金髮女郎(Blonde)职业記者、活動家、政治活動家和候選人、軍醫活跃时期2020年—雇主內華達州共和黨候選人(2020年)《Political.tips》(2020年—)《LGBTQ國度》(2022年3月—2022年10月)烏克蘭媒�...

نهر تاريم خريطة توضح أنهار حوض تاريم خريطة من الاٌقمار الصناعية لحوض تاريم المنطقة البلد آسيا ، الصين ، تركستان الصينية ، شينجيانغ الخصائص الطول 1,321 كـم (821 ميل)[1] المجرى المنبع الرئيسي جبال كونلون وقراقرم » الإحداثيات 39°28′N 88°19′E / 39.467°N 88.317°E / 39.467...
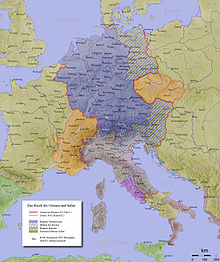
People of Germany This article is about the people of Germany. For other uses, see German. Ethnic group GermansGerman: DeutscheRegions with significant populationsGermany72,569,978[a]United States534,000[b] c. 42,600,000[3]Brazil21,000[c] c. 5,000,000[4][5]Canada157,000[d] c. 3,322,405[6]Australia125,000[e] 1,026,140[7]Kazakhstanc. 900,000[8]Russia142,000[f] c. 840,000[8]Argentina9,000[...

Piala Liga Inggris 1990–19911990–91 Football League CupNegara Inggris WalesTanggal penyelenggaraan27 Agustus 1990 s.d. 21 April 1991Jumlah peserta92Juara bertahanNottingham ForestJuaraSheffield Wednesday(gelar ke-1)Tempat keduaManchester UnitedPencetak gol terbanyakPaul GascoigneMark Hughes(6 gol)← 1989–1990 1991–1992 → Piala Liga Inggris 1990–1991 adalah edisi ke-31 penyelenggaraan Piala Liga Inggris, sebuah kompetisi dengan sistem gugur untuk 92 tim terbaik di Inggri...

Questa voce sugli argomenti attori francesi e registi francesi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Pascal Bonitzer Pascal Bonitzer (Parigi, 1º febbraio 1946) è un attore, sceneggiatore e regista francese. In veste di sceneggiatore, ha collaborato in più occasioni con Jacques Rivette ed André Téchiné. In veste di regista, con il suo film d'esordio Encore (1996) ha vinto il Premio Jean ...




























