Квадратури Гауса
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Bahasa diWalesResmi Wales[1] Inggris (de facto) Bahasa nasional Wales (29,3%),[2] Inggris Utama Wales atau Inggris 96,7% Polski 0,7% Arab 0,3%[3] AsingPrancis, Jerman, Spanyol atau Tionghoa[4]IsyaratBahasa Isyarat BritaniaTata letak papan tombolQWERTY L • B • PWBantuan penggunaan templat ini Bagian dari seri tentangBudaya Wales Bangsa Bahasa Bahasa Wales (Y Fro Gymraeg Sejarah Nama tempat Wales Nama keluarga Wales Pendidikan media Wales) Bahasa In...

Ini adalah nama Batak Toba, marganya adalah Pardosi. Freddy Jhon Hamonangan Pardosi Asrena Kaskogabwilhan III Informasi pribadiLahir14 Desember 1971 (umur 52)Balige, Sumatera UtaraSuami/istriNy. Christina Romauli C. Siboro, S.Sos.AnakVirgie Samantha P PardosiChelsea Maria N PardosiRalph Samuel H PardosiJonathan Matthew H PardosiAlma materAkademi Angkatan Laut (1994)Karier militerPihak IndonesiaDinas/cabang TNI Angkatan LautMasa dinas1994—sekarangPangkat Brigadir Jenderal TNI ...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: List of Filipino Catholic saints and beatified people – news · newspapers · books · scholar · JSTOR (June 2016) (Learn how and when to remove this template message) This is a list of Filipino saints, beati, venerables, and Servants of God by the Catholic Churc...

För andra betydelser, se Manilla (olika betydelser). Manila (Lungsod ng Maynila) Huvudstad Motto: Linisin Ikarangal ang Maynila (Cleanse, Take Pride of Manila) Smeknamn: Perla del Oriente (Pearl of the Orient); Queen of the Orient; The City of Our Affections; City by the Bay; La Insigne y Siempre Leal Ciudad (Distinguished and Ever Loyal City) Land Filippinerna Region Metro Manila Distrikt 1:a till 6:e distriktet Barangays 897 Höjdläge 16 m ö.h. Koordinater...

Zona di India Pembagian administratif India secara hierarkis terdiri atas (1) negara bagian dan wilayah persatuan, (2) distrik, (3) tehsil, serta (4) desa. Sejumlah 29 negara bagian dan 7 wilayah persatuan dikelompokkan ke dalam 5 zona besar. Negara bagian dan wilayah persatuan dibagi menjadi distrik yang berjumlah 640 di seluruh India. India terbagi atas 29 negara bagian, 6 Wilayah persatuan, dan sebuah Wilayah Ibu Kota Nasional. Andhra Pradesh Arunachal Pradesh Assam Bihar Chhattisgarh Ibu ...
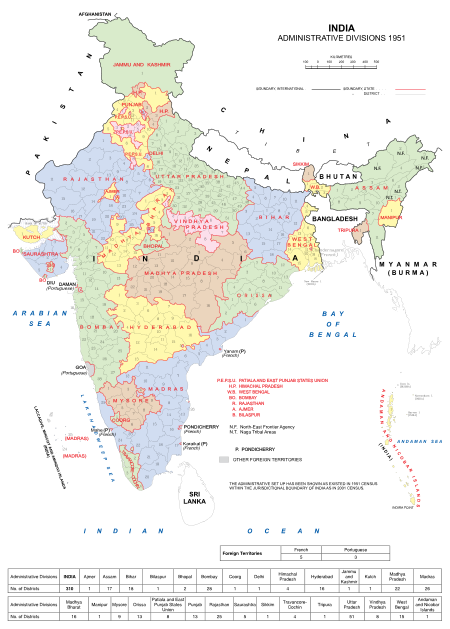
1952 Bombay Legislative Assembly election ← 1946 26 March 1952 1957 → All 315 seats in the Bombay Legislative Assembly158 seats needed for a majorityRegistered16,712,606Turnout50.78% Majority party Minority party Party INC PWPI Seats won 269 14 Popular vote 49.95% 6.45% CM before election B. G. Kher INC Elected CM Morarji Desai INC Indian administrative divisions, as of 1951 Elections to the Legislative Assembly of the Indian state of Bombay were...

Historic house in Virginia, United States United States historic placeEsmontU.S. National Register of Historic PlacesVirginia Landmarks Register Front of the estate houseShow map of VirginiaShow map of the United StatesLocationNorth of Esmont, near Esmont, VirginiaCoordinates37°50′33″N 78°36′23″W / 37.84250°N 78.60639°W / 37.84250; -78.60639Area53 acres (21 ha)Built1818 (1818)Built byFloyd JohnsonArchitectural styleEarly Republic, Jeffersonia...

يسرائيل كاتس (بالعبرية: ישראל כץ) معلومات شخصية الميلاد 21 سبتمبر 1955 (العمر 68 سنة)عسقلان الإقامة كفر أحيم [لغات أخرى][1] مواطنة إسرائيل عضو في لواء المظليين الإسرائيلي مناصب عضو الكنيست[1] عضو خلال الفترة18 نوفمبر 1998 – 23 فبراير 1999 فترة...

Nicolas de Plattemontagne; potret oleh Jean Ranc Nicolas de Plattemontagne, nama aslinya Nicolas Van Plattenberg[1] (19 November 1631, Paris - 25 Desember 1706[2]) adalah seorang pelukis dan pengukir Prancis. Namanya juga muncul sebagai La Montagne, Montagne dan Montaigne. Ayahandanya adalah pelukis dan pengukir flamand Matthieu van Plattenberg, berasal dari Antwerpen, yang mengkhususkan diri dalam adegan maritim. Selain itu, pamandanya adalah pengukir terkenal, Jean Morin, ya...

1987 United States Supreme Court caseSan Francisco Arts & Athletics, Inc. v. United States Olympic CommitteeSupreme Court of the United StatesArgued March 24, 1987Decided June 25, 1987Full case nameSan Francisco Arts & Athletics, Inc. v. United States Olympic CommitteeCitations483 U.S. 522 (more)107 S. Ct. 2971; 97 L. Ed. 2d 427; 1987 U.S. LEXIS 2895Case historyPriorSummary judgment for respondent granted, 219 U.S.P.Q. 982 (N.D. Cal., 1982); affirmed, 781 F.2d 733 (9th Cir. 1986), re...

1992 single by the Cranberries DreamsArtwork for 1994 European rerelease (UK CD1 single pictured)Single by the Cranberriesfrom the album Everybody Else Is Doing It, So Why Can't We? B-side What You Were Liar Released28 September 1992 (1992-09-28)[1]Genre Alternative rock dream pop[2][3] Length 4:32 (album version) 4:15 (UK radio edit) 4:02 (US radio edit) LabelIslandSongwriter(s)Dolores O'Riordan, Noel HoganProducer(s)Stephen StreetThe Cranberries single...

AntropologiVenus of Willendorf Bidang Antropologi biologis Antropologi budaya Antropologi linguistik Antropologi sosial Arkeologi Sub bidang Antropologi agama Antropologi ekologi Antropologi ekonomi Antropologi forensik Antropologi hukum Antropologi media Antropologi kedokteran Antropologi perkotaan Antropologi visual Etnologi Sosiologi Metode dan kerangka kerja Antropologi terapan Etnografi Observasi peserta Metode kualitatif Relativisme budaya Konsep utama Budaya · Masyarakat Praseja...

Questa voce sull'argomento stagioni delle società calcistiche italiane è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Voce principale: Vicenza Calcio. Associazione Del Calcio Di VicenzaStagione 1921-1922Sport calcio SquadraVicenza Calcio Allenatore Giulio Fasolo poi Aldo Casalini e Pio Scala Presidente Riccardo Sebellin Prima Divisione12º posto nel Girone A della Lega Nord di Prima Divisione (Retroc...

John Harrison= John HarrisonLahir3 April [K.J.: 24 Maret] 1693Foulby, dekat Wakefield, West Riding of Yorkshire, InggrisMeninggal24 Maret 1776(1776-03-24) (umur 82)London, InggrisTempat tinggalRed Lion SquareKebangsaanInggrisDikenal atasKronometer lautPenghargaanCopley Medal (1749)Karier ilmiahBidangHorologi John Harrison (3 April [K.J.: 24 Maret] 1693 – 24 Maret 1776) adalah seorang tukang kayu dan pembuat jam otodidak asal Inggris yang menciptakan kronometer laut, sebuah alat untuk ...

Building in Vermont, United States United States historic placeJedediah II Strong HouseU.S. National Register of Historic Places Show map of VermontShow map of the United StatesLocationQuechee Main St. and Dewey's Mills Rd., Hartford, VermontCoordinates43°38′44″N 72°24′2″W / 43.64556°N 72.40056°W / 43.64556; -72.40056Arealess than one acreBuilt1815 (1815)Built byStrong, Jedediah IIArchitectural styleFederalNRHP reference No.74000272[...

Французские Южные и Антарктические территории фр. Terres australes et antarctiques françaises (Флаг ФЮАТ) (Герб ФЮАТ) Местоположение Администрация Административный центр Сен-Пьер или Порт-о-Франсэ (неофиц.) Префект Паскаль Болот(фр. Pascal Bolot) Округа 5 Статистика Площадь1 439 672без Земли Аде...

У этого термина существуют и другие значения, см. Дананг (значения). Город центрального подчиненияДанангвьетн. Đà Nẵng 16°02′55″ с. ш. 108°13′14″ в. д.HGЯO Страна Вьетнам Внутреннее деление 6 городских районов, 1 сельский уезд, 1 островной архипелаг История и географи...

Gregory Sams at the Glade Festival in 2006.Gregory Sams (born 1948 in Los Angeles, California) is a UK-based, American-born, fractal artist, author and publisher. Life and works Greg has been a wheelchair user since falling from a tree whilst a freshman at the University of California, Berkeley.[1] Greg moved to London and, aged 19, then subsequently opened SEED, a macrobiotic restaurant in Paddington with his brother Craig Sams in 1968.[2] SEED Restaurant soon became popular ...

Stefan BötticherStefan Bötticher en 2018InformationsNaissance 1er février 1992 (32 ans)Leinefelde-WorbisNationalité allemandeÉquipe actuelle Team Erdgas.2012Équipes professionnelles 2012Team Erdgas.2012Principales victoires Champion du monde de vitesse (2013) Champion du monde de vitesse par équipes (2013)modifier - modifier le code - modifier Wikidata Stefan Bötticher (né le 1er février 1992 à Leinefelde) est un coureur cycliste allemand. Spécialiste des épreuves de vitesse...

Doni Tata PraditaDoni Tata Pradita di 250cc tahun 2008Kebangsaan IndonesiaLahir21 Januari 1991 (umur 33)Sleman, DI Yogyakarta, Indonesia Catatan statistik Karier Kejuaraan Dunia GP250Tahun aktif2007 – 2008 PabrikanYamahaJuara dunia0Klasemen 200828 Start Menang Podium Pole F. lap Poin 17 0 0 0 0 1 Karier Kejuaraan Dunia GP125Tahun aktif2005 – 2006 PabrikanYamahaJuara dunia0Klasemen 2006- Start Menang Podium Pole F. lap Poin 2 0 0 0 0 0 Doni Tata Pradita (lahir 21 Januari 1991) adalah ...









![{\displaystyle w_{i}={\frac {2}{\left(1-x_{i}^{2}\right)[P'_{n}(x_{i})]^{2}}}.\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c364b68e1c96b2bcc6462d0aee73e8dc7fc8cbb)













































![{\displaystyle w_{i}={\frac {x_{i}}{(n+1)^{2}[L_{n+1}(x_{i})]^{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02bb38888002be1f4533e00fa77c17525633e0b2)


![{\displaystyle w_{i}={\frac {2^{n-1}n!{\sqrt {\pi }}}{n^{2}[H_{n-1}(x_{i})]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f802b7bf4ffb5d3c9a7911f8aa0e23ea6b961e9)



![{\displaystyle w_{i}={\frac {1-x_{i}}{[nP_{n-1}(x_{i})]^{2}}}={\frac {1}{(1-x_{i})[P_{n-1}^{'}(x_{i})]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26c526a6bc426cffee3d15e9fa3feda1480c1d54)
![{\displaystyle E={\frac {2^{2n-1}n[(n-1)!]^{4}}{[(2n-1)!]^{3}}}f^{(2n-1)}(\xi ),\quad (-1<\xi <1).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/818430a0b932a1a79140635a32d980d680efb5e4)











![{\displaystyle w_{i}={\frac {2}{n(n-1)[P_{n-1}(x_{i})]^{2}}}\quad (x_{i}\neq \pm 1).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3176e2d0cc66326dce4d697e5c992fe7f8f78890)
![{\displaystyle E_{n}={\frac {-n(n-1)^{3}2^{2n-1}[(n-2)!]^{4}}{(2n-1)[(2n-2)!]^{3}}}f^{(2n-2)}(\xi ),\quad (-1<\xi <1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ceaabbaf9a5f511066493b51778786797b8126b0)




















