Ефект Гартмана

Ефект Гартмана — описує, що час затримки для квантово-тунельної частинки не залежить від товщини непрозорого бар'єру. Він названий на честь Томаса Гартмана, який відкрив його в 1962 році[1].

Огляд

Ефект Гартмана — це ефект тунелювання через бар'єр, де час тунелювання має тенденцію приймати постійне значення для досить довгих бар'єрів. Вперше був описаний Томасом Е. Гартманом у 1962 році[1]. Хоча цей ефект вперше було передбачено для квантових частинок, що керуються рівняннями Шредінгера, він також має місце для пакетів класичних електромагнітних хвиль, що тунелюють як еванесцентні хвилі через електромагнітні бар'єри[2]. Це трапляється тому, що рівняння Гельмгольца для електромагнітних хвиль і незалежне від часу рівняння Шредінгера мають однакову форму. Оскільки тунелювання — це хвильове явище, воно має місце для всіх видів хвиль — хвиль речовини, електромагнітних хвиль і навіть звукових хвиль. Отже, ефект Гартмана повинен існувати для всіх тунельних хвиль.

У фізиці не існує єдиного та загальноприйнятого визначення «часу тунелювання». Це відбувається тому, що час не є оператором у квантовій механіці, на відміну від інших величин, таких як положення та імпульс. Серед багатьох кандидатів на «час тунелювання» є (i) групова затримка або фазовий час, (ii) час перебування, (iii) час Лармора, (iv) час Бюттікера–Ландауера та (v) напівкласичний час[3][4]. Три з цих визначень часу тунелювання (групова затримка, час перебування та час Лармора) демонструють ефект Гартмана, в тому сенсі, що вони досягають постійного значення зі збільшенням товщини бар'єру. Якщо час тунелювання T залишається фіксованим при збільшенні довжини бар'єру L, то швидкість тунелювання v = L / T остаточно стане необмеженою. Таким чином, ефект Гартмана призводить до прогнозів аномально великих і навіть надсвітлових швидкостей тунелювання в межах товстих бар'єрів. Однак ймовірність передачі через такий бар'єр стає зникаюче малою, оскільки щільність ймовірності всередині бар'єру є експоненціально спадною функцією довжини бар'єру.

Експериментальна перевірка ефекту Гартмана

Експерименти з часом тунелювання з квантовими частинками, такими як електрони, є надзвичайно складними не лише через часові масштаби (атосекунди) і масштаби довжини (менші ніж нанометри), але й через можливу взаємодію з навколишнім середовищем, яка не має нічого спільного з самим процесом тунелюванням. У результаті єдині експериментальні спостереження ефекту Гартмана були засновані на електромагнітних аналогах квантового тунелювання. Перша експериментальна перевірка ефекту Гартмана була проведена Ендерсом і Німцом, які використовували мікрохвильовий хвилевід із звуженою областю, яка служила бар'єром для хвиль з частотою нижче граничної частоти в цій області[5][6]. Вони виміряли частотно-залежний фазовий зсув мікрохвиль безперервної хвилі, що передаються структурою. Вони виявили, що залежний від частоти фазовий зсув не залежить від довжини бар'єрної області. Оскільки групова затримка (фазовий час) є похідною від зсуву фази по частоті, така незалежність зсуву фази означає, що групова затримка не залежить від довжини бар'єру, і підтверджує ефект Гартмана. Вони також виявили, що виміряна групова затримка була меншою, ніж час проходження L / c для імпульсу, що поширюється зі швидкістю світла c через ту саму відстань бар'єру L у вакуумі. Звідси було зроблено висновок, що тунелювання еванесцентних хвиль є надсвітловим.

На оптичних частотах електромагнітні аналоги квантового тунелювання включають поширення хвилі у фотонних структурах із забороненою зоною та порушене повне внутрішнє відбиття на межі розділу між двома призмами, що знаходяться в тісному контакті. Шпільман та ін. послали лазерні імпульси тривалістю 12 фемтосекунд (FWHM) через смугу зупинки багатошарової діелектричної структури[7]. Було виявлено, що виміряна групова затримка не залежить від кількості шарів або, що еквівалентно, довжини фотонного бар'єру, таким чином підтверджуючи ефект Гартмана для тунелювання світлових хвиль. В іншому оптичному експерименті Лонгі та ін. лазерні імпульси тривалістю 380 пікосекунд були відправлені через смугу зупинки волокнистої решітки Брегга[en] (ВРБ)[8]. Експериментатори виміряли групову затримку переданих імпульсів для решіток довжиною 1,3 см, 1,6 см і 2 см і виявили, що затримка досягає постійного значення з довжиною L, і описується функцією tanh(qL), де q — константа з'єднання решітки. Це ще одне підтвердження ефекту Гартмана. Обчислена групова швидкість тунелювання була вищою, ніж швидкість еталонного імпульсу, що поширювався у волокні без бар'єру; швидкість також зростала з довжиною ВРБ або, що еквівалентно, відбивною здатністю.

У іншому підході до оптичного тунелювання Балку та Дютріо виміряли групову затримку, пов'язану з транспортуванням світла через невеликий проміжок між двома призмами[9]. Коли промінь світла, що проходить через призму, потрапляє на межу скло-повітря під кутом, що перевищує певний критичний кут, він зазнає повного внутрішнього відбиття, і енергія не передається в повітря. Однак, коли інша призма наближається дуже близько (в межах довжини хвилі) до першої призми, світло може тунелювати через щілину та переносити енергію в другу призму. Це явище відоме як порушення повного внутрішнього відображення (ППВВ) і є оптичним аналогом квантового тунелювання. Балку та Дютріо отримали групову затримку за допомогою вимірювання зсуву променя (відомого як зсув Ґуса–Генхена[en]) під час ППВВ. Вони виявили, що групова затримка досягає постійного значення при розділенні між призмами, таким чином підтверджуючи ефект Гартмана. Вони також виявили, що групові затримки були однаковими як для пропущених, так і для відбитих променів, результат, який прогнозується для симетричних бар'єрів.

Ефект Гартмана також спостерігався з акустичними хвилями. Ян та ін. поширювали ультразвукові імпульси через тривимірні фононні кристали з кульок карбіду вольфраму у воді[10]. Для частот всередині смуги зупинки вони виявили, що групова затримка досягає постійного значення для довжини зразка. Перетворюючи затримку на швидкість, використовуючи формулу v = L/T, вони виявили групову швидкість, яка зростає з довжиною зразка. В іншому експерименті Робертсон та ін. створили періодичну структуру акустичного хвилеводу з акустичною забороненою зоною для імпульсів звукової частоти[11]. Було виявлено, що всередині смуги зупинки акустична групова затримка була відносно нечутливою до довжини конструкції, що підтверджує ефект Гартмана. Крім того, групова швидкість зростала з довжиною і була більшою за швидкість звуку, явище, яке вони називають «подоланням звукового бар'єру».

Походження ефекту Гартмана

Чому час тунелювання частинки або хвильового пакета стає незалежним від довжини бар'єру для достатньо довгих бар'єрів? Походження ефекту Гартмана було загадкою протягом десятиліть. Якщо час тунелювання стає незалежним від довжини бар'єру, це означає, що хвильовий пакет прискорюється, коли бар'єр стає довшим. Він не тільки прискорюється, але й прискорюється саме на потрібну величину, щоб подолати збільшену відстань за той самий час. У 2002 році Герберт Вінфул[en] показав, що групова затримка для фотонної структури забороненої зони ідентична часу перебування, який пропорційний збереженій енергії в бар'єрі[12]. Насправді час перебування - це збережена енергія, поділена на вхідну потужність. У зоні зупинки електричне поле є експоненціально спадною функцією відстані. Запасена енергія пропорційна інтегралу від квадрата поля. Цей інтеграл, площа під спадною експонентою, стає незалежним від довжини для достатньо довгого бар'єру. Групова затримка досягає постійного значення, оскільки накопичена енергія досягає постійного значення. Він надав нове визначення груповій затримці в тунелюванні як час життя накопиченої енергії, що виходить через обидва кінці[13]. Ця інтерпретація групової затримки як тривалості також пояснює, чому групові затримки передачі та відбиття рівні для симетричного бар'єру. Він зазначив, що час тунелювання не є затримкою поширення і «не повинен бути пов'язаний зі швидкістю, оскільки еванесцентні хвилі не поширюються»[4]. В інших роботах Вінфул поширив свій аналіз на квантове (на відміну від електромагнітного) тунелювання та показав, що групова затримка дорівнює часу перебування плюс затримці самоперешкоди, обидва з яких пропорційні інтегральній щільності ймовірності і, отже, досягають постійного значення для заданої довжини бар'єра[14].

Примітки

  1. ↑ а б T. E. Hartman (1962). Tunneling of a wave packet. Journal of Applied Physics (англ.). 33 (12): 3427. Bibcode:1962JAP....33.3427H. doi:10.1063/1.1702424.
  2. ↑ J. J. Hupert and G. Ott (1966). Electromagnetic analog of the quantum-mechanical tunnel effect. American Journal of Physics (англ.). 34 (3): 3427. Bibcode:1966AmJPh..34..260H. doi:10.1119/1.1972898.
  3. ↑ E. H. Hauge and J. A. Stovneng (1989). Tunneling times: a critical review. Reviews of Modern Physics (англ.). 61 (4): 917. Bibcode:1989RvMP...61..917H. doi:10.1103/RevModPhys.61.917.
  4. ↑ а б H. Winful (2006). Tunneling time, the Hartman effect, and superluminality: A proposed resolution of an old paradox (PDF). Physics Reports[en] (англ.). 436 (1–2): 1—69. Bibcode:2006PhR…436….1W. doi:10.1016/j.physrep.2006.09.002. Архів оригіналу (PDF) за 25 березня 2023. Процитовано 14 вересня 2023. {{cite journal}}: Перевірте значення |bibcode= (довідка)
  5. ↑ A. Enders and G. Nimtz (1992). On superluminal barrier traversal. Journal de Physique I[en] (англ.). 2 (9): 1693—1698. Bibcode:1992JPhy1…2.1693E. doi:10.1051/jp1:1992236. {{cite journal}}: Перевірте значення |bibcode= (довідка)
  6. ↑ A. Enders and G. Nimtz (1993). Evanescent-mode propagation and quantum tunneling. Physical Review E (англ.). 48 (1): 632—634. Bibcode:1993PhRvE..48..632E. doi:10.1103/PhysRevE.48.632. PMID 9960633.
  7. ↑ C. Spielmann, R. Szipocs, A. Stingl, F. Krausz (1994). Tunneling of optical pulses through photonic band-gaps. Physical Review Letters (англ.). 73 (17): 2308—2311. Bibcode:1994PhRvL..73.2308S. doi:10.1103/PhysRevLett.73.2308. PMID 10057027.
  8. ↑ S. Longhi, M. Marano, P. Laporta, M. Belmonte (2001). Superluminal optical pulse propagation at 1.5 μm in periodic fiber Bragg gratings. Physical Review E (англ.). 64 (5): 055602. doi:10.1103/PhysRevE.64.055602. PMID 11736006.
  9. ↑ P. Balcou and L. Dutriaux (1997). Dual optical tunneling times in frustrated total internal reflection. Physical Review Letters (англ.). 78 (5): 851—854. Bibcode:1997PhRvL..78..851B. doi:10.1103/PhysRevLett.78.851.
  10. ↑ S. Yang, J. Page, Z. Liu, M. Cowan, C. Chan, P. Sheng (2002). Ultrasound tunneling through 3D phononic crystals. Physical Review Letters (англ.). 88 (10): 104301. Bibcode:2002PhRvL..88j4301Y. doi:10.1103/PhysRevLett.88.104301. PMID 11909358.
  11. ↑ W. Robertson, J. Ash, J. McGaugh (2002). Breaking the sound barrier: Tunneling of acoustic waves through the forbidden transmission region of a one-dimensional acoustic band gap array. American Journal of Physics (англ.). 70 (7): 689. Bibcode:2002AmJPh..70..689R. doi:10.1119/1.1477430.
  12. ↑ H. Winful (2002). Energy storage in superluminal barrier tunneling: origin of the "Hartman Effect". Optics Express[en] (англ.). 10 (25): 1491—1496. Bibcode:2002OExpr..10.1491W. doi:10.1364/OE.10.001491. PMID 19461683.
  13. ↑ H. Winful (2003). The meaning of group delay in barrier tunneling: a re-examination of superluminal group velocities. New Journal of Physics[en] (англ.). 8 (6): 101. arXiv:quant-ph/0601085. doi:10.1088/1367-2630/8/6/101.
  14. ↑ H. Winful (2003). Delay time and the Hartman effect in quantum tunneling. Physical Review Letters (англ.). 91 (26): 26041. Bibcode:2003PhRvL..91z0401W. doi:10.1103/PhysRevLett.91.260401. PMID 14754030.

Read other articles:

Mac OS 8

Mac OS 8sistema operativoLogoSviluppatoreApple Computer FamigliaClassic Mac OS(Proprietaria) Release iniziale8.0 (26 luglio 1997; 26 anni fa) Release corrente8.6 (10 maggio 1999; 24 anni fa) Piattaforme supportatePowerPC Tipo licenzaSoftware proprietario LicenzaProprietario Stadio di sviluppoNon supportato dal maggio 2001; 22 anni fa PredecessoreSystem 7 SuccessoreMac OS 9 Sito web Apple - Products - Mac OS 8.6, su apple.com. URL consultato l'11 gennaio 201...

 

Синелобый амазон

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

 

Phenylethylpyrrolidine

Phenylethylpyrrolidine Names Preferred IUPAC name 1-(2-Phenylethyl)pyrrolidine Identifiers CAS Number 6273-83-2 3D model (JSmol) Interactive image ChemSpider 364511 PubChem CID 411735 InChI InChI=1S/C12H17N/c1-2-6-12(7-3-1)8-11-13-9-4-5-10-13/h1-3,6-7H,4-5,8-11H2 SMILES c1c(cccc1)CCN2CCCC2 Properties Chemical formula C12H17N Molar mass 175.275 g·mol−1 Except where otherwise noted, data are given for materials in their standard state (at 25 °C [77 °F], 100 kPa)...

Queens Arcade

This article is about the shopping centre in Cardiff. For the Victorian shopping arcade in Belfast, see Queen's Arcade, Belfast. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Queens Arcade – news · newspapers · books · scholar · JSTOR (February 2024) (Learn how and when to remove this message) Shopping mal...

 

National Lampoon's Vacation

National Lampoon's VacationLa famiglia Griswold in una scena del film; da destra: Clark, Rusty, Audrey ed EllenTitolo originaleNational Lampoon's Vacation Lingua originaleinglese Paese di produzioneStati Uniti d'America Anno1983 Durata98 min Generecommedia RegiaHarold Ramis SceneggiaturaJohn Hughes; Harold Ramis (non accreditato); Chevy Chase (non accreditato) ProduttoreMatty Simmons Casa di produzioneWarner Bros. Distribuzione in italianoP.I.C. FotografiaVictor Kemper MontaggioPembroke J. He...

 

El Salvador at the 2000 Summer Olympics

Sporting event delegationEl Salvador at the2000 Summer OlympicsIOC codeESANOCEl Salvador Olympic CommitteeWebsitewww.teamesa.org (in Spanish)in SydneyCompetitors8 (4 men and 4 women) in 7 sportsFlag bearer Eva DimasMedals Gold 0 Silver 0 Bronze 0 Total 0 Summer Olympics appearances (overview)196819721976–198019841988199219962000200420082012201620202024 El Salvador competed at the 2000 Summer Olympics in Sydney, Australia, from 15 September to 1 October 2000. This was the nation's...

哈萨克斯坦总统

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言，清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日（哈薩克蘇維埃社會主義共和國總統） 哈萨克斯坦 哈萨克斯坦政府...

 

Henry Churchill de Mille

Henry Churchill de MilleLahir(1853-09-17)17 September 1853Washington, Carolina Utara, Amerika SerikatMeninggal10 Februari 1893(1893-02-10) (umur 39)Pompton Township, New Jersey, Amerika SerikatNama lainHenry C. de MillePekerjaanPengusaha, pengarang sandiwaraSuami/istriMatilda Beatrice Bebe Samuel ​ ​(m. 1876)​Anak3, termasuk William C. deMille dan Cecil B. DeMille Henry Churchill de Mille (17 September 1853 – 10 Februari 1893) adal...

 

Al Jabbar FC

Al Jabbar FC CirebonNama lengkapAl Jabbar Football ClubJulukanThe SchoolboysBerdiri1994 [1]PemilikSMK Al Jabbar CiledugManajerRetno Widodo[2]PelatihAde Lesmana[3]LigaLiga 32023Penyisihan grup (Liga 3 Jawa Barat Seri 1) Kostum kandang Kostum tandang Kostum ketiga Al Jabbar FC adalah klub sepak bola Indonesia yang berasal dari Pabuaran, Cirebon, Jawa Barat. Mereka berkompetisi di Liga 3 Jawa Barat. Al Jabbar FC sendiri dulunya hanya merupakan salah satu kegiatan ekstraku...

Tobias Ellwood

Tobias Ellwood Ketua Defence Select CommitteePetahanaMulai menjabat 29 Januari 2020PendahuluJulian LewisPenggantiPetahanaMenteri Tingkat Rendah Parlementer untuk PertahananMasa jabatan14 Juni 2017 – 26 Juli 2019Perdana MenteriTheresa MayPendahuluMark LancasterPenggantiJohnny MercerMenteri Tingkat Rendah Parlementer untuk Urusan Luar Negeri dan PersemakmuranMasa jabatan15 Juli 2014 – 14 Juni 2017Perdana MenteriDavid Cameron Theresa MayPendahuluHugh RobertsonPenggantiA...

 

Delaware County, Ohio

County in Ohio, United States County in OhioDelaware CountyCountyDelaware County Courthouse SealLocation within the U.S. state of OhioOhio's location within the U.S.Coordinates: 40°17′N 83°01′W / 40.28°N 83.01°W / 40.28; -83.01Country United StatesState OhioFoundedFebruary 10, 1808[1]Named forthe Delaware IndiansSeatDelawareLargest cityDelaware*Area • Total457 sq mi (1,180 km2) • Land443 sq mi (...

 

Nania Lain Dunia

Nania Lain DuniaGenre Drama Fiksi ilmiah Skenario Hilman Hariwijaya Maretha Abadi Cerita Hilman Hariwijaya Maretha Abadi SutradaraUmam A. P.Pemeran Dannia Salsabilla Ciccio Manassero Cassandra Lee Atiq Rachman Kenneth Santana Penggubah lagu temaMaudy AyundaLagu pembukaKini dan Selamanya oleh Maudy AyundaLagu penutupKini dan Selamanya oleh Maudy AyundaPenata musikBella MaritzaNegara asalIndonesiaBahasa asliBahasa IndonesiaJmlh. musim1Jmlh. episode25ProduksiProduser eksekutif Monika Rudi...

Colquitt County, Georgia

County in Georgia, United States Not to be confused with Colquitt, Georgia. County in GeorgiaColquitt CountyCountyColquitt County Courthouse in MoultrieLocation within the U.S. state of GeorgiaGeorgia's location within the U.S.Coordinates: 31°11′N 83°46′W / 31.19°N 83.77°W / 31.19; -83.77Country United StatesState GeorgiaFounded1856; 168 years ago (1856)Named forWalter Terry ColquittSeatMoultrieLargest cityMoultrieArea • ...

 

Jurnal Indonesia Sosial dan Teknologi

Jurnal Indonesia Sosial dan Teknologi (JIST) adalah publikasi ilmiah yang menerbitkan artikel-artikel penelitian asli serta tinjauan yang berkaitan dengan berbagai aspek sosial dan teknologi. Diterbitkan oleh CV. Publikasi Indonesia, JIST bertujuan untuk menyebarkan hasil penelitian dan pemikiran inovatif yang dapat berkontribusi pada perkembangan ilmu pengetahuan dan teknologi di Indonesia.Jurnal Indonesia Sosial dan Teknologi  Singkatan (ISO)JISTBahasaInggrisDisunting olehAbdurokhimDetail...

 

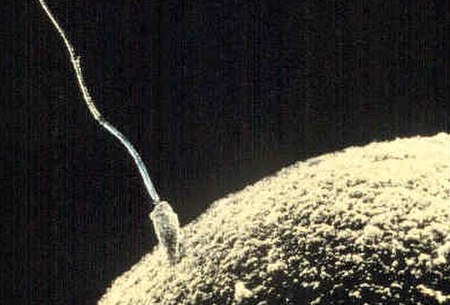
Gamete

A haploid sex cell Part of a series onSex Biological terms Sexual dimorphism Sexual differentiation Feminization Virilization Sex-determination system XY XO ZW ZO Temperature-dependent Haplodiploidy Heterogametic sex Homogametic sex Sex chromosome X chromosome Y chromosome Testis-determining factor Hermaphrodite Sequential hermaphroditism Simultaneous hermaphroditism Intersex (biology) Mating type Sexual reproduction Evolution of sexual reproduction Anisogamy Isogamy Germ cell Meiosis Gametog...

Stadionul Central (Vulcan)

Stadium in Romania Stadionul CentralAddressStrada Coroiești, Vulcan 336200LocationVulcan, RomaniaCoordinates45°22′36.8″N 23°18′23.6″E / 45.376889°N 23.306556°E / 45.376889; 23.306556OwnerMunicipality of VulcanOperatorCSM VulcanCapacity2,000SurfaceGrassOpened1955TenantsCSM Vulcan (1955–present) Central Stadium is a multi-use stadium in Vulcan, Hunedoara County. It is the home ground of CSM Vulcan. It can hold 2,000 people.[1][2] References...

 

Occupation of Alcatraz

American Indian protest in 1969 - 1971 Indians of All Tribes redirects here. For the Seattle organization, see United Indians of All Tribes. Occupation of AlcatrazPart of Red Power movement and political violence in the United States during the Cold WarMarkings from the occupation of Alcatraz as it appeared in 2010DateNovember 20, 1969 – June 11, 1971 (1969-11-20 – 1971-06-11) (1 year, 6 months and 22 days)LocationAlcatraz Island37°49′3...

 

Francesco Filippini

Francesco FilippiniFrancesco Filippini, potret diriLahir18 September 1853Brescia, ItaliaMeninggal6 Maret 1895Milan, ItaliaKebangsaanItaliaPendidikanPinacoteca TosioLuigi CampiniGiuseppe BertiniDikenal ataslanskapKarya terkenalLa sosta della contadina (1889), Il riposo della pastorella (1889), Il maglio (1889) o La strigliatura della canapa (1890)Gerakan politikScapigliaturaPenghargaanFumagalli Prize (1887)Mylius Prize (1890)Canoninca Prize (1889)[1] Prime nevi, 1889 Francesco Filippi...

Cornbread (album)

1967 studio album by Lee MorganCornbreadStudio album by Lee MorganReleasedEnd of January 1967[1]RecordedSeptember 18, 1965StudioVan Gelder Studio, Englewood Cliffs, New JerseyGenreSoul jazz, hard bopLength39:08LabelBlue NoteBST 84222ProducerAlfred LionLee Morgan chronology The Gigolo(1965) Cornbread(1967) Infinity(1965) Professional ratingsReview scoresSourceRatingAllMusic[2]The Penguin Guide to Jazz[3]The Rolling Stone Jazz Record Guide[4]DownBeat[...

 

Harry Holman

American actor (1862–1947) For the English footballer, see Harry Holman (footballer). This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Harry Holman – news · newspapers · books · scholar · JSTOR (January 2021) Harry HolmanHolman in 1909BornHarry James Holman(1862-03-15)March 15, 1862Conway, Missour...