Детермінований скінченний автомат
| ||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Lauh 343: Surat dari Oktavius untuk Kandidus mengenai pemasokan gandum, kulit hewan, dan urat daging Lauh Vindolanda pada saat ditemukan adalah dokumen tertulis tertua di Britania (tetapi kini dokumen tertulis tertua yang telah ditemukan di wilayah tersebut adalah Lauh Bloomberg). Lauh ini merupakan sumber informasi mengenai kehidupan di perbatasan utara Britania Romawi.[1][2][3] Tulisannya dibuat dalam lauh kayu yang tipis dengan tinta berbasis karbon. Lauh ini berasa...

Kaisarea FilipiCaesarea PhilippiReruntuhan Kaisarea FilipiLokasi di Dataran Tinggi GolanLokasiDataran Tinggi GolanKoordinat33°14′46″N 35°41′36″E / 33.246111°N 35.693333°E / 33.246111; 35.693333JenispemukimanSejarahBudayaRomawi Kaisarea Filipi (Inggris: Caesarea Philippicode: en is deprecated ; Yunani Kuno Καισαρεία Φιλίππεια; atau Caesarea Paneas; Yunani: Καισαρεία Πανειάς) adalah sebuah kota Romawi kuno yang terletak di ba...

Untuk kegunaan lain, lihat Maramureş. Peta Rumania dengan region Maramureş berwarna kuning Maramureş (dalam bahasa Rumania: Maramureș; Hongaria: Máramaroscode: hu is deprecated ; Latin: Marmatiacode: la is deprecated ; [Мармарощина / Marmaroshchyna, Мараморщина / Maramorshchyna, Марамуреш / Maramuresh] Error: {{Lang-xx}}: text has italic markup (help); bahasa Yiddi: מאַראַמאָראָש (maramurush)) adalah region geografis, historis dan etno-kult...

Politeknik Negeri NunukanJenisPoliteknik NegeriDidirikan24 September 2020Lembaga indukKementerian Pendidikan dan Kebudayaan Republik IndonesiaRektorArkas Viddy, SE, MM, Ph.DLokasiNunukan, Kalimantan Utara, IndonesiaSitus webpnn.ac.id Politeknik Negeri Nunukan disingkat PNN adalah perguruan tinggi negeri berbentuk politeknik di Kabupaten Nunukan, Kalimantan Utara. Nunukan adalah daerah yang berbatasan langsung dengan Malaysia. PNN baru berdiri tahun 2020, dan sebelumnya merupakan kampus binaan...

العلاقات الإريترية المارشالية إريتريا جزر مارشال إريتريا جزر مارشال تعديل مصدري - تعديل العلاقات الإريترية المارشالية هي العلاقات الثنائية التي تجمع بين إريتريا وجزر مارشال.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدول...

Reservoir in Los Angeles County, CaliforniaPuddingstone ReservoirSunsetPuddingstone ReservoirShow map of CaliforniaPuddingstone ReservoirShow map of the United StatesLocationLos Angeles County, CaliforniaCoordinates34°05′25″N 117°48′31″W / 34.09028°N 117.80861°W / 34.09028; -117.80861TypereservoirBasin countriesUnited StatesSurface area250 acres (1.0 km2)Surface elevation942 ft (287 m) Puddingstone Reservoir is a 250-acre (1 km²) a...

2020 film directed by Ashwath Marimuthu This article's plot summary may be too long or excessively detailed. Please help improve it by removing unnecessary details and making it more concise. (May 2021) (Learn how and when to remove this template message) Oh My KadavuleTheatrical release posterDirected byAshwath MarimuthuWritten byAshwath MarimuthuProduced byG. Dilli BabuAshok SelvanAbinaya SelvamStarring Ashok Selvan Ritika Singh Vani Bhojan CinematographyVidhu AyyannaEdited byBoopathi Selva...

Questa voce o sezione sull'argomento storia contemporanea non cita le fonti necessarie o quelle presenti sono insufficienti. Commento: I molti particolari come p.e.la forma a palline dei cristalli di gas Zyklon B merita decisamente una fonte. Diversi altri particolari se non fontati, possono apparire come una RO dello scrivente. Nessuna fonte sullo smantellamento dei campi di sterminio citati, manca se vogliamo essere precisi quello di sterminio di Treblinka e ridimensionato quello di M...

Pinacoteca di BreraCortile della Pinacoteca di Brera UbicazioneStato Italia LocalitàPalazzo di Brera Indirizzovia Brera, 28 - Milano e Via Brera 28, 20121 Milano Coordinate45°28′18.99″N 9°11′15.66″E / 45.471943°N 9.187683°E45.471943; 9.187683Coordinate: 45°28′18.99″N 9°11′15.66″E / 45.471943°N 9.187683°E45.471943; 9.187683 CaratteristicheTipopinacoteca Intitolato aPalazzo di Brera Istituzione1776 FondatoriMaria Teresa d'Austria Ape...

Jahanara Begumجہان آرا بیگمBegum SahibShahzadi SahibShahzadi dari Kekaisaran MughalPadshah BegumPeriode I1631-1638PendahuluMumtaz MahalPenerusRoshanara BegumPeriode II1669-1681PendahuluRoshanara BegumPenerusZinat-un-Nissa BegumInformasi pribadiKelahiran23 Maret 1614[1]Ajmer, Rajasthan, IndiaKematian16 September 1681(1681-09-16) (umur 67)Delhi, IndiaPemakamanNizamuddin Dargah, DelhiWangsaTimuridNama anumertaSahibat-uz-ZamaniAyahShah JahanIbuMumtaz MahalAgamaIslamShahzad...

American businesswoman and government official (1905–1995) Oveta Culp Hobby1st United States Secretary of Health, Education, and WelfareIn officeApril 11, 1953 – July 31, 1955PresidentDwight D. EisenhowerPreceded byHerself (Federal Security Agency Administrator)Succeeded byMarion B. FolsomAdministrator of the Federal Security AgencyIn officeJanuary 20, 1953 – April 11, 1953PresidentDwight D. EisenhowerPreceded byOscar EwingSucceeded byHerself (Health, Education and Wel...
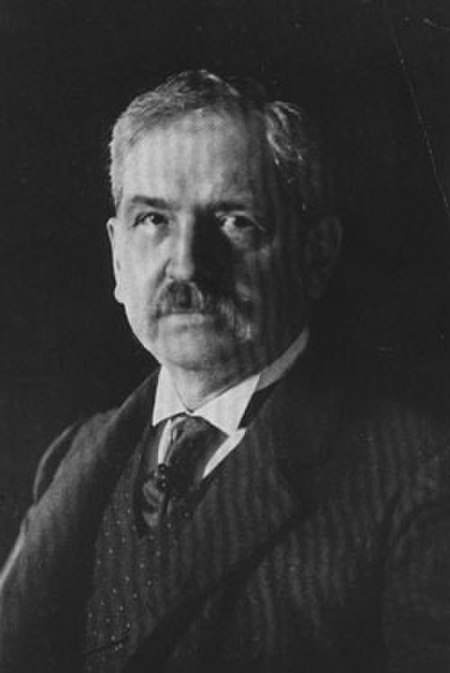
Charles Emory Smith 39° Direttore generale delle poste degli Stati UnitiDurata mandato21 aprile 1898 - 8 gennaio 1902 PredecessoreJames Albert Gary SuccessoreHenry Clay Payne Dati generaliPartito politicoPartito Repubblicano Firma Charles Emory Smith (Mansfield, 18 febbraio 1842 – Filadelfia, 19 gennaio 1908) è stato un politico e giornalista statunitense. Indice 1 Biografia 2 Note 3 Altri progetti 4 Collegamenti esterni Biografia Fu il trentanovesimo direttore generale delle po...

约翰·迪芬贝克John George Diefenbaker加拿大总理任期1957年6月21日—1963年4月22日前任路易·圣洛朗继任萊斯特·皮尔逊 个人资料出生(1895-10-18)1895年10月18日 加拿大安大略省诺伊施塔特(英语:Neustadt, Ontario)逝世1979年8月16日(1979歲—08—16)(83歲) 加拿大安大略省渥太華墓地加拿大萨斯喀彻温省萨斯卡通迪芬貝克加拿大中心(英语:Diefenbaker Canada Centre)政党加拿大進步保�...

American design strategist and academic Tom HardyAlma materAuburn UniversityOccupationDesigner, university teacherEmployerIBMSavannah College of Art and Design[edit on Wikidata] Tom Hardy (born 1946) is an American design strategist and Professor of Design Management at Savannah College of Art and Design (SCAD).[1][2] As corporate design advisor to Samsung Electronics (1996-2003) Hardy was instrumental in transforming their brand image from follower to innovation lead...

Mars PanjangTanggal16 Oktober 1934 – 22 Oktober 1935LokasiTiongkok, dari Jiangxi ke ShaanxiHasil Tentara Partai Komunis Tiongkok menghindari tentara Partai Nasionalis TiongkokPihak terlibat Partai Nasionalis Tiongkok dan para panglima perang yang bersekutu Partai Komunis TiongkokTokoh dan pemimpin Chiang Kai-shek Xue Yue Hans von Seeckt Bai Chongxi Mao Zedong Zhu De Zhou Enlai Peng Dehuai Lin BiaoKekuatan lebih dari 300.000 Tentara Merah Front Pertama: 86.000 (Oktober 1934) 7.000 (Oktober 1...

Ship class Alula in the port of Rotterdam Class overview BuildersSamsung Heavy Industries OperatorsHapag-Lloyd In service2011-present Planned9 Building0 Completed9 Active9 General characteristics TypeContainer ship Tonnage141,077 GT Length366 m (1,201 ft) Beam48.2 m (158 ft) Draught15.5 m (51 ft) PropulsionMAN B&W 12K98ME-7 Capacity13,296 TEU The A13 class is a series of 9 container ships originally built for the United Arab Shipping Company (UASC) ...

Protestantism in CanadaCathedral Church of St. James, TorontoOrientationChristianityPolityVariousRegionCanadaMembers29.2% of Canadians (8,654,850 as of 2001)[1] Protestantism in Canada has existed as a major faith in Canada ever since parts of northern Canada were colonized by the English. As of 2001, 29.2% of Canadians identified as Protestant.[1] According to a study by Pew Researchers published in 2013, 27% of Canadians are Protestant. Based on 2011 estimates, Protestant f...

1980 single by Charlie Daniels The Legend of Wooley SwampSingle by Charlie Danielsfrom the album Full Moon B-sideMoneyReleasedAugust 11, 1980GenreCountryLength4:18LabelEpicSongwriter(s)Charlie DanielsTom CrainJoel DiGregorioFred EdwardsJames W. MarshallCharles HaywardProducer(s)John BoylanCharlie Daniels singles chronology In America (1980) The Legend of Wooley Swamp (1980) Carolina (I Remember You) (1980) The Legend of Wooley Swamp is a song written, composed, and recorded by the Charlie Dan...

Marathon The Tokyo International Marathon was a marathon for male elite runners held in Tokyo, Japan, from 1980 until 2006. It actually consisted of two marathons - the Tokyo International Marathon which took place on even years, and Tokyo-New York Friendship International Marathon which took place on odd years. In the inaugural year, 1981, both marathons took place. However, because it was not possible to support two marathons a month apart in the same city, from 1982, the alternating format...

9th-century Iranian revolutionary leader For the director and writer, see Babak Khorramdin (director). Babak KhorramdinPersian: بابک خرمدینStatue of Babak Khorramdin in Babek city, Nakhchivan Autonomous Republic of Azerbaijan RepublicBorn795 or 798Ardabil, Abbasid Caliphate (present-day Iran)Diedprobably 7 January 838 (age 40 or 43)[1]Samarra, Abbasid Caliphate (present-day Iraq)Years active23 yearsKnown forLeader of the Khorram-DinānOpponentAbbasid CaliphateSpous...


















