Броунівський рух
|
Read other articles:
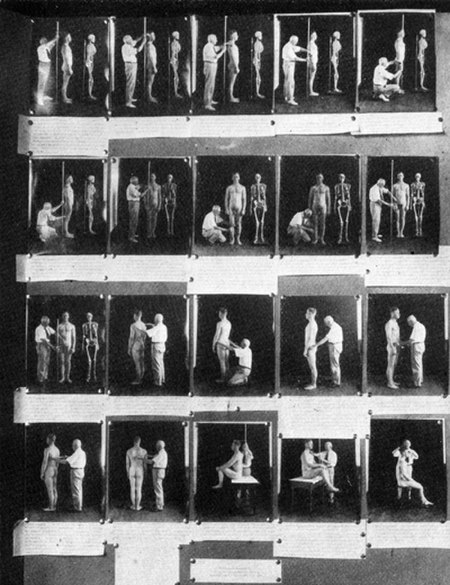
Exhibición de antropometría mostrada en la Segunda Exhibición Internacional de Eugenesia llevada a cabo entre el 22 de septiembre y el 22 de octubre de 1921 en el Museo Americano de Historia Natural en Nueva York. La eugenesia en Estados Unidos ha desempeñado un papel significativo en la historia y cultura de este país. La eugenesia, entendida como el estudio y práctica de la «mejora» de las características genéticas de las poblaciones humanas a través de la cría y esterilización...

EudibamusRentang fosil: Permian Awal, 284–279.5 jtyl PreЄ Є O S D C P T J K Pg N ↓ Restorasi Eudibamus Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Reptilia Subkelas: †Parareptilia Ordo: †Procolophonomorpha Famili: †Bolosauridae Genus: †EudibamusBerman et al., 2000 Spesies tipe †Eudibamus cursorisBerman et al., 2000 Eudibamus merupakan genus parareptil dari famili Bolosauridae yang hidup pada kala Perem Awal, pada 290 juta tahun lalu, yang ditemukan d...

العلاقات الغابونية الميكرونيسية الغابون ولايات ميكرونيسيا المتحدة الغابون ولايات ميكرونيسيا المتحدة تعديل مصدري - تعديل العلاقات الغابونية الميكرونيسية هي العلاقات الثنائية التي تجمع بين الغابون وولايات ميكرونيسيا المتحدة.[1][2][3][4][5...

Pour les articles homonymes, voir Téléphone (homonymie) et Radiophonie. La radiotéléphonie désigne les techniques de communication utilisant la radioélectricité, c'est-à-dire les ondes hertziennes pour transmettre la voix humaine. On utilise pour cela des émetteurs-récepteurs radioélectriques fixes et d'autres mobiles (montés sur un véhicule) ou portatifs (talkie-walkie) pour dialoguer, en passant éventuellement par des stations relais. Généralités Les « parents �...

Peta menunjukkan lokasi provinsi Negros Oriental Negros Oriental atau Negros Timur (Filipino:Silangang Negros, Cebuano: Sidlakang Negros) merupakan sebuah provinsi di Filipina. Ibu kotanya ialah Dumaguete City. Provinsi ini terletak di region Visayas Tengah. Provinsi ini memiliki luas wilayah 5.402 km² dengan memiliki jumlah penduduk 1.231.904 jiwa (2010) atau 246.380 tempat tinggal. Provinsi ini memiliki angka kepadatan penduduk 228 jiwa/km². Pembagian wilayah Secara administratif wil...

American politician For other people with the same name, see Richard Thomas (disambiguation). Richard ThomasMember of the U.S. House of Representativesfrom Pennsylvania's 3rd congressional districtIn officeMarch 4, 1795 to March 3, 1801Preceded bysee belowSucceeded byJoseph HemphillMember of the Pennsylvania Senatefrom the 9th districtIn office1791–1793Preceded bydistrict created Personal detailsBornDecember 30, 1744West Whiteland Township, Province of Pennsylvania, British Amer...

Rebecca, la prima mogliePaeseItalia Anno2008 Formatominiserie TV Generedrammatico, thriller, sentimentale Puntate2 Durata185 min (totale) Lingua originaleitaliano Dati tecniciB/N e a colori1,33:1 CreditiRegiaRiccardo Milani SoggettoDaphne du Maurier SceneggiaturaPatrizia Carrano Interpreti e personaggi Alessio Boni: Maxim de Winter Cristiana Capotondi: Jennifer de Winter Mariangela Melato: signora Danvers Omero Antonutti: Andrew Tomas Arana: Jack Favell Valentina Sperlì: Beatrice Lac...

Gunung LewotoloLetusan yang ditangkap oleh ESA sentinel-2 pada tanggal 29 November 2020Titik tertinggiKetinggian1.423 m (4.669 kaki)Koordinat8°16′17″S 123°30′20″E / 8.27144°S 123.50565°E / -8.27144; 123.50565Koordinat: 8°16′17″S 123°30′20″E / 8.27144°S 123.50565°E / -8.27144; 123.50565 GeografiGunung LewotoloLokasi Gunung Lewotolo di Pulau Lembata, NTTTampilkan peta Pulau TimorGunung LewotoloGunung Lewotolo (Nusa Te...

Gennady Ivanovich PadalkaLahir21 Juni 1958 (umur 65)Krasnodar, Uni SovietStatusPensiunKebangsaanRusiaPekerjaanPilotPenghargaanKarier luar angkasaAntariksawan RKAPangkatKolonel, Angkatan Udara RusiaTotal EVA10Lambang misi Gennady Ivanovich Padalka (bahasa Rusia: Гeннадий Иванович Падалка; lahir 21 Juni 1958) adalah seorang perwira Angkatan Udara Rusia dan antariksawan RKA. Padalka sekarang mencetak rekor dunia untuk waktu terlama di luar angkasa, dengan jangka w...

Cet article est une ébauche concernant l’agriculture et les Rosacées. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Consultez la liste des tâches à accomplir en page de discussion. Lady WilliamsPrésentationType Variété de pomme de culturemodifier - modifier le code - modifier Wikidata La « Lady Williams » est un cultivar de pomme issue d'un semis chanceux réalisé à Donnybrook, dans l'Ou...

Historical development of Lithuania For the book, see History of Lithuania (book). Part of a series on the History of Lithuania Prehistory Kunda culture Narva culture Neman culture Corded Ware culture Baltic tribes Yotvingia Amber Road / Aesti Lithuania proper Middle ages Duchy of Lithuania Grand Duchy of Lithuania Kingdom of Lithuania Jagiellonian period Early Modern era Early elective monarchy Deluge and decline Three partitions Polish–Lithuanian Commonwealth Partitions of the Polish–Li...

Emil WolkBorn1944 (age 79–80)New York City, New York, U.S.Years active1971-2018 Arnold Emil Wolk (born 1944) is an Anglo-American stage director and stage and screen actor. He was awarded the Laurence Olivier Award in 1988 (1987 season) as 'Best Actor in a Musical' for Kiss Me, Kate, sharing the award with co-star John Bardon.[1][2] Early years Emil Wolk was born in Brooklyn, New York to opera singer Jess Walters (Josuoh Wolk) and Emma Walters (née Defina). Wo...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

STS-128COSPAR ID2009-045ASATCAT no.35811 Akhir Misi STS-128 (penerbangan perakitan ISS 17A) adalah sebuah misi pesawat ulang alik ke Stasiun Luar Angkasa Internasional (ISS) yang diluncurkan pada 28 Agustus 2009. Pesawat Ulang Alik Discovery mengangkut Modul Logistik Serbaguna Leonardo sebagai beban angkut utamanya. Leonardo berisi sekumpulan eksperimen untuk mempelajari fisika dan kimia mikrogravitasi. Tiga aktivitas luar wahana dilakukan sepanjang misi ini untuk mengambil dan me...

كل ماتريده لولاWhatever Lola Wants (بالإنجليزية) معلومات عامةالصنف الفني فيلم رومانسي تاريخ الصدور 11 ديسمبر 2007مدة العرض 115 دقيقةاللغة الأصلية إنجليزيةعربيةالبلد المغرب، فرنسا، كندامواقع التصوير نيويورك — مصر — المغرب موقع الويب whateverlolawants-lefilm.com الطاقمالمخرج نبيل عيوشا...

Questa voce o sezione sull'argomento storia dell'arte non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Fibule Fibula di Braganza, British Museum Fibula è il nome latino della fibbia o della spilla, utilizzata in primo luogo per assicurare le vesti sulle spalle ed alla vita. Indice 1 Storia 2 Tipologia 3 Note 4 Voci correlate 5 Altri progetti 6 Collegamen...

أبو هلال العسكري معلومات شخصية الميلاد سنة 920 عسكر مكرم تاريخ الوفاة 395 هـ - 1005 م. مواطنة إيران الدولة العباسية الحياة العملية المهنة شاعر اللغات العربية أعمال بارزة جمهرة الامثال، وديوان المعاني [لغات أخرى] مؤلف:أبو هلال العسكري - ويكي ...

Військово-музичне управління Збройних сил України Тип військове формуванняЗасновано 1992Країна Україна Емблема управління Військово-музичне управління Збройних сил України — структурний підрозділ Генерального штабу Збройних сил України призначений для планува...

Brazilian businessman Luciano HangHang in 2019Born (1962-10-11) 11 October 1962 (age 61)Brusque, Santa Catarina, Brazil[1]Other namesVéio da Havan[2][3]Alma materBlumenau Regional UniversityOccupationBusinessmanKnown forCo-founder, Havan department store chainPolitical partyMDB (1985–2018)SpouseAndrea HangChildren3 Luciano Hang (born 11 October 1962)[1] is a Brazilian billionaire businessman, the co-founder of the Havan department store c...

Peter Bosz Bosz nel 2016 Nazionalità Paesi Bassi Altezza 178 cm Peso 75 kg Calcio Ruolo Allenatore (ex centrocampista) Squadra PSV Termine carriera 1º luglio 1999 - giocatore CarrieraSquadre di club1 1981-1984 Vitesse81 (2)1984-1985 AGOVV0 (0)1985-1988 RKC Waalwijk105 (4)1988-1991 Tolone93 (0)1991-1996 Feyenoord156 (6)1996-1997 JEF United33 (1)1997-1998 Hansa Rostock14 (0)1998-1999 NAC Breda26 (1)1999 JEF United15 (1)Nazionale 1991-1...






















