–ź–Ľ–≥–ĺ—Ä–ł—ā–ľ –ď–ĺ–Ņ–ļ—Ä–ĺ—Ą—ā–į ‚ÄĒ –ö–į—Ä–Ņ–į
|
Read other articles:

Chue LayChue Lay pada 2020Nama asalbahasa Burma: ŠÄĀŠÄľŠÄįŠÄłŠÄúŠÄĪŠÄłLahirSan Thaw Tar5 Oktober 1993 (umur 30)Thandwe, Negara Bagian Rakhine, MyanmarKebangsaanBurmaNama lainChue ChueAlmamaterUniversitas Yangon BaratPekerjaanPemeranTahun aktif2012‚ÄďkiniTinggi5 ft 4 in (1,63 m) Chue Lay (bahasa Burma: ŠÄĀŠÄľŠÄįŠÄłŠÄúŠÄĪŠÄł; nama lahir San Thaw Tar; lahir 5 Oktober 1993), dulunya disebut sebagai Nay Inzara (bahasa Burma: ŠÄĒŠÄĪŠÄ°ŠÄ•ŠÄĻŠÄáŠÄõŠÄ¨)...

Perdana Menteri Republik Arab MesirLambang MesirPetahanaMoustafa Madbouly[1]sejak 7 Juni 2018GelarYang MuliaMasa jabatanTidak ada batasanPejabat perdanaNubar PashaDibentuk28 Agustus 1878Situs webwww.cabinet.gov.eg Mesir Artikel ini adalah bagian dari seri Politik dan KetatanegaraanRepublik Arab Mesir Konstitusi (sejarah) Pemerintahan Presiden (daftar) Abdel Fattah el-Sisi Perdana Menteri (daftar) Sherif Ismail Kabinet Legislatif Parlemen Dewan Perwakilan Rakyat Ketua (daftar) Ali...

Jerrold Reinach ZachariasLahir23 Januari 1905Jacksonville, FloridaMeninggal16 Juli 1986(1986-07-16) (umur 81)KebangsaanAmerikaAlmamaterColumbia UniversityPenghargaanOersted Medal (1961)Karier ilmiahBidangFisikaInstitusiMassachusetts Institute of TechnologyDisertasiDependensi temperatur modulus Young untuk nikel (1934)Pembimbing doktoralShirley Leon QuimbyMahasiswa doktoralJohn G. King, Rainer Weiss Jerrold Reinach Zacharias (23 Januari 1905 – 16 Juli 1986) adalah se...

Fabrizio Miccoli Miccoli con il Palermo nel 2010 Nazionalità Italia Altezza 168[1] cm Peso 73[1] kg Calcio Ruolo Allenatore (ex attaccante) Termine carriera 16 dicembre 2015 - giocatore Carriera Giovanili 1987-1992 Scuola Calcio Lecce Club1992-1994 Milan1994-1996 Casarano Squadre di club1 1996-1998 Casarano57 (19)1998-2002 Ternana120 (32)2002-2003→ Perugia34 (9)2003-2004 Juventus25 (8)2004-2005 Fiorentina35 (12)2005-2007→ B...

ō•ōĪōßŔĄōĮŔą ŔÖŔąŔÜō≤ŔäŔĄŔäŔą ŔÖōĻŔĄŔąŔÖōßō™ ōīōģōĶŔäō© ōßŔĄŔÖŔäŔĄōßōĮ 5 ŔäŔąŔÜŔäŔą 1906(1906-06-05)ŔĀŔäŔÜŔäōßŔĄŔä ŔÖŔąŔÜŔĀŔäōĪōßō™Ŕą ōßŔĄŔąŔĀōßō© 3 ŔÜŔąŔĀŔÖō®ōĪ 1981 (ōĻŔÜ ōĻŔÖōĪ ŔÜōßŔáō≤ 75 ōĻōßŔÖōßŔč)ō™ŔąōĪŔäŔÜŔą ōßŔĄō∑ŔąŔĄ 1.73 ŔÖ (5 ŔāōĮŔÖ 8 ō®ŔąōĶō©) ŔÖōĪŔÉō≤ ōßŔĄŔĄōĻō® ŔÖōĮōßŔĀōĻ ōßŔĄō¨ŔÜō≥Ŕäō© ō•Ŕäō∑ōßŔĄŔäōß (18 ŔäŔąŔÜŔäŔą 1946‚Äď3 ŔÜŔąŔĀŔÖō®ōĪ 1981) ŔÖŔÖŔĄŔÉō© ō•Ŕäō∑ōßŔĄŔäōß (5 ŔäŔąŔÜŔäŔą 1906‚Äď18 ŔäŔąŔÜŔäŔą 1946) ōßŔĄŔÖō≥ŔäōĪō© ōßŔĄōßō≠ō™ōĪōßŔĀŔäō©...

Trains: Stations / Rapid transit / in UK Template‚ÄĎclass Trains¬†Portal This template is within the scope of WikiProject Trains, an attempt to build a comprehensive and detailed guide to rail transport on Wikipedia. If you would like to participate, you can visit the project page, where you can join the project and/or contribute to the discussion. See also: WikiProject Trains to do list and the Trains Portal.TrainsWikipedia:WikiProject TrainsTemplate:WikiProject Trainsrail transport articles...

Multi-parasport event in Sydney, Australia This article may need to be rewritten to comply with Wikipedia's quality standards, as Confusing sections, spelling and grammar mistakes, not up to the rigour of equivalent Olympics articles.. You can help. The talk page may contain suggestions. (August 2022) XI Paralympic GamesHost citySydney, New South Wales, AustraliaMottoPerformance, Power and PrideNations120Athletes3,881 (2,891 on foot, 990 on wheelchairs)Events551 in 18 sportsOpening18 OctoberC...

16th Chief Minister of Madhya Pradesh, India Babulal Gaur16th Chief Minister of Madhya PradeshIn office23 August 2004 ‚Äď 29 November 2005Preceded byUma BhartiSucceeded byShivraj Singh ChouhanMember of Madhya Pradesh Legislative AssemblyIn office1980 (1980)‚Äď2018 (2018)Preceded byLaxminarayan SharmaSucceeded byKrishna GaurConstituencyGovindpuraIn office1974 (1974)‚Äď1980 (1980)Preceded byConstituency establishedSucceeded bySatyanarayana AgarwalConstituencyBhopal ...

German army general (1892-1955) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Reiner Stahel ‚Äď news ¬∑ newspapers ¬∑ books ¬∑ scholar ¬∑ JSTOR (April 2016) (Learn how and when to remove this template message) Rainer StahelStahel in uniformBorn(1892-01-15)15 January 1892Bielefeld, German EmpireDied30 November 19...

US Supreme Court justice from 1958 to 1981 Potter StewartOfficial portrait, 1976Associate Justice of the Supreme Court of the United StatesIn officeOctober 14, 1958 ‚Äď July 3, 1981Nominated byDwight D. EisenhowerPreceded byHarold Hitz BurtonSucceeded bySandra Day O'ConnorJudge of the United States Court of Appeals for the Sixth CircuitIn officeApril 27, 1954 ‚Äď October 13, 1958Nominated byDwight D. EisenhowerPreceded byXenophon HicksSucceeded byLester LeFevre Cecil Persona...

Australian TV series or program The CircuitGenreDramaCreated by Ross Hutchens Kelly Lefever Written by Kelly Lefever Dot West Mitch Torres Beck Cole Directed by Steve Jodrell Catriona McKenzie Richard Frankland James Bogle Aaron Pedersen StarringAaron PedersenKelton PellTammy ClarksonMarta KaczmarekBill McCluskeyGary SweetComposerDavid BridieCountry of originAustraliaOriginal languageEnglishNo. of seasons2No. of episodes12ProductionRunning time53 minutesProduction companyMedia World Pictures...

śú¨śĘĚÁõģŚ≠ėŚú®šĽ•šłčŚēŹť°ĆԾƍęčŚćĒŚä©śĒĻŚĖĄśú¨śĘĚÁõģśąĖŚú®Ť®éŤęĖť†ĀťáĚŚįćŤ≠įť°ĆÁôľŤ°®Áúčś≥ē„Äā ś≠§śĘĚÁõģťúÄŤ¶ĀśďīŚÖÖ„Äā (2013ŚĻī1śúą1śó•)ŤĮ∑ŚćĒŚä©śĒĻŚĖĄŤŅôÁĮáśĘĚÁõģԾƜõīťÄ≤šłÄś≠•ÁöĄšŅ°śĀĮŚŹĮŤÉĹśúÉŚú®Ť®éŤęĖť†ĀśąĖśČ©ŚÖÖŤĮ∑śĪāšł≠śČ匹į„ÄāŤĮ∑Śú®śďīŚÖÖśĘĚÁõģŚĺĆŚįáś≠§ś®°śĚŅÁ߼ťô§„Äā ś≠§śĘĚÁõģťúÄŤ¶ĀŤ°•ŚÖÖśõīŚ§öśĚ•śļź„Äā (2013ŚĻī1śúą1śó•)ŤĮ∑ŚćŹŚä©Ť£úŚÖÖŚ§öśĖĻťĚĘŚŹĮťĚ†śĚ•śļźšĽ•śĒĻŚĖĄŤŅôÁĮáśĚ°ÁõģԾƜó†ś≥ēśü•ŤĮĀÁöĄŚÜÖŚģĻŚŹĮŤÉĹśúÉŚõ†ÁāļŚľāŤģģśŹźŚáļŤÄĆŤĘęÁ߼ťô§„ÄāŤáīšĹŅÁĒ®ŤÄÖÔľöŤĮ∑śźúÁīĘšłÄšłčśĚ°ÁõģÁöĄ...

Menara drum. Atraksi di menara drum. Lonceng besar yang terdapat di menara lonceng. Menara drum Beijing atau dalam bahasa Mandarin disebut Gulou (Hanzi: ťľďś•ľ; Pinyin: G«Ēl√≥u; harfiah: 'Menara drum'), terletak di ujung utara poros tengah Kota Bagian Dalam Beijing, di sebelah utara Jalan Di'anmen. Awalnya dibangun untuk seni musik, kemudian digunakan untuk mengumumkan waktu dan sekarang menjadi objek wisata. Menara lonceng Beijing atau dalam bahasa Mandarin disebut Zhonglou (Hanz...

Vatnaj√∂kull National ParkHikers journey to Hvannadalshnj√ļkur, the high peak of √Ėr√¶faj√∂kull.LocationSouth, southeast, east and northeast IcelandCoordinates64¬į30‚Ä≤N 17¬į00‚Ä≤W / 64.500¬įN 17.000¬įW / 64.500; -17.000Area14,141 square kilometres (5,460 sq mi)Established7 June 2008; 15 years ago (2008-06-07) UNESCO World Heritage SiteOfficial nameVatnaj√∂kull National Park - dynamic nature of fire and iceCriteriaNatural: (viii)Designa...

–£ —ć—ā–ĺ–≥–ĺ —ā–Ķ—Ä–ľ–ł–Ĺ–į —Ā—É—Č–Ķ—Ā—ā–≤—É—é—ā –ł –ī—Ä—É–≥–ł–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź, —Ā–ľ. –°–Ę–ü.–ě–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ —Ā—Ä–Ķ–ī–Ĺ–Ķ–Ļ —ā–ĺ—á–ļ–ł –Ņ–ĺ–Ņ–į–ī–į–Ĺ–ł—Ź (–ļ—Ä–į—Ā–Ĺ—č–Ļ —Ü–≤–Ķ—ā) –Ņ—Ä–ł —Ä–į–∑–Ī—Ä–ĺ—Ā–Ķ –Ĺ–Ķ–Ī–ĺ–Ľ—Ć—ą–ĺ–≥–ĺ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–į –≤—č—Ā—ā—Ä–Ķ–Ľ–ĺ–≤ (–Ņ–ĺ–Ņ–į–ī–į–Ĺ–ł–Ļ). –°—Ä–Ķ–ī–Ĺ—Ź—Ź —ā–ĺ—á–ļ–į –Ņ–ĺ–Ņ–į–ī–į–Ĺ–ł—Ź –ł–Ľ–ł —Ā—Ä–Ķ–ī–Ĺ—Ź—Ź —ā–ĺ—á–ļ–į –Ņ—Ä–ł—Ü–Ķ–Ľ–ł–≤–į–Ĺ–ł—Ź (–°–Ę–ü), –Ę–ĺ—á–ļ–į –Ņ—Ä–ł—Ü–Ķ–Ľ–ł–≤–į–Ĺ–ł—Ź ‚ÄĒ ¬ę–Į–Ī–Ľ–ĺ–ļ–嬼[1] ‚ÄĒ —ā–Ķ—Ä–ľ–ł–Ĺ, ...

People of Syrian origin living abroad Ethnic group Syrian diasporaTotal populationFrom 8 to possibly 15 million[1]Regions with significant populations Saudi Arabia449,314 (2022 census) [2]LanguagesNative: Syrian ArabicAlso Brazilian Portuguese, Dutch, Spanish, French, English, German, Swedish, Finnish, TurkishReligionIslam, Christianity, Druze, Syrian Jews Map of the Syrian diaspora around the world. Syria +1,000,000 +100,000 +1...

Formula Satu musim 1970 Juara Dunia Pembalap: Jochen Rindt Juara Dunia Konstruktor: Lotus-Ford Sebelum: 1969 Sesudah: 1971 Balapan menurut negaraBalapan menurut musim Jochen Rindt, juara dunia F1 anumerta yang pertama (dan satu-satunya sampai dengan saat ini). Formula Satu musim 1970 adalah sebuah ajang balap mobil yang termasuk dalam Kejuaraan Dunia FIA untuk balap mobil Formula Satu yang ke-21. Musim 1970 dimulai pada tanggal 7 Maret 1970, dan berakhir pada tanggal 25 Oktober setelah mempe...

Battle of the Spanish Civil War Battle of Ir√ļnPart of the Spanish Civil WarArmed civilians from the Republican side during the battleDateAugust 19 ‚Äď September 5, 1936LocationGipuzkoa, SpainResult Nationalist victoryBelligerents Spanish Republic NationalistsCommanders and leaders Antonio Ortega Manuel Crist√≥bal Errandonea Manuel Margarida Valdes Emilio Mola Colonel Alfonso Beorlegui Canet † Rafael Garc√≠a Vali√ĪoStrength Over 2,000[1]‚Äď3,000[2][3] Over 2...

Agostino Lodron (1540 ‚Äď 1570) √® stato un nobile italiano, conte della famiglia dei Lodron detti di Castellano, ultimo figlio maschio di Agostino Lodron e futuro ereditario, assieme ai fratelli, del Feudo di Castellano. Stemma dei Lodron Storia Figlio di Agostino Lodron e Maddalena Bagarotta Lodron, fu il primogenito di Agostino ed ebbe altri tre fratelli: Felice Lodron, Antonio e Giulia Lodron. Si arruol√≤ nell'esercito imperiale austriaco e mor√¨ circa nel 1570. Il suo cadavere fu portato...
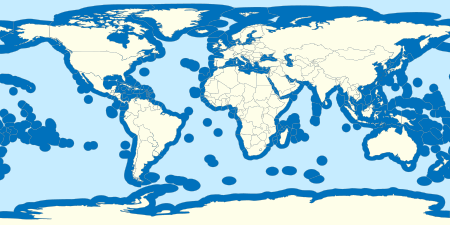
Wikipedia tiŠļŅng ViŠĽát ho√†n to√†n kh√īng chŠĽču tr√°ch nhiŠĽám vŠĽĀ nŠĽôi dung cŠĽßa nhŠĽĮng b√†i viŠļŅt vŠĽĀ luŠļ≠t ph√°p ńĎ∆įŠĽ£c ńĎńÉng tŠļ£i. B√†i viŠļŅt n√†y chŠĽČ nhŠļĪm v√†o mŠĽ•c ńĎ√≠ch cung cŠļ•p kiŠļŅn thŠĽ©c phŠĽē th√īng v√† kh√īng phŠļ£i l√† t∆į vŠļ•n ph√°p luŠļ≠t. C√°c v√Ļng ńĎŠļ∑c quyŠĽĀn kinh tŠļŅ tr√™n thŠļŅ giŠĽõi m√†u xanh ńĎŠļ≠m (ph√Ęn biŠĽát vŠĽõi v√Ļng biŠĽÉn quŠĽĎc tŠļŅ m√†u xanh nhŠļ°t) Trong luŠļ≠t biŠĽÉn quŠĽĎc tŠļŅ, v√Ļng ńĎŠļ∑c quyŠĽĀn kinh tŠļŅ (tiŠļŅng Anh: Exc...















































































