Ρ-алгоритм Полларда
|
Read other articles:

Halaman ini memuat artikel tentang huruf W dalam alfabet Latin. Untuk penggunaan lainnya, lihat W (disambiguasi). Lihat W, w di Wiktionary, kamus gratis. Alfabet Latindasar ISO AaBbCcDdEeFfGgHhIiJjKkLlMmNnOoPpQqRrSsTtUuVvWwXxYyZz lbs W adalah huruf Latin modern yang ke-23. Dalam bahasa Indonesia, huruf ini bernama we. Dalam Alfabet Fonetik Internasional, huruf W mewakili bunyi konsonan hampiran langit-langit belakang terbibirkan bersuara. Sejarah Buku cetakan tahun 1693 yang menggunakan u gan...

Немецкая колода — вариант 32-х или 36-карточной колоды, используемый для традиционных немецких карточных игр (например, скат). Немецкая колода развилась в XV веке в южной Германии из итало-испанской колоды. Кроме южных и восточных регионов Германии эта колода также испол�...

Telephone numbers in MontenegroLocation of Montenegro (dark green)LocationCountryMontenegroContinentEuropeRegulatorAgency of Telecommunications of MontenegroTypeOpenFormat0XX XXX XXXAccess codesCountry code+382International access00Long-distance0 This is a list of dialing codes by town in Montenegro. History Until Montenegro gained independence from Serbia and Montenegro, the nation was accessed through the international dialing code +381. The new dialing code +382 was introduced after indep...

UK Parliamentary by-election Furness The 1914 The Hartlepools by-election was held on 22 September 1914. The by-election was held due to the death of the incumbent Liberal MP, Sir Stephen Furness. It was won by the 67-year old Liberal candidate Sir Walter Runciman[1] who was unopposed due to a War-time electoral pact. Result Runciman 1914 The Hartlepools by-election [2] Party Candidate Votes % ±% Liberal Walter Runciman Unopposed N/A N/A Liberal hold References ^ Leigh Raymen...

Pour les articles homonymes, voir MacDonald. McDonald's Logo de McDonald's, dit des « arches dorées ». Création 15 mai 1940 (83 ans) (apparition du premier McDonald's en 1955) Fondateurs Ray Kroc(entreprise McDonald's). Personnages clés Ronald McDonald (personnage) Happy (personnage) Forme juridique Société anonyme Action NYSE : MCD Slogan « I’m lovin’ it » (international)« C'est tout ce que j'aime » (France)« Ça se passe comme ç...
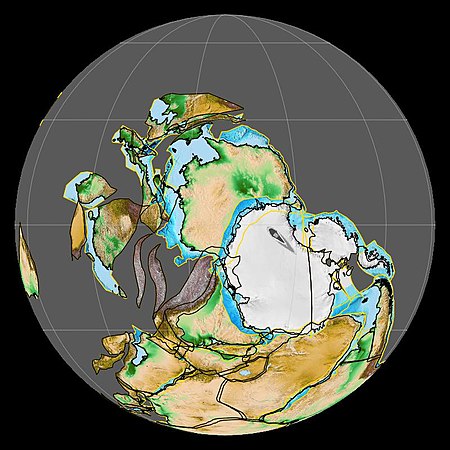
Peta dunia (Asia) pada subkala Katium, Ordovisium Akhir, 450 juta tahun lalu. Ordovisium Akhir merupakan kala ketiga dan terakhir dari periode Ordovisium, yang dimulai pada 458.4 juta tahun lalu, hingga 443.8 juta tahun lalu[1]. Dimulainya kala ini (sekaligus dimulainya subkala Sandbium) ditentukan dengan waktu munculnya spesies graptolit, Nemagraptus gracilis, di wilayah Rawa Sularp, Skane, Swedia.[2] Iklim Pada akhir periode Ordovisium, suhu Bumi mendingin, sehingga memulai ...

60th Air Mobility Wing Descrizione generaleNazione Stati Uniti ServizioUnited States Air Force TipoStormo da mobilità aerea Parte di Air Mobility Command ComandantiColonnelloThomas C. Pauly Fonti indicate nel testo Voci su unità militari presenti su Wikipedia KC-10A dello Stormo C-17A del 21st AS C-5M dello Stormo Il 60th Air Mobility Wing è uno stormo da mobilità aerea dell'Air Mobility Command, inquadrato nella Eighteenth Air Force. Il suo quartier generale è situato presso la Tra...

Dario Niccodemi nel 1924 Dario Niccodemi (Livorno, 27 gennaio 1874 – Roma, 24 settembre 1934) è stato un commediografo, sceneggiatore e capocomico italiano. Indice 1 Biografia 2 Teatro 3 Filmografia 3.1 Soggetti 4 Televisione 5 Opere 5.1 Teatro 5.2 Romanzi 5.3 Memorialistica 5.4 Libretti d'opera 6 Note 7 Bibliografia 8 Altri progetti 9 Collegamenti esterni Biografia Dario Niccodemi nacque a Livorno nel 1874. Quando era ancora bambino la sua famiglia si trasferì a Buenos Aires. Intorno ai ...

Angkatan Laut Kekaisaran RusiaРоссийский императорский флотRossiyskiy imperatorskiy flotLambang Angkatan Laut Kekaisaran RusiaDibentuk1696Negara Ketsaran Rusia Kekaisaran RusiaTipe unitAngkatan lautBagian dariAngkatan Bersenjata Kekaisaran RusiaPelindungSanto NikolasPertempuran Daftar pertempuran Perang Rusia-TurkiPerang Utara RayaPerang Rusia-PersiaPerang Rusia-SwediaPerang Tujuh TahunPerang Rusia-Turki IIPerang Rusia-Swedia IIPerang Rusia-Turki IIIPerang Rusi...

Prof. Hugo Junkers Prof. Hugo Junkers adalah seorang industriawan pesawat terbang berkebangsaan Jerman.[1] Dia lahir pada tanggal 3 Februari tahun 1859 di Rheidt, Prussia dan meninggal saat 3 Februari 1935 di Gauting, Munchen.[1][2] Junkers mendirikan pabrik pesawat di Dessau tahun 1910, pada tahun yang sama pula dia mematenkan desain sayap (pesawat) terbang.[2] Dia adalah orang yang merintis pembuatan pesawat udara dari bahan logam serta penerapan motor disel ...

Chronologies Données clés 1675 1676 1677 1678 1679 1680 1681Décennies :1640 1650 1660 1670 1680 1690 1700Siècles :XVe XVIe XVIIe XVIIIe XIXeMillénaires :-Ier Ier IIe IIIe Chronologies thématiques Art Architecture, Arts plastiques (Dessin, Gravure, Peinture et Sculpture), (), Littérature (), Musique (Classique) et Théâtre Ingénierie (), Architecture et () Politique Droit et () Religion (,) Sci...

此條目需要补充更多来源。 (2021年7月4日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:美国众议院 — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 美國眾議院 United States House of Representatives第118届美国国会众议院徽章 众议院旗...

密西西比州 哥伦布城市綽號:Possum Town哥伦布位于密西西比州的位置坐标:33°30′06″N 88°24′54″W / 33.501666666667°N 88.415°W / 33.501666666667; -88.415国家 美國州密西西比州县朗兹县始建于1821年政府 • 市长罗伯特·史密斯 (民主党)面积 • 总计22.3 平方英里(57.8 平方公里) • 陸地21.4 平方英里(55.5 平方公里) • ...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (أغسطس 2020) هذه الصفحة تعرض قائمة زملاء الجمعية الملكية المُنتخبين لعام 1723.[1] الزملاء �...

2020 American filmUpheaval: The Journey of Menachem BeginFilm PosterDirected byJonathan GruberWritten byJonathan GruberProduced byJonathan GruberRachel GreenbergGi OrmanBruce K. GouldBarry GurlandMonica GurlandIris MaidenbaumShalom MaidenbaumAlan MeltzerAmy MeltzerRaphael ShoreMicah SmithCinematographyShane Michael ColellaEdited byJohn AyalaMusic byCharlie BarnettProductioncompaniesHidden Light InstituteImagination ProductionsBegin Documentary Film, LLCDistributed byAbramoramaRelease dates Oc...

American college football season 2004 Appalachian State Mountaineers footballConferenceSouthern ConferenceRecord6–5 (4–3 SoCon)Head coachJerry Moore (16th season)Offensive schemeMultiple spreadBase defense4–3Home stadiumKidd Brewer StadiumSeasons← 20032005 → 2004 Southern Conference football standings vte Conf Overall Team W L W L No. 5 Furman $^ 6 – 1 10 – 3 No. 1...

City in Nevada, United States City in Nevada, United StatesMesquite, NevadaCityCity of MesquiteMain Street in January 2007, near City Hall FlagMotto(s): Escape, Momentarily[1]Location of Mesquite in Clark County, NevadaMesquiteLocation in the United StatesShow map of NevadaMesquiteMesquite (the United States)Show map of the United StatesCoordinates: 36°48′9″N 114°4′56″W / 36.80250°N 114.08222°W / 36.80250; -114.08222CountryUnited StatesStateNev...

Pour les articles homonymes, voir CED. États qui auraient fait partie de la Communauté européenne de défense selon le plan de René Pleven. La Communauté européenne de défense (CED) était un projet de création d'une armée européenne, avec des institutions supranationales, placées sous la supervision du commandant en chef de l'OTAN, qui était lui-même nommé par le président des États-Unis. Dans le contexte de la guerre froide, le projet, qui est esquissé en septembre-octobre...

Duta Besar Britania Raya untukRepublik HellenikLambang Britania RayaPetahanaKate SmithCMGsejak Januari 2017KediamanAthenaDitunjuk olehRatu Elizabeth IIPejabat perdanaEdward Dawkins Menteri Berkuasa Penuh PertamaDibentuk1833 Menteri Berkuasa Penuh 1862 Duta Luar Biasa 1943 Duta Besar Luar BiasaSitus webInggris dan Yunani Duta Besar Britania Raya untuk Yunani adalah perwakilan diplomatik terdepan Britania Raya di Yunani, dan kepala misi diplomatik Inggris di Yunani. Gelar resminya adalah D...

Ancient Egyptian greywacke palette Bull PaletteMaterialGreywackeHeight26.5 cmWidth14.5 cmCreatedc. 3100 BCDiscoveredbefore 2007EgyptPresent locationParis, Ile-de-France, France The Bull Palette (French: palette célébrant une victoire) is the fragment of an Ancient Egyptian greywacke palette, carved in low relief and used, at least in principle, as a cosmetic palette for the grinding of cosmetics. It is dated to Naqada III, the final two centuries of the fourth millennium BC, immediately pre...




















































![{\displaystyle [2^{k}+1;2^{k+1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c07eb73c96eb1f0c6352808214bf3c97ff0c9cad)


![{\displaystyle i\in [9;16]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b687c3c2dde795882a60407ed947ec55737911e)









































