Q-кулька
|
Read other articles:

Stasiun Anihata兄畑駅Stasiun Anihata pada 2021LokasiOkinotaira, Hachimantai-shi, Iwate-ken 028-7625JepangKoordinat40°6′56.7″N 140°52′58.9″E / 40.115750°N 140.883028°E / 40.115750; 140.883028Operator JR EastJalur■ Jalur HanawaLetak55.8 km dari KōmaJumlah peron1 peron sampingJumlah jalur1KonstruksiJenis strukturAtas tanahInformasi lainStatusTanpa stafSitus webSitus web resmiSejarahDibuka17 Oktober 1931Operasi layanan Stasiun sebelumnya JR East Stasiun b...

Stasiun Uedahara上田原駅Stasiun Uedahara, Oktober 2009LokasiUedahara, Ueda-shi, Nagano-ken 386-1102 JepangKoordinat36°23′25.85″N 138°13′17.8″E / 36.3905139°N 138.221611°E / 36.3905139; 138.221611OperatorUeda Electric RailwayJalur■ Bessho LineLetak2.9 km dari UedaJumlah peron1 peron pulauJumlah jalur2Informasi lainStatusStaf hanya beberapa jamKode stasiunBE05Situs webSitus web resmiSejarahDibuka17 Juni 1921PenumpangFY2015917 harian Lokasi pada pet...

Louis CartierLahir(1875-06-06)6 Juni 1875ParisMeninggal23 Juli 1942(1942-07-23) (umur 67)ParisKebangsaanPrancisPekerjaanPerajin perhiasan.KeluargaCartier Louis Cartier (1875-1942) ialah seorang pebisnis dan pembuat jam berkebangsaan Prancis yang dikenal akan rancangan jam tangannya yang anggun dan luar biasa. Ia adalah cucu dari Louis-François Cartier (pendiri Cartier SA) dan anak dari Alfred Cartier. Louis Cartier amat menggemari jam saku mekanis dan bercita-cita membuat jam sendiri. ...

Paus Anastasius IV. Paus Anastasius IV (menjabat 1153-54) mengangkat tiga kardinal dalam konsistori yang diadakan pada masa kepausannya.[1] Desember 1153 Gregorio della Suburra Alberto Jacopo Catatan dan referensi ^ Salvador Miranda. Cardinals of the 12th Century. The Cardinals of the Holy Roman Church. Diarsipkan dari versi asli tanggal 2015-09-19. Diakses tanggal 12 February 2019. Sumber The Cardinals of the Holy Roman Church Diarsipkan 2015-09-19 di Wayback Machine.

Cet article est une ébauche concernant l’histoire de France. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. « Paix d'Aix-la-Chapelle (1668) » redirige ici. Pour les autres significations, voir Traité d'Aix-la-Chapelle. Traité d’Aix-la-Chapelle Commémoration du traité d'Aix-la-Chapelle, plafond de la galerie des Glaces du château de Versailles. Données clés Type de traité Traité de paix...

العلاقات الإيطالية الوسط أفريقية إيطاليا جمهورية أفريقيا الوسطى إيطاليا جمهورية أفريقيا الوسطى تعديل مصدري - تعديل العلاقات الإيطالية الوسط أفريقية هي العلاقات الثنائية التي تجمع بين إيطاليا وجمهورية أفريقيا الوسطى.[1][2][3][4][5] مقارن...

Polish mathematician (1585–1652) Jan BrożekBornJan Brożek[citation needed]Kurzelów, PolandDied21 November 1652(1652-11-21) (aged 67)Bronowice Małe, PolandEducationKraków AcademyKnown forResearch on perfect numbers and geometryhoneycomb conjectureScientific careerFieldsMathematicsastronomymedicinepoetrymusicInstitutionsKraków Academy Jan Brożek or Johannes Broscius[a] (November 1585 – 21 November 1652) was the most prominent Polish mathematician of his era ...

Wild ChildPoster resmiSutradaraNick MooreProduser Tim Bevan Eric Fellner Diana Phillips Ditulis olehLucy DahlPemeran Emma Roberts Alex Pettyfer Georgia King Natasha Richardson Penata musikMichael PriceSinematograferChris SeagerPenyuntingSimon CozensPerusahaanproduksi StudioCanal Relativity Media Working Title Films DistributorUniversal PicturesTanggal rilis 15 Agustus 2008 (2008-08-15) (Inggris) Durasi97 menitNegara Inggris Amerika Serikat Prancis BahasaInggrisAnggaran$20 jutaP...

86th season in existence of Manchester United Manchester United 1967–68 football seasonManchester United1967–68 seasonThe European Cup trophy won by Manchester United displayed in the Manchester United museum, 1992.ChairmanLouis EdwardsManagerMatt BusbyFirst Division2ndFA CupThird RoundEuropean CupWinnersCharity ShieldSharedTop goalscorerLeague: George Best (28)All: George Best (32)Highest home attendance63,500 vs Tottenham Hotspur (27 January 1968)63,500 vs Real Madrid (24 April 1968)Low...

Salah satu sesi program berita di televisi Program berita atau acara berita, biasanya berisi liputan berbagai peristiwa berita dan informasi lainnya, apakah yang diproduksi secara lokal oleh stasiun radio atau televisi, atau oleh suatu jaringan penyiaran. Program berita juga bisa berisi materi tambahan seperti liputan olahraga, prakiraan cuaca, laporan lalulintas, komentar serta bahan lain yang oleh penyiar berita dianggap relevan dengan pendengar ataupun pemirsanya. Lihat pula Daftar stasiun...
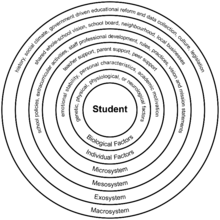
Human emotional need For the article about children's academic experiences, see School belonging. Part of a series onSociology History Outline Index Key themes Society Globalization Human behavior Human environmental impact Identity Industrial revolutions 3 / 4 / 5 Social complexity Social construct Social environment Social equality Social equity Social power Social stratification Social structure Perspectives Conflict theory Critical theory Structural functionalism Positivism Social constru...

Questa voce o sezione sugli argomenti avvocati italiani e politici italiani non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Questa voce sugli argomenti avvocati italiani e politici italiani è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del pr...

SebişKotaNegara RumaniaProvinsiProvinsi AradPemerintahan • Wali kotaPetru Gheorghe Feieş (Greater Romania Party (2004-8); Democratic Liberal Party (2008-))Luas • Total65,94 km2 (2,546 sq mi)Populasi (2002) • Total6.924Zona waktuUTC+2 (EET) • Musim panas (DST)UTC+3 (EEST)Situs webhttp://www.primariasebis.ro/ Sebiş (bahasa Hongaria: Borossebes) adalah sebuah kota di Provinsi Arad, bagian barat Transilvania, Rumania....

Breakfast cereal made from wheat For the underwear brand, see Shreddies Underwear. ShreddiesProduct typeBreakfast cerealOwnerPost Consumer BrandsProduced byPost Consumer (Canada)Nestlé (UK, Ireland)CountryCanadaIntroduced1939; 85 years ago (1939)Previous ownersNabiscoWebsitepostbrands.com/shreddies Shreddies are a breakfast cereal marketed in Canada, the United Kingdom and Ireland. It was first produced in Canada in 1939 by Nabisco. The Shreddies brand is held by Post ...

Mindy KalingKaling di Paleyfest pada 2013LahirVera Mindy Chokalingam24 Juni 1979 (umur 44)Cambridge, Massachusetts, ASTempat tinggalWest Hollywood, California, ASPendidikanBuckingham Browne & NicholsAlmamaterDartmouth CollegePekerjaanPemeran, comedian, penulisTahun aktif2003–sekarangKota asalBoston, Massachusetts, ASAnak1Karier komediMediaTunggal, televisi, film, bukuGenresatir, komedi improvisasional, komedi sketsa, komedi tunggalSubjekbudaya Amerika, budaya popDipengar...

Roman cuisine of pan braised artichokes Carciofi alla romanaCourseAntipasto, contornoPlace of originItalyRegion or stateLazioServing temperatureWarm or room temperatureMain ingredientsArtichokes, lesser calamint, parsley, garlic Media: Carciofi alla romana Carciofi alla romana (Italian: [karˈtʃɔːfi alla roˈmaːna]; lit. 'Roman-style artichokes') is a typical dish of Roman cuisine of pan braised artichokes. During spring-time in Rome, the dish is prepared in each h...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

Niederbronn-les-Bainscomune Niederbronn-les-Bains – Veduta LocalizzazioneStato Francia RegioneGrand Est Dipartimento Basso Reno ArrondissementHaguenau CantoneReichshoffen TerritorioCoordinate48°57′N 7°38′E / 48.95°N 7.633333°E48.95; 7.633333 (Niederbronn-les-Bains)Coordinate: 48°57′N 7°38′E / 48.95°N 7.633333°E48.95; 7.633333 (Niederbronn-les-Bains) Superficie31,45 km² Abitanti4 460[1] (2009) Densità141,81 ab....

British soldier and politician (1860–1949) Colonel The Right HonourableThe Earl of LucanGCVO KBE CB TD PC DLThe Earl of Lucan, c. 1896Member of Parliament for ChertseyIn office6 July 1904 – 8 January 1906Preceded byJohn Arthur FylerSucceeded byFrancis MarnhamConservative Chief Whip in the House of LordsIn office1929–1940Preceded byThe Earl of PlymouthSucceeded byThe Lord Templemore Personal detailsBorn13 December 1860Died20 April 1949(1949-04-20) (aged ...

آهنغركلا السفلي اهنگركلاسفلي - قرية - تقسيم إداري البلد إيران[1] المحافظة مازندران المقاطعة مقاطعة آمل الناحية ناحية دابودشت القسم الريفي قسم دابوي الجنوبی الريفي إحداثيات 36°36′00″N 52°29′00″E / 36.6°N 52.483333°E / 36.6; 52.483333 السكان التعداد السكاني 574 ن...







![{\displaystyle E_{\omega }=E+\omega \left[Q-{\frac {1}{2i}}\int d^{3}x(\phi ^{*}\partial _{t}\phi -\phi \partial _{t}\phi ^{*})\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e0c15078fa0b3b11534d83447d1aa12553a1122)
![{\displaystyle E=\int d^{3}x\left[{\frac {1}{2}}{\dot {\phi }}^{2}+{\frac {1}{2}}|\nabla \phi |^{2}+U(\phi ,\phi ^{*})\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06f924b5d8fbf26c9ceafb149b21f7f0155da092)


![{\displaystyle E_{\omega }=\int d^{3}x\left[{\frac {1}{2}}|{\dot {\phi }}-i\omega \phi |^{2}+{\frac {1}{2}}|\nabla \phi |^{2}+{\hat {U}}_{\omega }(\phi ,\phi ^{*})\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d358aad3090c3ff7158608083886f0b63fccab22)














