Q-аналог
|
Read other articles:

Asparagaceae Asparagus officinalis Klasifikasi ilmiah Kerajaan: Plantae (tanpa takson): Angiospermae (tanpa takson): Monokotil Ordo: Asparagales Famili: AsparagaceaeJuss. (1789) Genus Lihat teks Suku asparagus-asparagusan atau Asparagaceae adalah salah satu suku anggota tumbuhan berbunga. Menurut Sistem klasifikasi APG II suku ini dimasukkan ke dalam bangsa Asparagales, klad Monokotil. Pengertian suku ini dapat dilihat dari arti luas (sensu lato) maupun arti sempit (sensu stricto) yang kedua...
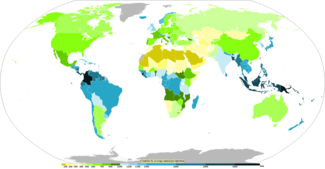
Untuk kegunaan lain, lihat Presipitasi (disambiguasi).Rata-rata curah hujan bulanan Curah hujan tahunan tiap negara Dalam meteorologi, presipitasi atau curah hujan (juga dikenal sebagai satu kelas dalam hidrometeor, yang merupakan fenomena atmosferik) adalah setiap produk dari pengembunan uap air di atmosfer. Ini terjadi ketika atmosfer (yang merupakan suatu larutan gas raksasa) menjadi jenuh dan air kemudian terembun dan keluar dari larutan tersebut (tercurah hujan).[1] Udara menjadi...

Association football club in Romania This article is about the football club founded in 1922 and dissolved in 2015. For the current club, see CS Gloria Bistrița-Năsăud. For other uses, see Gloria Bistrița. Football clubGloria BistrițaFull nameAsociația Club de Fotbal Gloria BistrițaNickname(s)Vampirii albaștri (The Blue Vampires)Alb-albaștrii (The White and Blues)Glorioșii (The Glorious Ones)Echipa lui Dracula (Dracula's Squad)Short nameGloriaFounded6 July 1922; 101 years ag...

Atypical antipsychotic TenilapineINN: tenilapineIdentifiers IUPAC name (2E)-[5-(4-Methyl-1-piperazinyl)-9H-bisthieno[3,4-b:3',4'-e]azepin-9-ylidene]acetonitrile CAS Number82650-83-7 Y[PubChem]PubChem CID6450478ChemSpider4953083UNIID0U312O2BEChEMBLChEMBL2105472Chemical and physical dataFormulaC17H16N4S2Molar mass340.46 g·mol−13D model (JSmol)Interactive image SMILES CN1CCN(CC1)C2=NC3=CSC=C3/C(=C/C#N)/C4=CSC=C42 InChI InChI=1S/C17H16N4S2/c1-20-4-6-21(7-5-20)17-15-10-22-8-13...

Aibetsu 愛別町KotaprajaBalai Kota Aibetsu BenderaEmblemLokasi Aibetsu di Hokkaido (Subprefektur Kamikawa)AibetsuLokasi di JepangKoordinat: 43°54′N 142°35′E / 43.900°N 142.583°E / 43.900; 142.583Koordinat: 43°54′N 142°35′E / 43.900°N 142.583°E / 43.900; 142.583NegaraJepangWilayahHokkaidoPrefektur Hokkaido (Subprefektur Kamikawa)DistrikKamikawa (Ishikari)Pemerintahan • WalikotaFukujirō YabeLuas • To...

العلاقات السيشلية الكورية الشمالية سيشل كوريا الشمالية سيشل كوريا الشمالية تعديل مصدري - تعديل العلاقات السيشلية الكورية الشمالية هي العلاقات الثنائية التي تجمع بين سيشل وكوريا الشمالية.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة �...

LATAM Airlines Paraguay IATA ICAO Kode panggil LA LAP PARAGUAYA Didirikan17 November 1962 (sebagai LAP) 1 September 1996 (sebagai TAM Mercosur) 5 Mei 2016 (sebagai LATAM Paraguay)PenghubungBandar Udara Internasional Silvio PettirossiProgram penumpang setiaLATAM PassAliansiStar Alliance (2010-2014; afiliasi)Armada5Tujuan3Perusahaan indukLATAM Airlines GroupKantor pusatAsunción, ParaguayTokoh utamaEnrique Alcaide (CEO)Situs webwww.latam.com/es_py/ Transportes Aereos del Mercosur S.A, d/b/a LAT...

Francisco Romero (1891–1962) was a Latin American philosopher who spearheaded a reaction against positivism. Biography Romero was born in Seville, Spain, but spent much of his adult life in Latin America, especially Argentina, where he emigrated in 1904.[1][2] He entered the Argentine army in 1910 and retired with the rank of major in 1931.[2] He became a friend of the Argentine philosopher Alejandro Korn, and when he left military service he took over Korn's profes...

Come leggere il tassoboxMelaleuca alternifolia Stato di conservazione Specie non valutata Classificazione APG IV Dominio Eukaryota Regno Plantae (clade) Angiosperme (clade) Mesangiosperme (clade) Eudicotiledoni (clade) Eudicotiledoni centrali (clade) Superrosidi (clade) Rosidi (clade) Eurosidi (clade) Eurosidi II Ordine Myrtales Famiglia Myrtaceae Sottofamiglia Myrtoideae Tribù Melaleuceae Genere Melaleuca Specie M. alternifolia Classificazione Cronquist Dominio Eukaryota Regno Plantae Sott...

American racing driver (1928–1993) Hap SharpBorn(1928-01-01)January 1, 1928Tulsa, OklahomaDiedMay 7, 1993(1993-05-07) (aged 65)San Martín de los Andes, ArgentinaFormula One World Championship careerNationality AmericanActive years1961–1964Teamsprivate Cooper, non-works Lotus and BrabhamEntries6Championships0Wins0Podiums0Career points0Pole positions0Fastest laps0First entry1961 United States Grand PrixLast entry1964 Mexican Grand Prix The Chaparral 2F Sharp shared with Phil Hill...

Pulau BiraNegaraIndonesiaGugus kepulauanKepulauan SeribuProvinsiDKI JakartaKabupatenKepulauan SeribuLuas0,14 km²Populasi- Pulau Bira adalah sebuah pulau yang terletak di Kepulauan Seribu di Daerah Khusus Ibukota Jakarta, Indonesia. Kawasan Pulau Bira terbagi atas Pulau Bira Besar dan Pulau Bira Kecil. Sejarah Awalnya Pulau Bira merupakan sebuah pulau pribadi milik keluarga Presiden RI ke 2, Soeharto yang mulai diresmikan pada tanggal; 13 September 1997 oleh Umar Wirahadikusumah. Sebagai...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

此條目可能包含不适用或被曲解的引用资料,部分内容的准确性无法被证實。 (2023年1月5日)请协助校核其中的错误以改善这篇条目。详情请参见条目的讨论页。 各国相关 主題列表 索引 国内生产总值 石油储量 国防预算 武装部队(军事) 官方语言 人口統計 人口密度 生育率 出生率 死亡率 自杀率 谋杀率 失业率 储蓄率 识字率 出口额 进口额 煤产量 发电量 监禁率 死刑 国债 ...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要編修,以確保文法、用詞、语气、格式、標點等使用恰当。 (2013年8月6日)請按照校對指引,幫助编辑這個條目。(幫助、討論) 此條目剧情、虛構用語或人物介紹过长过细,需清理无关故事主轴的细节、用語和角色介紹。 (2020年10月6日)劇情、用語和人物介紹都只是用於了解故事主軸,輔助�...

HelfensteinCountryCounty of Helfenstein[disambiguation needed]FoundedAround 1100FounderEberhard of HelfensteinCurrent headErnst Heinrich von HelfensteinFinal rulerGeorg I (Helfenstein-Blaubeuren)/Rudolph II (Helfenstein-Wiesensteig)TitlesCount, Freiherr, HerrDissolutionHelfenstein-Blaubeuren in 1517, Helfenstein-Wiesensteig on 20 September 1627Cadet branchesHelfenstein-Blaubeuren, Helfenstein-Wiesensteig The House of Helfenstein was a German noble family during the High and Late Midd...

Untuk pengertian lain, silakan lihat Grand Rapids Pemandangan Grand Rapids dari udara Grand Rapids ialah kota besar di Michigan barat, Amerika Serikat. Mantan Presiden Amerika Serikat Gerald Ford besar dan dimakamkan di Grand Rapids. Grand Rapids juga tempat kelahiran Amway dan rantai penyimpanan Meijer. Grand Rapids ialah county seat Kent County. Merupakan kota terbesar ke-2 di negara bagian ini, setelah Detroit. Kota ini memiliki banyak daya tarik, termasuk Frederik Meijer Gardens and Sculp...

Union state in the American Civil War Union states in the American Civil War California Connecticut Delaware Illinois Indiana Iowa Kansas Maine Maryland Massachusetts Michigan Minnesota Nevada New Hampshire New Jersey New York Ohio Oregon Pennsylvania Rhode Island Vermont West Virginia Wisconsin Dual governments Kentucky Missouri Virginia West Virginia Territories and D.C. Arizona Colorado Dakota District of Columbia Idaho Indian Territory Montana Nebraska New Mexico Utah Washington vte The s...

Slippery When WetAlbum studio karya Bon JoviDirilis18 Agustus 1986DirekamLittle Mountain, Vancouver, KanadaGenreHard rock, glam metalDurasi43:42LabelMercuryProduserBruce FairbairnKronologi Bon Jovi 7800°Fahrenheit(1985)7800°Fahrenheit1985 Slippery When Wet(1986) New Jersey(1988) Singel dalam album Slippery When Wet You Give Love a Bad NameDirilis: 23 Juli 1986 Livin' On a PrayerDirilis: 31 Oktober 1986 Wanted Dead or AliveDirilis: 2 Maret 1987 Never Say GoodbyeDirilis: 15 Juni 1987 New ...

![{\displaystyle [n]_{q}={\frac {1-q^{n}}{1-q}}=1+q+q^{2}+\ldots +q^{n-1}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/54905ab6a45450b4e798ef991a9f7c6cd65711db)
![{\displaystyle {\begin{aligned}{\big [}n]_{q}!&=[1]_{q}\cdot [2]_{q}\cdots [n-1]_{q}\cdot [n]_{q}\\[6pt]&={\frac {1-q}{1-q}}\cdot {\frac {1-q^{2}}{1-q}}\cdots {\frac {1-q^{n-1}}{1-q}}\cdot {\frac {1-q^{n}}{1-q}}\\[6pt]&=1\cdot (1+q)\cdots (1+q+\cdots +q^{n-2})\cdot (1+q+\cdots +q^{n-1}).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e9aca08867b8fd46c5c717a2a8aca39c294faf0)
![{\displaystyle \sum _{w\in S_{n}}q^{{\text{inv}}(w)}=[n]_{q}!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1fdbf42b3988d54e8a3997462fbf86ee1efc88fa)

![{\displaystyle [n]_{q}!={\frac {(q;q)_{n}}{(1-q)^{n}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee6a1e12939e2d9c21567ce00527543674ba70d6)
![{\displaystyle {\binom {n}{k}}_{q}={\frac {[n]_{q}!}{[n-k]_{q}![k]_{q}!}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e2d350cdfdff22544fac702c5d397578cde0d44)
![{\displaystyle e_{q}^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{[n]_{q}!}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab5943d719a2f4615fdd2a4a3da4cbd362260756)

