Флексагон
| |||||||||||||||||||||||
Read other articles:

Lukisan karya Walter Langley, Between The Tides, 1901, seorang nelayan mengenakan smok Gaun smok (bahasa Inggris: smock atau smock-frock) adalah pakaian luar yang secara tradisional dikenakan oleh pekerja pedesaan, terutama penggembala dan penarik gerobak, di beberapa bagian Inggris dan Wales sepanjang abad ke-18. Saat ini, kata smok mengacu pada pakaian luar longgar yang dikenakan untuk melindungi pakaian seseorang, misalnya oleh seorang pelukis. Baju tradisional amok terbuat dari linen atau...

Menurut legenda, Raja Abgar menerima Gambar dari Edessa, yang memuat gambar wajah Yesus. Gambar dari Edessa (Inggris: Image of Edessacode: en is deprecated ) menurut tradisi Kristen adalah relikwi kudus yang berupa kain berbentuk bujursangkar atau persegi panjang yang secara ajaib memuat cetakan wajah Yesus. Merupakan ikon (gambar) pertama. Dalam gereja Ortodoks Timur dan juga dalam bahasa Inggris, gambar ini dikenal sebagai Mandylion. Menurut legenda, ketika Konon Yesus Kristus masih hidup, ...

Asosiasi Sepak Bola Kerajaan BelandaUEFADidirikan1889Kantor pusatZeistBergabung dengan FIFA1904Bergabung dengan UEFA1954PresidenMichael van PraagWebsitewww.knvb.nl Asosiasi Sepak Bola Kerajaan Belanda (Belanda: Koninklijke Nederlandse Voetbalbond (KNVB)code: nl is deprecated ) adalah badan pengendali sepak bola di Belanda. Kompetisi Badan ini menyelenggarakan beberapa kompetisi di Belanda, yakni: Eredivisie (Liga Divisi Utama Belanda) Liga Divisi Satu Belanda Piala Asosiasi Sepak Bola Kerajaa...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. Google Doodle interaktif mengenai Pac-Man sejak tahun 2010 yang akan muncul ketika pengguna mencari google pacman atau play pacman. Perusahaan teknologi Google telah menambahkan easter egg pada berbagai produk dan layanannya, seperti Google Penelusuran...

Questa voce o sezione tratta di un conflitto in corso. Le informazioni possono pertanto cambiare rapidamente con il progredire degli eventi. Se vuoi scrivere un articolo giornalistico sull'argomento, puoi farlo su Wikinotizie. Non aggiungere speculazioni alla voce. Guerra civile sirianaparte della primavera araba e dell'inverno araboSituazione militare al novembre 2023: Forze governative Coalizione d'opposizione (con truppe della Tu...

RestaurantJoe's ShanghaiXiaolongbao from Joe's ShanghaiRestaurant informationEstablished1995Owner(s)Joe SiPrevious owner(s)Barbara MatsumuraHead chefJoe SiFood typeShanghai cuisineWebsitewww.joeshanghairestaurants.com Joe's Shanghai (simplified Chinese: 鹿鸣春; traditional Chinese: 鹿鳴春; pinyin: Lù Míng Chūn) is a chain of seven Shanghainese restaurants in the United States and Japan. The original location was opened by restaurateur Mei Ping Barbara Matsumura and chef ...

SI27Stasiun Higashi-Hannō東飯能駅Pintu masuk barat Stasiun Higashi-Hannō, Mei 2006Lokasi1-5 Azuma-chō, Hannō, Saitama(埼玉県飯能市東町1丁目)JepangOperator JR East Seibu Railway Jalur ■ Jalur Hachikō Jalur Seibu Ikebukuro Jumlah peron1 peron samping, 1 peron pulauInformasi lainKode stasiunSI27SejarahDibuka1931PenumpangFY20135,583 (JR East, hanya keberangkatan), 5,478 (Seibu) per hari Sunting kotak info • L • BBantuan penggunaan templat ini Stasiun Higashi...

2020 Texas Democratic presidential primary 2020 Texas Democratic presidential primary ← 2016 March 3, 2020 2024 → ← TNUT →260 delegates (228 pledged, 32 unpledged)to the Democratic National ConventionThe number of pledged delegates won is determined by the popular vote Candidate Joe Biden Bernie Sanders Home state Delaware Vermont Delegate count 113 99 Popular vote 725,562 626,339 Percentage 34.6% 29.9% Candidate Michael...

F. C. Burnand BiografiKelahiran29 November 1836 Kematian21 April 1917 (80 tahun) Data pribadiPendidikanEton College Trinity College KegiatanPekerjaanwartawan, penulis, penyunting, librettist, barrister Penghargaan Knight Bachelor Tanda tangan [[Berkas: |220x250px|alt=]] Sir Francis Cowley Burnand (29 November 1836 – 21 April 1917), yang lebih dikenal sebagai F. C. Burnand, adalah seorang penulis sandiwara dan penulis komika asal Inggris. Ia dikenal sebaga...
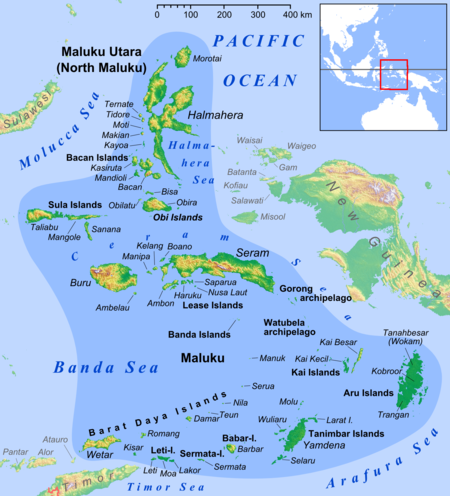
Sea in the Australasian Mediterranean Halmahera SeaLaut Halmahera (Indonesian)Location of the Halmahera Sea within Southeast AsiaHalmahera SeaCoordinates1°S 129°E / 1°S 129°E / -1; 129TypeSeaBasin countriesIndonesiaSurface area95,000 km2 (37,000 sq mi) The Halmahera Sea is a regional sea located in the central eastern part of the Australasian Mediterranean Sea. It is centered at about 1°S and 129°E and is bordered by the Pacific Ocean to ...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

Вишну со своей супругой Лакшми в храме Нараяна-Тирумала в Шрикакуламе (Андхра-Прадеш) Махави́шну (букв. «Великий Вишну», IAST: Mahāviṣṇu, санскр. विष्णु) — «проникающий во всё», «всеобъемлющий», «везде присутствующий» Господь, почитающийся в шри-вайшнавизме и других тра...

هنودمعلومات عامةنسبة التسمية الهند التعداد الكليالتعداد قرابة 1.21 مليار[1][2]تعداد الهند عام 2011ق. 1.32 مليار[3]تقديرات عام 2017ق. 30.8 مليون[4]مناطق الوجود المميزةبلد الأصل الهند البلد الهند الهند نيبال 4,000,000[5] الولايات المتحدة 3,982,398[6] الإمار...

Historic valley in Jerusalem and religious concept This article is about the valley located in Jerusalem, and the biblical term analogous to Christian Hades, Hell or Purgatory. For other uses, see Gehenna (disambiguation). GehennaGehinnomValley of HinnomGehennaLocation in Jerusalem, south of Mount ZionNamingNative nameגיא בן הינום (Hebrew)GeographyCoordinates31°46′6.3″N 35°13′49.6″E / 31.768417°N 35.230444°E / 31.768417; 35.230444 River...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

Culinary traditions of the United Kingdom Fish and chips, a popular take-away food of the United Kingdom Traditional pie and mash shop in London British cuisine National cuisines English Scottish Welsh Northern Irish Regional cuisines Carmarthenshire Monmouthshire Gower Pembrokeshire Ceredigion Cornwall Channel Islands Overseas/Fusion cuisine Anglo-Indian Anguillian Balti curries Bermudian British Chinese cuisine British Virgin Islands Cayman Islands Falkland Islands Gibraltarian Montserrat S...

American technology company Spansion Inc.IndustrySemiconductorsFounded2003DefunctMarch 12, 2015 (2015-03-12)FatePurchased by Cypress SemiconductorSuccessorCypress Semiconductor, later acquired by InfineonHeadquartersSunnyvale, California,United StatesKey peopleJohn Kispert (CEO and Member of Spansion's Board of Directors)ProductsFlash memory-based embedded systemsRevenue~$1.3 billion USD (Annual 2013)Number of employees~3,700 (2014)Websitewww.spansion.com Spansion Inc. was an A...

Supposed phenomena not subject to the laws of nature This article is about unexplained or non-natural forces and phenomena. For the television series, see Supernatural (American TV series). For other uses, see Supernatural (disambiguation). Supernatural power redirects here. For the popular culture concept of the imaginary superhuman abilities, see Superpower (ability). Saint Peter Attempting to Walk on Water (1766), painting by François Boucher Part of a series onAnthropology of religionTwo...

جيانغ كينغ (بالصينية: 江青) معلومات شخصية اسم الولادة (بالصينية: Lǐ Shūméng) الميلاد 19 مارس 1914(1914-03-19)تشوتشنغ [لغات أخرى][1]، والصين الوفاة 14 مايو 1991 (77 سنة)بكين سبب الوفاة إنتحار مواطنة الصين[2][3] جمهورية الصين (1914–1949) الديانة إلحاد عضوة في ...








