Факторизація многочленів
|
Read other articles:

The ArgusTypeWeekly newspaperFormattabloidOwner(s)Independent News & MediaEditorJohn Mulligan (Group Editor)Deputy editorJohn SavageFounded1830HeadquartersPark Street, DundalkWebsitewww.argus.ie The Argus is a regional newspaper serving Dundalk, Ireland. The paper is owned by Mediahuis, through its subsidiary Independent News & Media. The Argus is one of two non-free newspapers serving Dundalk, the other being the Dundalk Democrat. The newspaper is named after Argus Panoptes, a hundr...

Village in Essex, England All Saints' Church Wickham St Paul is a village and civil parish located five miles north of Halstead in the district of Braintree, Essex. The village, in which some of the houses surround a large open green (with cricket pitch and swings), contains a church, a public house, a part-time post office and a grocery store, part of a large farm shop and pick-your-own establishment.[1] The United Kingdom Census 2001 listed Wickham St Paul to have a population of 33...

2013 compilation album by B'zB'z The Best XXV 1999–2012Compilation album by B'zReleasedJune 12, 2013GenrePop rock, hard rockLabelVermillion RecordsProducerTak MatsumotoB'z chronology B'z The Best Ultra Treasure(2008) B'z The Best XXV 1999–2012(2013) B'z The Best XXV 1999–2012 is a compilation album by Japanese hard rock duo B'z. It was released on June 12, 2013, simultaneously with B'z The Best XXV 1988–1998, and it is part of their 25th anniversary celebration. It reached #2 ...

Hypargos Hyapargos margaritatus Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Aves Ordo: Passeriformes Famili: Estrildidae Genus: HypargosL. Reichenbach, 1862 Spesies Lihat teks Hypargos adalah salah satu genus burung pipit dalam familia Estrildidae. Genus ini memiliki 2 spesies yang ditemukan di sub-sahara Afrika. Spesies Hypargos niveoguttatus Hypargos margaritatus Pengidentifikasi takson Wikidata: Q785454 Wikispecies: Hypargos GBIF: 2493645 iNaturalist: 14043 IRMNG: 1274506...

Ini adalah nama Batak Toba, marganya adalah pasaribu. Daniel Pasaribu Wakil Kepala Kepolisian Daerah MalukuMasa jabatan2 Juni 2017 – 5 Januari 2018 PendahuluMusa GintingPenggantiHasanuddin Informasi pribadiLahir30 Juli 1962 (umur 61)Pematangsiantar, Sumatera UtaraAlma materAkademi Kepolisian (1985)Karier militerPihak IndonesiaDinas/cabang Kepolisian Negara Republik IndonesiaMasa dinas1985—2020Pangkat Inspektur Jenderal PolisiSatuanPendidikan PolriSunting kotak info...

American computer-animated fantasy film This article is about the film. For the video game, see Brave (video game). For the soundtrack, see Brave (soundtrack). BraveTheatrical release posterDirected by Mark Andrews Brenda Chapman Screenplay by Mark Andrews Steve Purcell Brenda Chapman Irene Mecchi Story byBrenda ChapmanProduced byKatherine SarafianStarring Kelly Macdonald Emma Thompson Billy Connolly Julie Walters Robbie Coltrane Kevin McKidd Craig Ferguson Cinematography Robert Anderson (cam...

Arabic variety spoken in Aleppo, Syria Aleppo ArabicAleppine ArabicArabic: اللهجة الحلبيةNative toSyriaLanguage familyAfro-Asiatic SemiticCentral SemiticArabicLevantine ArabicAleppo ArabicWriting systemArabic alphabetArabic chat alphabetLanguage codesISO 639-3(covered by apc)Glottologalep1241 North LevantineThis article contains IPA phonetic symbols. Without proper rendering support, you may see question marks, boxes, or other symbols instead of Unicode characters...

Weightlifting at the Olympics Women's 53 kgat the Games of the XXVII OlympiadVenueSydney Convention and Exhibition CentreDate18 SeptemberCompetitors10 from 10 nationsMedalists Yang Xia China Li Feng-ying Chinese Taipei Winarni Binti Slamet Indonesia2004 → Weightlifting at the2000 Summer OlympicsMenWomen56 kg48 kg62 kg53 kg69 kg58 kg77 kg63 kg85 kg69 kg94 kg75 kg105 kg+75 kg+105 kgvte Main article: Weightlifting at the 2000 Summer Olympics The women's 53 ...

Soccer match Football matchNASL Final 1973Texas Stadium hosted the FinalEventNASL Final Dallas Tornado Philadelphia Atoms 0 2 DateAugust 25, 1973 (1973-08-25)VenueTexas Stadium, Irving, TexasRefereeBill Gallacher (Canada)Attendance18,824← 1972 1974 → NASL Final 1973 was the championship match of the 1973 season, between the expansion Philadelphia Atoms and the Dallas Tornado. The match was played on August 25, 1973 at Texas Stadium in Irving, Texas. The Philadelphia...

هذه المقالة عن المجموعة العرقية الأتراك وليس عن من يحملون جنسية الجمهورية التركية أتراكTürkler (بالتركية) التعداد الكليالتعداد 70~83 مليون نسمةمناطق الوجود المميزةالبلد القائمة ... تركياألمانياسورياالعراقبلغارياالولايات المتحدةفرنساالمملكة المتحدةهولنداالنمساأسترالي�...

Ця стаття потребує додаткових посилань на джерела для поліпшення її перевірності. Будь ласка, допоможіть удосконалити цю статтю, додавши посилання на надійні (авторитетні) джерела. Зверніться на сторінку обговорення за поясненнями та допоможіть виправити недоліки. Мат...

خريطة لدوائر إقليم الناظور(صورة قديمة) دائرة الدريوش تقسيم إداري البلد المغرب التقسيم الأعلى إقليم الدريوش السكان التعداد السكاني 61068 (2004)[1] • عدد الأسر 10369 (2004)[1] تعديل مصدري - تعديل دائرة الدريوش هي إحدى الدائرتين المكونة لإقليم الدريوش وتتموق...

Национальное аэрокосмическое агентство Азербайджана Штаб-квартира Баку, ул. С. Ахундова, AZ 1115 Локация Азербайджан Тип организации Космическое агентство Руководители Директор: Натиг Джавадов Первый заместитель генерального директора Тофик Сулейманов Основание Осн�...

Canadian political controversy Conscription Crisis of 1917–1918An anti-conscription parade in Montreal on May 17, 1917Date1917–18LocationQuebecCaused byMilitary Service Act, ConscriptionGoals Repeal the Military Service Act End conscription in Canada MethodsMass protests, riotsResulted inParliament passes the Military Service ActParties Imperialists Prime Minister's Office Conservative Party Liberal–Unionists Ministry of Militia Nationalists His Majesty's Opposition Laurier Liberals Pac...

الخطوط الجوية الموزمبيقية إياتاTM إيكاوLAM رمز النداءMOZAMBIQUE تاريخ الإنشاء 26 أغسطس 1936 الجنسية موزمبيق موقع ويب الموقع الرسمي تعديل مصدري - تعديل الخطوط الجوية الموزمبيقية أو لام[1] (بالبرتغالية: LAM Linhas Aéreas de Moçambique) هي الناقل الوطني لموزمبيق.[2&...

El texto que sigue es una traducción defectuosa. Si quieres colaborar con Wikipedia, busca el artículo original y mejora esta traducción.Copia y pega el siguiente código en la página de discusión del autor de este artículo: {{subst:Aviso mal traducido|Billete de veinte dólares estadounidenses}} ~~~~ Billete de veinte dólares estadounidenses Anverso del billete de veinte dólares. Reverso del billete de veinte dólares.CaracterísticasValor facial 20 dólaresÁmbito Estados Uni...
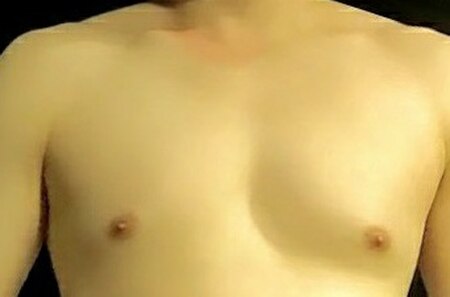
Region of the torso of a primate that in females serves as a mammary gland For other uses, see Breast (disambiguation). BreastMorphology of human female breasts with the areola, nipple, and inframammary foldHuman male breasts with defined pectoral musclesDetailsArteryInternal thoracic arteryVeinInternal thoracic veinIdentifiersLatinmamma (mammalis 'of the breast')[1]MeSHD001940TA98A16.0.02.001TA27097FMA9601Anatomical terminology[edit on Wikidata] The breast is one of two prominenc...

This article is about Windmill Hill, Hampshire. For other uses, see Windmill Hill. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Windmill Hill, Hampshire – news · newspapers · books · scholar · JSTOR (February 2021) (Learn how and when to remove this message) Windmill Hill viewed from the northwest Windmil...

La ScalafrazioneLa Scala – Veduta LocalizzazioneStato Italia Regione Toscana Provincia Pisa Comune San Miniato TerritorioCoordinate43°41′30.79″N 10°52′02.2″E43°41′30.79″N, 10°52′02.2″E (La Scala) Altitudine30 m s.l.m. Abitanti2 133[2] (2013) Altre informazioniCod. postale56028 Prefisso0571 Fuso orarioUTC+1 Nome abitantiscalese, scalesi[1] CartografiaLa Scala Modifica dati su Wikidata · Manuale La Scala è una f...

Diplomatic mission of Estonia to Russia Embassy of Estonia in Moscow (Russian: Посольство Эстонии в Москве, Estonian: Eesti Suursaatkond Moskvas) is the chief diplomatic mission of Estonia in the Russian Federation. It is located at 5 Maly Kislovsky Lane (Russian: Малый Кисловский пер. 5) in the Presnensky District of Moscow.[1] History The mansion was built in 1903, for the family of publisher Vladimir Dumnov.[2] In 1920, the mansion ...





























































